|
 |
| J Navig Port Res > Volume 47(6); 2023 > Article |
|
š š§
Š°¡ š¯õ瘚šŠ õçÙŠÇ š¯š ÚÇšÙ Úõý§ššš ÚÇšõçÚçõÇš šŠ¿šÊš õ¡¯š˜Ú š šŠ ÚÙš õ¯ õݯŠÎ˜ šýŠŠË¥ õ¯Š¯ÚšŠÊ. šŠÀšÇ ÚÙš õ¯ õݯŠÎ˜ šýŠŠ š Úçš š¥ŠÀ šš¿ šõ°šÇ õ¯š š š˜ŠŠË¥ š¡Àš ÚŠ Š¯ ÚšˋŠŠ Úš¯šÊŠŠËÇÚ õݯŠÎ˜(hausdorff distance)š Š ÚÙš õ¯š ŠšÏšŠ Ë(Speed Over Ground, SOG)š Úõñ õ¯š š¯´šÇ, õñ¡ŠÎ˜õ° ŠšÏš¿´ŠÀ(Course Over Ground)š ŠÑš¯ õ¯š š¯´šÇŠË¥ õ¯šÊÚˋÚš˜ šÊõ°ŠšŠÊ. šŠÀšÇ šýŠš š Ú´šÝš õýšÎÚõ¡¯ šÚš˜ šÊš AIS ÚÙš Š¯šÇÚ¯š Š°Úˋ õ篚ÏÚ šõ° ŠÎ˜šÎš ÚšˋÚ õ¡¯šÀÇ ÚÙš õ¯ õݯŠÎ˜ šýŠšš Š¿õç ŠÑššÇ šÚŠšš¥Šˋ¯, šŠÀšÇ õݯŠÎ˜ šýŠŠË¥ ÚšˋÚ ÚÙš õ篚ÏÚ õý¯õ°¥õ¯ Úš¯šÊŠŠËÇÚ õݯŠÎ˜(hausdorff distance), õñ¡ŠÎ˜õ° ŠÊšÇŠÇŠ₤¿ Úš šÚ õݯŠÎ˜(Dynamic Time Warping distance) ŠÝ õ¡¯šÀÇ šýŠš Š¿ÚÇ ÚÙš õ¯ šÏŠÎ˜š õݯŠÎ˜Š ŠšÏšŠ Š¯ ŠšÏš¿´ŠÀ ŠÝ š Š¯ õݯŠ Ú¿šÝš ŠÑÚ˜ŠË¥ Š¿šñÚõݯŠ õñ¡ šÇšš ššÊš¥ŠÀ š õçÚõý Š¯šÚõ° ššš Š¯šÇÚ¯ šõ¯ÚŠÀš´ Úš¡ÚšŠÊ. š Šš š¥ŠÀŠ Davies-Bouldin šÏÚŠË¥ õ¡¯šÊš¥ŠÀ, õ篚ÏÚ õý¯õ°¥õ¯ ŠšÝ š¯šÚõݯŠ š§õ¯ ŠÛš ššÊš õ¡¯ŠÀÚ ÚÚ¡, õݯŠÎ˜ õ°š¯ Ú´š´šÝššŠ Ú¿Ú š¯šÚ´š šÊšÎÚšŠÊ.
ABSTRACT
This study developed a new distance metric for vessel trajectories, applicable to marine traffic control services in the Korean coastal waters. The proposed metric is designed through the weighted summation of the traditional Hausdorff distance, which measures the similarity between spatiotemporal data and incorporates the differences in the average Speed Over Ground (SOG) and the variance in Course Over Ground (COG) between two trajectories. To validate the effectiveness of this new metric, a comparative analysis was conducted using the actual Automatic Identification System (AIS) trajectory data, in conjunction with an agglomerative clustering algorithm. Data visualizations were used to confirm that the results of trajectory clustering, with the new metric, reflect geographical distances and the distribution of vessel behavioral characteristics more accurately, than conventional metrics such as the Hausdorff distance and Dynamic Time Warping distance. Quantitatively, based on the Davies-Bouldin index, the clustering results were found to be superior or comparable and demonstrated exceptional efficiency in computational distance calculation.
š š¡õ° Š˜¥ŠŠšš ÚÇš šÇšÀšÇ ŠÇŠ¿ÚŠ Š¿š´šÇ 90%š šÀŠ¯Ú´š Š¯Š¥ ÚÇšÙ Ú¥šÀš Š¯ŠË¡ ÚÇš šš šÚš õý§õ¯Úõ¡¯ šÚš˜ ÚÇšÇ ŠÑš¥ššŠ š Š¯šŠšŠ°ššÊÚ
(AIS, Automatic Identification System)š¥ŠÀ šÀš Š¯ šš ŠŠ š Š¯ ÚÙš š Š°ÇŠË¥ ÚšˋÚ Š¯ˋŠýŠÀ õ¯Š¯š š õñ¿š š¥ŠÀ ŠšÚõ° šŠÊ(Zhao and Shi, 2019; Zhen et al., 2017). Ú¿Ú ŠÚš š¡ Š´¡š Š˜Š õ¡¯Šýš¡ ÚÙš õ篚ÏÚ Š¯ˋŠýŠÀ š õ¡¯Š¯š¥ŠÀ š š˜Ú š Š¯ŠÊš ššÏš, Ú¿š ŠÊš ÚÇš õçÚçššš š šŠ₤¡Ú Ú´ÚÇš Ú˜š¯ˋÚš˜ š Š¯ šÇÚÙ õ¯š Š¯ šš õÇš šŠ¿šÊ ŠÝš ÚšˋÚõ¡¯ šÚ š¯õç˜õ¯ ÚŠ¯ÚŠÊ(Zhao and Shi, 2019).
Ú¿Ú ÚÙõç˜ š¡õñ¥š ÚÇšÙš ÚÙŠÏ Š¯ Š˜¥ŠË ššÊš ŠÚ ššŠÀ š¡ÚÇ š¥Š¯š š¥ŠÀ Ú¥šÀŠõ¯ Šš¥Šˋ¯(Oh et al., 2018), ÚÙõ瘚 šÑš
ÚçŠÀõ¯ ŠŠ õçÙŠÇ š¯š, Ú¿Ú ÚÇšš šÇ Š°çšÀÚš˜ ÚÇšÙšÇ šÂš šŠ´ÚÇšššŠ Ú¥šÀŠ šÎõ¯š Š¯ŠË¡ šÑˋŠ, šÂšÇ ŠÝš ÚÇš˜ šš ŠÎ˜šÊÚ˜š ŠšÝ šñ´š§Ú šŠ¯š šŠÊ(Lee et al., 2010). Ú¿š ÚÇšÙššš Šš õçÚç Š¯šÏŠŠ š Š¯ šÑˋŠ ŠÝ šÏš š š¡ šš šÚš š¥õ¡¯Ú Š¢ šŠŠ¥, ÚÇšõçÚçõÇš š
Š˜Ç ŠÑÚŠË¥ Šš˜ šÚÚ õÇš šŠ¿šÊŠË¥ š ÚÇÚ š šŠÊ(Oh et al., 2018; Park and Park, 2022).
š Š¯ ÚÙš Š¯šÇÚ¯Š Š˜Çš Úçš ššÊÚ
š ÚçÚÇ šÊšõ¯š¥ŠÀ ššÏŠŠ ŠšˋŠ šš¿ šõ°šÇ Š¯šÇÚ¯šÇŠÊ. õñ¡ŠÎ˜õ° š Š¯ ÚÙš õ篚ÏÚŠ š š˜Ú ÚÙš ŠÊš ÚŠš õ篚Ϛ¥ŠÀ, šÇšÏš š¡ ÚÙš ŠÊš ŠÊŠË¡ õ篚Ϛ¥ŠÀ ÚŠ°ÚŠ õ°¥š šÇŠÊ. ŠÊšš š Š¯ ÚÙš ŠÊš ššš õ篚Ϛ¥ŠÀ šš§Úš˜ ÚÙš Š¯šÇÚ¯š šõ°¥ Š°çšÀšÝš šÊš¡ŠÊŠˋÇ, õÇš šŠ¿šÊ š
Š˜Ç ŠÑÚŠË¥ Ú˜õý õý§õ¯šÚÊõ° , š Š¯ šš šÇÚÙ ŠÎ˜šÊÚ˜ ŠÚ šÊš˜ õçÙŠÇ š¯š š Š¯š ÚÙÚ šš š õ° š õ¡¯š˜Ú š šš õýšÇŠÊ. Ú¿Ú ÚÙŠÏ š¡õñ¥š Š¿ŠÀ₤Ú õçÙŠÇš šÂš š¯š ÚÇšÙ Úõý§ššš ÚÇšÇ õçÚçŠšÇ šÎõ¯ÚŠ šÑš¡šš, õÇš š
Š˜Ç ŠÑÚš õý§õ¯ Ú´õ°¥Š ŠšÝ ÚÇ õýšÇŠÊ.
ŠÊŠÏ šÊš ÚÇš šš š õ¡¯š˜Ú š šŠ š Ú´Ú ÚÙš õ篚ÏÚŠË¥ šÚÇšŠ ÚÙš Š¯ š Š¯š Ú¿šÝš šÊš š š¥ŠÀ Š¯šÚ š š˜Š š¡Àš šýŠõ¯ š š ŠšÇš¥ ÚŠÊ. šÇŠ Š´šÚ šÏŠÎ˜š šš¿š õ¯õ¿šŠÏš¥ŠÀ ÚÙš õ¯ š š˜Šõ¯ š¡Àš Šõ¡¯Š°ÇŠÊŠ, Š¿šñÚ ÚǚٚǚNJ šÑš
ÚÙ Šˆˋš , š šÂ
, ÚÇšš ŠŠ š˜õ°¥š õݯŠÎ˜ ŠÝš Š¯ŠË¡ ŠÊšÚ Šš Ú¿šÝš š š˜šÝŠ Š¯šŠšÇš¥ Ú õýšÇŠÊ. ÚÙš š Š°Çš Šš š Š°ÇŠõ°¥ Š°çšÀšÝš Šˆ õ¯š ÚÙš õ篚Ï, ŠŠ õç¯šÏ ŠÇ ŠÚ ÚÙš š¥ŠÀš´ šÊšÇŠ, ÚÙš Š¯šÇÚ¯š šÏŠÎ˜š Š¯ Šš Ú¿šÝš Ú˜õÇÚš˜ š Ú´Úõý ÚÚÚŠ ÚÙš õ¯ š š˜Š šýŠõ¯ õ篚ÏÚ õ°¥š š õ¡¯šÊšÇ ŠŠÊŠˋÇ, õÇš šŠ¿šÊš ŠÑŠÇš šÊšÇŠˋÇšŠ š Š¯ Ú¿šÝš ŠÏŠ šš Ú ÚÙŠÀŠË¥ š õ°çÚŠ Š¯ õ¡¯š˜Ú š šš õýšÇŠÊ.
Š°¡ Š
¥Š˜¡ššŠ ÚÙš Š¯šÇÚ¯š õÇŠ ´Š õݯŠÎ˜ š¡Àš Š¯ˋŠýŠÀ õ°¥ õ篚ÏÚ šõ° ŠÎ˜šÎ ŠÝš õÇŠ ´Š õ¡¯šÀÇ š¯õ瘊ʚ š¯š šÇÚ¥õ° , õñ¡ šÝõ°¥ŠÊš š¯¡õ° Úš˜ Š ÚÙš õ¯š šÏŠÎ˜š õݯŠÎ˜Š¢ šŠŠ¥ ŠšÏšŠ Ë(SOG, Speed Over Ground)š Úõñ õ¯š š¯´šÇš Šš¿š¿´ŠÀ(COG, Course Over Ground)š ŠÑš¯ õ¯š š¯´šÇŠË¥ ÚšˋÚš˜ š Š¯ ÚÙš š Šš Ú¿šÝŠÊš Ú˜õÇš š¥ŠÀ Š¯šÚŠ šŠÀšÇ ÚÙš õ¯ õݯŠÎ˜ šýŠŠË¥ š šÚšŠÊ. šÇšÇš õ¯Š¯Ú š õñ õݯŠÎ˜ šýŠõ¯ õçÙŠÇ š¯š ÚÇšÙšš š Ú´Úõý ÚšˋŠ š šŠšÏŠË¥ šÊšÎÚõ¡¯ šÚš˜ õçÙŠÇ šÈ¥š ÚÙŠÏš šÑš
Ú šÊš š Š¯ ÚÙš Š¯šÇÚ¯ŠË¥ õ¡¯Š¯š¥ŠÀ ÚÙš õ¯ õݯŠÎ˜ õ°š¯ Š¯ ÚÙš õ篚ÏÚ õ°¥š š šÚÚšŠÊ. õñ¡ŠÎ˜õ° õ¡¯šÀÇ ÚÙš õ¯ õݯŠÎ˜ õ°š¯ šýŠš Š¿õçÚš˜ õ¯Š¯Š šýŠš õ¯š¿ŠË¥ Úõ¯Úõ¡¯ šÚš˜ šõ¯š Š¯ š Šš Š¯ˋŠýŠÀ š¥ŠÀ ŠÊšÚõý ŠÑšÚšŠÊ.
õ篚ÏÚ Ššš¡ š Š¯š ÚÙš š šõ¯š ڊΚ Š¯Š¥ šÚõ¯ Š°ÚŠ Šš š¡ õ¯šýÇš š Š°ÇŠË¥ ŠÇõ° šŠÊŠ Ú¿šÝšÇ ššÇ Š´š¥Ú šýŠŠÀš´ õñ¡ š š˜ŠŠË¥ š¡ÀŠÚõ¡¯õ¯ šÇŠ çŠÊ. šÇš Ú šš ÚÙš õ¯š š š˜Š, Ú¿š õñ¡ Š¯Š šýŠš¡ õݯŠÎ˜ŠË¥ ÚŠš šÊšŠÀ ÚÚÚõ¡¯ šÚ ŠÊšÚ š¡Àš Š¯ˋŠýŠÀ šÇ õ¯Š¯ŠšÇ šŠÊ(Buchin et al., 2012; Magdy et al., 2015).
š Š¯ ÚÙš W Š Ú¿š šš š š Š¯š šŠ Lat Š¯ õý§Š Lon šÂÚŠÀ ÚÚŠŠ šš¿ š Š°Ç, õñ¡ŠÎ˜õ° ŠšÏš¿´ŠÀ COG Š¯ ŠšÏšŠ Ë SOG ŠÝ õݯŠ š Š°ÇŠÀ ÚÚŠŠ š´šÇÚ˜š¡Ú¡(waypoints) wš šÏÚˋšÇŠÊ. šÇŠ š (1)õ°¥ õ¯šÇ š šÚ š šŠÊ.
šÎ, š Š¯š ÚÙš Š¯šÇÚ¯Š õ¡¯ŠÀŠ šš š Š¯Š¥ Š°ÚÚ š Š¯š šš¿ Š¯ Šš š Š°Çš šÑšÇŠË¥ š šËÚõ° šŠ šš¿ šõ°šÇ Š¯šÇÚ¯šÇŠÊ. š¥Š ´š š´šÇÚ˜š¡Ú¡ŠÀ õ瘚݊ ÚÙš š õ¡¯ÚÚš Ú¿šÝš Š¯šÚõݯŠ, Ú¿š šõ°šÇš Ú¿šÝš Š¯šÚ´š¥ŠÀš´ ÚÙš õ¯ õݯŠÎ˜Š ŠÊšõ°¥ õ¯šÇ š˜Š˜ Š¯ˋšš¥ŠÀ š šŠ š šŠÊ.
Úš¯šÊŠŠËÇÚ õݯŠÎ˜Š š˜Š˜ õ¥ÙšÏš š¥ŠÀ šÇŠÈ´šÇšÏ šŠÀ ŠÊŠË¡ Š šÏÚˋš õݯŠÎ˜ŠË¥ š¡Àš Úõ¡¯ šÚš˜ ÚšˋŠŠ Š¯ˋŠýŠÀ š¥ŠÀš, Š ÚÙš š õ¡¯ÚÚš š š˜ŠŠË¥ š¡Àš ÚŠÊ(Alt, 2009). Úš¯šÊŠŠËÇÚ õݯŠÎ˜ŠË¥ õç˜Úõ¡¯ šÚÇšŠ š¯š šŠÀ ŠÊŠË¡ ÚÙš š õ瘚ÝÚŠ Š õ¯š š´šÇÚ˜š¡Ú¡ŠÊš Šš š¥ŠÀ ÚŠ šçš õݯŠÎ˜ŠÊš Šˆ´Š õ°š¯ÚŠÊ. Úš¯šÊŠŠËÇÚ õݯŠÎ˜Š õñ¡ šçš õݯŠÎ˜ŠÊ šÊš šçŠõ¯šÇŠÊ. õ¯õ¯ š´šÇÚ˜š¡Ú¡ a, b š šÏÚˋš¥ŠÀ šÇŠÈ´šÇšÏ ÚÙš A, B õ¯ šš Š Š ÚÙš š Úš¯šÊŠŠËÇÚ õݯŠÎ˜ hausdorff(A,B)ŠË¥ ššš¥ŠÀ š šÚ õýšÇ š (2)šÇŠÊ.
ŠÊšÇŠÇŠ₤¿ Úš šÚ õݯŠÎ˜Š šŠÀ ŠÊŠË¡ Š õ¯š šõ°šÇ õ¯š õݯŠÎ˜ŠË¥ š¡Àš ÚŠ Š¯ ŠŠÎ˜ š˜šˋŠŠ Š¯ˋšš¥ŠÀ, Úš¯šÊŠŠËÇÚ õݯŠÎ˜ šýŠš š š˜Úõý šŠÀ ŠÊŠË¡ ÚÙš šš šÀÇš˜ÚŠ Š õ¯š š´šÇÚ˜š¡Ú¡ŠÀ õ¯ŠËÚ Šˆ´Š õݯŠÎ˜ šÀ¯Úˋš š˜õñš š¥ŠÀ õ°š¯ÚŠÊ(Keogh and Ratanamahatana, 2005). šÇŠ Š š´šÇÚ˜š¡Ú¡š šš š ššõ¯ š¥š¿ÚšÏ šŠŠ¥Š š´šÇÚ˜š¡Ú¡ õ¯š šçš š õݯŠÎ˜ŠË¥ ÚšÚŠ š¯š¯šÇ šÚŠŠ₤ŠÀ, šŠÀ ŠÊŠË¡ õ¡¡šÇš šõ°šÇ Š¯šÇÚ¯ õ¯š š š˜ŠŠË¥ š¡ÀŠÚ š šŠÊŠ šËš šÇ šš¥Š, š¯š¯ šš ŠÑŠÇšÇ Š¿õçš Ú˜ŠÊŠ Š˜¡š õ¯ šŠÊ(Magdy et al., 2015).
õ¯õ¯ š´šÇÚ˜š¡Ú¡ a, bŠÀ šÇŠÈ´šÇšÏ ÚÙš A, Bš ŠÊšÇŠÇŠ₤¿ Úš šÚ õݯŠÎ˜ DTW(A, B)ŠË¥ õç˜ÚŠ šš š (3)õ°¥ õ¯ŠÊ. šÇŠ Rest(A)Š šý¨ ŠýšÏ¡ š´šÇÚ˜š¡Ú¡ŠË¥ š š¡Ú ÚÙš Aš ÚÙš Š¯šÇÚ¯ŠË¥ šŠ₤¡ÚŠÊ(Magdy et al., 2015).
Úš¯šÊŠŠËÇÚ õݯŠÎ˜Š Š´šÚ š´šÇÚ˜š¡Ú¡š šŠ Š¯ õý§Š š Š°ÇŠÏš ÚšˋÚš˜ õ°š¯Š šÏŠÎ˜š õݯŠÎ˜ šýŠšÇŠ₤ŠÀ, š Š¯š ŠšÏšŠ Ë Š¯ ŠšÏš¿´ŠÀ š Š°ÇŠ Š¯šŠšÏ šŠŠÊ. šÇš Zhen et al.(2017)š Š ÚÙš õ¯š Úš¯šÊŠŠËÇÚ õݯŠÎ˜, õñ¡ŠÎ˜õ° ŠšÏš¿´ŠÀõ¯š š¯´šÇŠË¥ õ¯šÊÚˋš¥ŠÀ õý¯ÚˋÚš˜ šŠÀšÇ õݯŠÎ˜ šýŠŠË¥ õ° šÚšŠÊ.
Š°¡ š¯õ瘚šŠ ŠÊšÇŠÇŠ₤¿ Úš šÚ õݯŠÎ˜š Š¿ÚÇ Úš¯šÊŠŠËÇÚ õݯŠÎ˜õ¯ š¯š¯ š¡ÀŠˋÇšš ŠÑÚõ¯ š ŠÊŠ š , õñ¡ŠÎ˜õ° ÚÙš õ¯ šÏŠÎ˜š õݯŠÎ˜Š¢ šŠŠ¥ š Š¯š õݯŠ š Š°ÇŠË¥ ÚšˋÚš˜ ÚÙš š š š˜ŠŠË¥ Úõ¯Ú š šŠÊŠ š š š¯ˋšÚš˜, Zhen et al.(2017)š šýŠŠË¥ Š¯š šÚ´ ÚÚš ÚÙš õ¯ õݯŠÎ˜ Š¿õç Š¯ˋŠýŠÀ š õ¯Š¯ÚšŠÊ. Š°¡ š¯õ瘚š š šÚŠ ÚÙš õ¯ õݯŠÎ˜ š¡Àš Šýš ÚÙš õ¯š ŠšÏš¿´ŠÀš Úõñ õ¯ š¯´šÇõ¯ šŠ ŠÑš¯š š¯´šÇŠË¥ Š¯šÚ Š¢ŠÏ šŠŠ¥, ŠšÏšŠš Úõñ õ¯ š¯´šÇõ¿šÏ Š¯šÚš˜ š Š¯š õݯŠš šÂ
Úˋš š¥ŠÀ Š¯šÚŠ Š¯ˋŠýŠÀ šÇŠÊ.
šš š¡õ¡ÚšŠ₤šÇ ÚÙš õ¯ õݯŠÎ˜ ŠŠ š š˜ŠŠ ÚšˋÚŠ šýŠš õñ¥õݯښ˜ ŠÊšÚõý š šŠ š šš¥Šˋ¯, õ篚ÏÚ(Clustering) Šˆ´Š¡š Š¯ŠÀ šÇ õݯŠÎ˜ šýŠš õñ¥õݯښ˜ š š˜Ú õ¯šýÇŠÊš Šš¥ õ篚Ϛ¥ŠÀ Úõ¯ÚŠÊ. õ篚ÏÚ šõ° ŠÎ˜šÎš õ°çÚçš š¥ŠÀ ÚÇš˜ šš õ°¥ õÇŠ ´Š š Ú š¯õ瘊ʚšŠ ŠÊšš ÚÙš š õ篚Ϛ¥ŠÀ ŠÏŠÊšÇ õñ¡ š Š°ÇŠË¥ šš§Úõ¡¯ šÚ Šˆˋš š¥ŠÀ š˜šˋŠšš¥Šˋ¯, ÚšˋŠ šõ° ŠÎ˜šÎš ŠˆˋÚ õç¯šÏ õ¯šš¡ K õ¯š õç¯šÏ šÊš˜š š õ¯Ýš ÚÇõ¯Š Úšš K-means šõ° ŠÎ˜šÎš ÚšˋÚõݯŠ(Kim et al.,2014; Oh et al.,2018) Š¯Š õ¡¯Š¯š DBSCAN, HDBSCAN ŠÝšÇ šÈ¥ŠÀ ÚšˋŠšŠÊ(Rong et al.,2020; Dobrkovic et al.,2018; Pallotta et al.,2013).
Š°¡ š¯õ瘚šŠ šÏŠÎ˜š š¥ŠÀ Š°çšÀÚ õçÙŠÇ š¯ššš š Ú´Úõý ÚšˋŠ š šŠ ÚÙš õ¯ õݯŠÎ˜ š¡Àš Š¯ˋŠýŠÀ š õ¯Š¯Úõ° š ÚŠÊ. šÇš ÚÙš õ¯ šÏŠÎ˜š õݯŠÎ˜Š¢ šŠŠ¥ÚÙš š ÚÚ, š Š¯š Šš Ú¿šÝ ŠÝš Ú˜õÇš š¥ŠÀ Š¯šÚõ° šš (4)š õ¯šÇ Š ÚÙš õ¯š ŠšÏšŠ Ëš Úõñ õ¯š š¯´šÇ, õñ¡ŠÎ˜õ° ŠšÏš¿´ŠÀš ŠÑš¯ õ¯š š¯´šÇŠË¥ Úš¯šÊŠŠËÇÚ õݯŠÎ˜š õ¯šÊÚˋÚ š¯šš šÊõ°ÚšŠÊ.
Š ÚÙš š ŠšÏšŠ Ëš Úõñ õ¯š š¯´šÇŠ õ¯ ÚÙš š š Š¯ õ¯š š Š¯š š¡ šŠ š¯´šÇŠË¥ šŠ₤¡ÚŠˋ¯, šÇŠ š Š¯ ŠÚš š¡ Šš Ú¿šÝš ÚÇŠ¿ÚŠÊ. ÚÚ¡ Š ÚÙš š ŠšÏš¿´ŠÀš ŠÑš¯ õ¯š š¯´šÇŠ Š ÚÙš š šÏšÏšÝš š Š, šÎ ÚÙš š ÚÚš š¯´šÇŠË¥ Š¯šÚõ¡¯ šÚ ÚٚNJÊ. õ¯Š ¿ Š¯ˋÚËš Š°Úõ¯ š õݯŠ šÏšÏÚŠ ÚÙš š ŠšÏš¿´ŠÀš ŠÑš¯šÇ šš õýšÇŠˋ¯, Š°Úõ¯ Ú¯ ÚÙš š ŠÑš¯šÇ Ú˜ŠÊŠ õýš õ¯šÚ õýšÇŠÊ.
šŠÀÙõý š šŠ ÚÙš õ¯ õݯŠÎ˜ š¡Àš šýŠŠ ÚÙš õ¯ šÏŠÎ˜š õݯŠÎ˜š š Š¯š Šš Ú¿šÝ, õñ¡ŠÎ˜õ° ÚÙš ÚÚŠË¥ šÂ
Úˋš š¥ŠÀ Š¯šÚõ¡¯ šÚš˜ šÊõ°Š õýšÇŠÊ. šÇ õݯŠÎ˜ šýŠŠË¥ š šˋÚš˜ õ篚ÏÚ Ššš¡ ÚÙš ŠÊ š šýÇš ŠÚš˜ šŠÀ õ¯š õݯŠÎ˜õ¯ŠÊš õ°š¯ÚŠˋÇ, šÇ Šˆ´Š õݯŠÎ˜ š Š°ÇŠË¥ õݯŠÎ˜ ŠÏÊÚ¡ŠÎÙšÊ(distance matrix)š š šËÚ š šŠÊ. õݯŠÎ˜ ŠÏÊÚ¡ŠÎٚʚ õ¯ Ú ŠŠ šÇš õ¯ ÚÙš š ŠšŠŠ₤ŠÀ šÇŠ Šˆ´Š Šõ¯ ššš õ¯šÇ 0 š¡ Šš¿ÙÚŠ ˜(symmetric matrix)šÇŠÊ. õݯŠÎ˜ ŠÏÊÚ¡ŠÎٚʚŠ Šˆ´Š ÚÙš õ¯ õݯŠÎ˜ š Š°Çõ¯ š šËŠšÇ šš¥Š₤ŠÀ šÇŠË¥ šŠÀ õݯŠÎ˜õ¯ š š, šÎ š š˜Ú ÚÙš Š¥ŠÎ˜ õ篚ÏÚÚŠ šõ° ŠÎ˜šÎš ÚšˋŠŠÊ.
Š°Úˋ õç¯šÏ šõ° ŠÎ˜šÎš Š₤¡ŠÎ˜ ŠˆˋÚÚ õç¯šÏ õ¯šõ¯ Š˜šÝŠ Šõ¿šÏ š š˜Ú õç¯šÏŠÊšÇ š šÏš š¥ŠÀ Š Ú¯ õ篚Ϛ ÚšÝÚŠ šõ° ŠÎ˜šÎšÇŠÊ(Fisher, 1996).
šõ° ŠÎ˜šÎš šÇõ¡¯ šÊš ššŠ õ篚ÏÚ Šš, šÎ š šýÇ š Š¯ ÚÙš ŠÊšÇ Šˆ´Š šŠÀ ŠÊŠË¡ õ篚Ϛ¥ŠÀ õ¯šÈ¥ŠŠÊ. Š Ú¯ õ篚Ϛ ÚšÝÚõ¡¯ õç¯šÏ õ¯ š š˜ŠŠ, šš 3.1.šš š¡õ¡Š ÚÙš š šýÇš ŠÚ õݯŠÎ˜ ŠÏÊÚ¡ŠÎٚʊ˥ ÚšˋÚš˜ õ°š¯ŠŠÊ. õ篚ÏÚ šÏÚ šÊšŠ õç¯šÏ õ¯š õݯŠÎ˜, ŠŠ š š˜ŠŠË¥ õç¯šÏ ŠÇ ÚÙš ŠÊš õݯŠÎ˜š ŠÚ Úõñ õ¯š¥ŠÀ Úõ¯ÚŠŠÀ šÊš ŠŠˋ¯, õ篚Ϛ õ¯šõ¯ ŠˆˋÚ õç¯šÏ õ¯šŠ°ÇŠÊ ŠÏš õý§š¯, õ¯šË š š˜Ú õ篚ϊʚ Úˋš°õ¯Šˋ¯ šõ° ŠÎ˜šÎš šçšÂ
Š´õ°ššŠ ŠˆˋÚÚ õç¯šÏ õ¯šš Š¯Š¥ õ¯ ÚÙš ŠÊšÇ õ¯õ¯š õ篚Ϛ šÚõý ŠŠÊ.
Š°¡ š¯õ瘚šŠ šŠÀšÇ ÚÙš õ¯ õݯŠÎ˜ šýŠš š Ú´šÝš ŠÑšÚõ¡¯ šÚš˜ Š°Úˋ õç¯šÏ šõ° ŠÎ˜šÎš ŠÑš Šš ÚÙš ŠÊš š šˋÚ õý¯õ°¥ŠË¥ ÚšˋÚšŠÊ. šŠÀšÇ šýŠŠË¥ õ¡¯šÀÇ šýŠš Š¿õçÚš˜š¥ ÚŠ₤ŠÀ Šš¥Ú ŠˆˋÚ õç¯šÏ õ¯šŠË¥ šÊš Úšš¥Šˋ¯, õç¯šÏ ŠÇ ŠŠ õç¯šÏ õ¯ Ú¿šÝš Úš¡Úš˜ õñ šÏÚ Ú¿šÝš ÚÙš ŠÊšÇ Šš¥ õ篚Ϛ¥ŠÀ Ú˜š¯ˋŠšŠšÏ, Ú¿š šÇšÏš š¡ ÚÙš ŠÊšÇ õ¯õ¯ ŠÊŠË¡ õ篚Ϛ¥ŠÀš Úõ¯ŠšŠšÏŠË¥ ŠÊšÚ Š¯ˋšš¥ŠÀ ŠÑšÚšŠÊ.
Š°¡ š¯õ瘚šŠ AIS ŠÀ ššÏŠ š Š¯ ÚÙš Š¯šÇÚ¯ŠË¥ ÚšˋÚš˜ õçÙŠÇ ÚÇšÙššš š Š¯ ÚÙš õ篚ÏÚš š ÚˋÚ õݯŠÎ˜ š¡Àš Š¯ˋŠýŠÀ š õ¯Š¯Úõ° õýšÎÚšŠÊ. š (1)šš š šÚšŠ₤šÇ ÚÙš Š¯šÇÚ¯Š AIS Úçš ššÊÚ
š¥ŠÀ šÊšõ¯š¥ŠÀ ššÏŠŠ šŠ Š¯ õý§Š, ŠšÏš¿´ŠÀš ŠšÏšŠ Ë ŠÝš š Š°ÇŠË¥ ŠÇõ° šš¥Šˋ¯, õ¯ š Š¯š ŠÚ šŠ° š Š°ÇŠ šÚ¡ÚŠšÇ šŠÊ. ŠÊŠÏ Šš¥Ú š Š¯ šŠ°šŠ¥ŠˋÇ šÚ¡ÚŠ šŠ° š Š°ÇŠ Šš¥Ú õ¯š õ¯šÏõ¡¯ ŠŠ˜¡š õ¯ š´šÇÚ˜š¡Ú¡ŠÊšÇ Šš¥ š Š¯š ÚÙš š¡šÏŠË¥ ÚŠ´ÚŠ õýšŠ Š˜¡š õ¯ ššŠÊ. õñ¡ Š¯š õ瘚ýÇš š¡ šÊÚ Úõý§š šÇÚ šš¡Ú šÊÚ Š¯ õ° š¯¯ ŠÑŠÑšš ŠÊŠÈ˜ŠÊ.
ÚÙÚ šÊš¡ š Š¯š ÚÙš ŠÊš Ššš¥ŠÀ ÚÙš õ¯ õݯŠÎ˜ŠË¥ š¡Àš Úõ° õ篚ÏÚŠË¥ šÏÚÚõ¡¯ šÚš˜, šŠ Š¯ õý§Š õ¯šš šÇšš¿õ¯ šŠ ÚÙš š š š¡ÚšŠÊ. šš¡Š˜ šçŠ šŠ ËšÇ 2knots(3.7km/h) šÇÚš¡ ÚÙš š š šÏÚ š Š¯š ÚÙš Š¯šÇÚ¯ŠÀ õ¯šÈ¥Úš˜ ŠÏš¯˜õ¯šÏŠÀ Šˆ´Š ŠÑš Šš Š¯šÇÚ¯šš š š¡ÚšŠÊ.
š (4)š õ¯šÇ šš¿ š Š°Çš š Š¯ Šš š Š°ÇŠË¥ õý¯ÚˋÚš˜ š šŠ šŠÀšÇ õݯŠÎ˜ šýŠŠË¥ šÊš ÚÙš Š¯šÇÚ¯š š šˋÚŠ ÊŠˋÇ õ¯ Ú¿šÝš Šýš Š¯ Š´š š¯´šÇŠË¥ õ° Š ÊÚš˜ š õñÚÚš˜š¥ ÚŠÊ. Šš ÚÙš Š¯šÇÚ¯š šŠ Š¯ õý§Š, ŠšÏšŠ Ëš ŠÚÇšŠ šçšõ¯š 0, šçŠõ¯š 1 ŠÀ ŠÏÊÚÚš˜ š õñÚÚšš¥Šˋ¯, õ¯Šš¡ ŠšÏš¿´ŠÀŠ š˜š¡(sine) Ú´šŠË¥ ÚšˋÚš˜ ŠÏš¯˜õ¯šÏŠÀ 0 õ°¥ 1 š˜šÇš õ¯š¥ŠÀ š õñÚÚšŠÊ.
Š°¡ š¯õ瘚šŠ õ¯Š¯Ú šŠÀšÇ õݯŠÎ˜ šýŠš õ¯š¿ŠË¥ õýšÎÚõ¡¯ šÚš˜, š õñ õݯŠÎ˜ šýŠ Š¯ õ¡¯šÀÇš õݯŠÎ˜ šýŠŠÊ õ¯õ¯š Š¯ˋŠýš¥ŠÀ õ°š¯Š õݯŠÎ˜ ŠÏÊÚ¡ŠÎٚʚ Šš¥Ú Š°Úˋ õ篚ÏÚ šõ° ŠÎ˜šÎš š šˋÚš˜ õñ¡ õý¯õ°¥ŠË¥ Š¿õçÚŠ šÊÚš šÚÚšŠÊ.
šš 3.1 šš šš ÚšŠ₤šÇ, Š°¡ š¯õ瘚šŠ ÚÙš š ÚÚš š Š¯š Šš Ú¿šÝš š¯´šÇ, õñ¡ŠÎ˜õ° ÚÙš õ¯ šÏŠÎ˜š õݯŠÎ˜ŠË¥ Š¯šÚ õݯŠÎ˜ šýŠŠË¥ õ° šÚšŠÊ. šÇ õݯŠÎ˜Š š (4)š õ¯ ÚÙš ŠÑš˜ŠŠ õ¯šÊš¿ šÀ¯Úˋš šÚÇ ŠÊšÚõý š šŠ š šŠÊ. ÚÙš õ篚ÏÚ õ°¥š š ŠÑš Šš š šýÇ ÚÙš ŠÊ õ¯š õ¯ŠËÚ Šˆ´Š õݯŠÎ˜š ŠÚ õ¯š š šËÚ õݯŠÎ˜ ŠÏÊÚ¡ŠÎٚʚ õ¡¯Š¯Úš˜ šÇŠÈ´šÇšÏŠÊ. šÎ, ÚÙš š õ¯šõ¯ ŠÏššÏšŠÀ õݯŠÎ˜ ŠÏÊÚ¡ŠÎٚʊ˥ ššÝÚŠ Š¯ ŠŠ š¯š¯Šš š õ°Ýš¥ŠÀ šÎõ¯ÚŠˋ¯, Šš ÚÙš õ¯šõ¯ Šš¥ÚŠŠ¥Š š šŠŠ ÚÙš õ¯ õݯŠÎ˜ šýŠõ¯ ŠšÇŠŠˋÇ õ°š¯Úš˜š¥ ÚŠ õݯŠÎ˜ ŠÏÊÚ¡ŠÎٚʚ šŠ õñ¡š Š¿ŠÀÚš˜ ŠšÇŠ õýšÇŠÊ. õñ¡Š˜Š₤ŠÀ õ¡¯šÀÇ ÚÙš õ¯ õݯŠÎ˜ šýŠš šŠÀšÇ õݯŠÎ˜ šýŠŠË¥ Š¿õçÚŠ šÊÚ šÇš š, šŠÀšÇ õݯŠÎ˜ šýŠŠË¥ ÚŠŠÀ š šÚ š šŠ šçš š õ¯šÊš¿ šÀ¯Úˋš Úš¡Úõ¡¯ šÚ šÊÚšÇ š ÚŠ õýšÇŠÊ.
õ¡¯šÀÇ ÚÙš õ¯ õݯŠÎ˜ šýŠš Š¿õçÚš˜ šŠÀšÇ õݯŠÎ˜ šýŠš š Ú´šÝš õýšÎÚŠ šÊÚššŠ šÊš ÚÙš Š¯šÇÚ¯š ŠÚÇ Úš¯šÊŠŠËÇÚ õݯŠÎ˜š ŠÊšÇŠÇŠ₤¿ Úš šÚ õݯŠÎ˜, õñ¡ŠÎ˜õ° š ÚŠ šÊÚšš Š¯õý˜Š šçš š õ¯šÊš¿ šÀ¯Úˋš¥ŠÀ š šŠ šŠÀšÇ õݯŠÎ˜ ŠÝ šÇ š¡ õ¯šÏ õݯŠÎ˜ šýŠš õ¡¯Š¯Ú õ篚ÏÚ õý¯õ°¥ŠË¥ ŠÊšÚ š¡ÀŠˋÇšš Š¿õçÚšŠÊ. š¯š õ¯ šýŠš õ¡¯Š¯Ú õݯŠÎ˜ ŠÏÊÚ¡ŠÎÙšÊõ¯ š¥ŠÏŠ š šÚõý õ°š¯ŠŠšÏŠË¥ Š¿õçÚ´š¥ŠÀš´ š¯š¯ š¡ÀŠˋÇššš Ú´š´šÝš Š¿õçÚšŠÊ. šÇšÇš š¡ õ¯šÏ õݯŠÎ˜ ŠÏÊÚ¡ŠÎٚʚ Šš¥ õ篚ÏÚ šõ° ŠÎ˜šÎš š šˋÚ õý¯õ°¥ŠË¥ š Šš šýŠ, õñ¡ŠÎ˜õ° õ篚ϊ° ÚÙš Š¯šÇÚ¯š Ú¿šÝŠ° ŠÑÚ˜ŠË¥ Úš¡Ú š šŠ šõ¯Ú Š¯ˋŠýŠÀ š ÚšˋÚš˜ Š¿õçÚšŠÊ.
ÚÙš Š°Úˋ õ篚ÏÚ šõ° ŠÎ˜šÎš šÀ¯õÝÇš Šˆ´Š šÊÚšš Šš¥Úõý š šˋŠšŠÊ. šçšÂ
õç¯šÏ õ¯šõ¯ 5 õ¯õ¯ Š Šõ¿šÏ š š˜Ú õ篚Ϛ Š°ÚˋÚŠŠÀ šÊš Ššš¥Šˋ¯, õ篚Ïõ¯ š š˜ŠŠ šŠÀ ŠÊŠË¡ õ篚Ϛ šÚŠ Š ÚÙš õ¯ õݯŠÎ˜õ¯ŠÊš Úõñ õ¯š¥ŠÀ õ°š¯ŠšŠÊ.
õ篚ÏÚ õý¯õ°¥š ŠÚ š Šš Úõ¯Š õç¯šÏ ŠÇ Š°Š Š¯ õç¯šÏ õ¯ š š˜ŠŠË¥ šÏõÇš š¥ŠÀ š¡Àš ÚŠ Davies-Bouldin šÏÚ(DB)ŠË¥ ÚšˋÚŠˋ¯, šÇŠ šÇ Nõ¯š õ篚Ϛ ŠÚÇ õç¯šÏ iš õç¯šÏ jš ŠÚ šÊš˜š (centroids) c š˜šÇš š ÚNJΘŠš¡ õݯŠÎ˜(Euclidean distance)ŠÀ š šŠ õç¯šÏ õ¯ õݯŠÎ˜ M š ŠÑŠˆ´ŠÀ Úõ° , õç¯šÏ ŠÇ šÊš˜š ŠŠ¿ ÚÙš š´šÇÚ˜š¡Ú¡ X ŠÊš Š°ŠšÝš¥ŠÀ š šŠ S ŠË¥ ŠÑšŠÀ ÚŠ šÏÚ R ŠÀš´ š (5)š õ¯šÇ š šŠŠÊ(Davies and Bouldin, 1979). šÎ, õç¯šÏ ŠÇ Š°ŠšÝš šõ° , õç¯šÏ õ¯ õݯŠÎ˜Š ŠˋŠŠÀ š õ篚ÏÚŠšÇ šš¥ŠˋÇ Davies-Bouldin šÏÚš õ¯š šššÏŠÊ.
š˜šÇ ŠÏõ° ÚÇšš šÇ Š°çšÀÚ õçÙŠÇ š¯š Úõý§ššš š Ú´šÝš šÊšÎÚõ¡¯ šÚš˜, 2022 Š
11 š õ¯ šŠ´ÚÇšš šÈ¥š ÚÙõ瘚 š
ÚÙÚŠ Š¿šÇš š Š¯ŠÊš šÊš ÚÙš ŠÊšÇ šÊÚšš ÚšˋŠšŠÊ.
šŠÀšÇ ÚÙš õ¯ õݯŠÎ˜ŠË¥ š šÚ šçš š õ¯šÊš¿ šÀ¯Úˋš ÚšÚõ¡¯ šÚš˜, 2022 Š
11 š õ¯ Ú˜ÚÙÚÙšš šÑÚÙÚš˜ õÇšÚÙš š
ÚÙÚ Š¿šÇš š Š¯ŠÊš 37 õ¯š ÚÙš ŠÊš Ššš¥ŠÀ, š¡ õ¯šÏš õ¯šÊš¿ šÀ¯Úˋš¥ŠÀ õ°š¯Ú ÚÙš õ¯ õݯŠÎ˜ ŠÏÊÚ¡ŠÎٚʊ˥ õ¡¯Š¯š¥ŠÀ õ篚ÏÚŠË¥ šÚÚšŠÊ. õ¯šÊš¿ šÀ¯Úˋ 1 š Úš¯šÊŠŠËÇÚ õݯŠÎ˜õ¯šÇ šŠ ÚÙš õ¯šË Ú¯ õ¯šÊš¿š¡ 0.5 ŠË¥ Šõ° , õñ¡ š¡š ÚÙššŠ 0.25 ŠÀ õñ ŠÝÚõý õ¯šÊš¿ŠË¥ ŠÑš˜Ú šÀ¯ÚˋšÇŠÊ. Š¿šñÚ Š¯ˋšš¥ŠÀ šÀ¯Úˋ 2 Š š Š¯ õ¯ Úõñ ŠšÏšŠ Ëš š¯´šÇ, õñ¡ŠÎ˜õ° šÀ¯Úˋ 3 š ŠšÏš¿´ŠÀš ŠÑš¯š õ¯šË Ú¯ õ¯šÊš¿ŠË¥ ŠÑš˜ÚšŠÊ.
Fig. 1 š a), b), õñ¡ŠÎ˜õ° c)Š õ¯õ¯ õ¯šÊš¿ šÀ¯Úˋ 1, šÀ¯Úˋ 2, õñ¡ŠÎ˜õ° šÀ¯Úˋ 3 š š šˋÚš˜ ÚÙš ŠÊš ŠÊš₤ õ¯š õ篚Ϛ¥ŠÀ ŠÏŠÊšÇ õ¯š õ篚Ϛ Šš¥Ú šš¥ŠÀ ÚÙš š š´šÇÚ˜š¡Ú¡ŠÊš šÏŠšš ÚšÚ õý¯õ°¥šÇŠÊ. šÏŠÎ˜š š Š°Çš ÚÙš š ÚÚŠË¥ õ¡¯šÊš¥ŠÀ õÇšÚÙš¥ŠÀ š õñ¥ÚŠ ÚÙš ŠÊš š˜õ°¥ Š¿õçš õ¯õ¿šÇ ÚÙš , õñ¡ŠÎ˜õ° Š´¥ Š¯ŠÊŠÀŠÑÚ¯ š õñ¥ÚŠ ÚÙš Ú˜õý Š õ¯šÏŠÀ ŠÑõ¡¯ŠŠˋ¯, š¡ õ¯šÏ šÀ¯Úˋš õ篚ÏÚ õý¯õ°¥õ¯ š Š¯š š¥ŠÀ õñ¡Š˜Ú ÚÙš š ÚÚ š¯´šÇŠË¥ Š¯šÚõ° ššš Úš¡Ú š šŠÊ.
ÚÙš š ÚÚŠ šš¿ š Š°Ç š¡šŠ š Š¯š õݯŠ õÇŠ ´ š Š°Çõ¯ õ篚ÏÚš Š¯šŠŠšÏ ŠÑšÚõ¡¯ šÚš˜ õ¯ õ篚Ϛ šÚŠ ÚÙš ŠÊš Úõñ ŠšÏš¿´ŠÀõ¯õ°¥ Úõñ ŠšÏšŠ Ëš ŠÑÚ˜ŠË¥ Úš¡ÚšŠÊ. Fig. 2 š a), b), õñ¡ŠÎ˜õ° c)Š õ¯õ¯ õ¯šÊš¿ šÀ¯Úˋ 1, šÀ¯Úˋ 2, õñ¡ŠÎ˜õ° šÀ¯Úˋ 3 š¥ŠÀ ÚÙš õ¯ õݯŠÎ˜ŠË¥ š šÚõ° , õ¯ õç¯šÏ ŠÇ ÚÙš ŠÊ õ¯õ¯š š õñÚŠ ŠšÏš¿´ŠÀõ¯š Úõñ õ¯ŠÊ, õñ¡ŠÎ˜õ° ŠšÏšŠ Ëš Úõñ õ¯ŠÊ ŠÑÚ˜ŠË¥ Š¯šÊ ÚŠÀ₤(box plot)š¥ŠÀ šõ¯ÚÚ õýšÇŠÊ. õ¯õ¯š šõ¯Ú šŠÈšš, Š¯šÊš ŠšÇõ¯ šÏÏššŠÀ ÚÇŠ¿ õ篚ϚšŠ Úõñ š¥ŠÀ ŠÚŠŠ š Š¯ õݯŠš õý§ÚËšÝšÇ Š¿õçš õñ šÏÚ ÚÙš ŠÊšÇ Š˜ÑšŠÊõ° ÚÇšÚ š šŠÊ. Š, õ¯ õ篚Ϛ Š¯šÊš ŠšÇõ¯ õ¯õ¯ ŠÊŠË¡ Šýšš õÝ¡š° šŠÊŠˋÇ, ÚÇŠ¿ õ篚ÏÚ õý¯õ°¥Š šÇšÏš š¡ Ú¿šÝš šÏŠ ÚÙš ŠÊš ŠÊŠË¡ õ篚Ϛ¥ŠÀš š ŠÑŠËÚšŠÊõ° ÚÇšÚ š šŠÊ.
š¡ õ¯šÏ õ¯šÊš¿ šÀ¯Úˋ Šˆ´Ššš š Š¯š ŠšÏš¿´ŠÀ, õñ¡ŠÎ˜õ° ŠšÏšŠ Ë ŠÑÚ˜š š¯´šÇŠË¥ Ú´õ£ õ¯šÚŠˋÇ õ篚ϊ°ŠÀ š¯´šÇõ¯ Úš¡ŠŠÊ. ŠÊŠÏ, õ¯šÊš¿ šÀ¯Úˋ 1 ššŠ ÚÙš ŠšÏšŠ ËŠ¢ šŠŠ¥ ŠšÏš¿´ŠÀš ŠÑÚ˜ššŠ õ篚ϊ° š¯´šÇõ¯ Šˆ
ÚÚõ° , õç¯šÏ ŠÇ õ¯ šš¿š ŠÑš¯šÇ ŠÊŠË¡ šÀ¯Úˋš Š¿ÚÇ šŠÊŠ š šÇ Úš¡ŠŠÊ. ŠÚ Table 1 šš Úš¡Ú š šŠ₤šÇ, Davies-Bouldin šÏÚŠË¥ ÚšˋÚ š Šš õ篚ÏÚ Úõ¯ šýŠššŠ, õ¯šÊš¿ šÀ¯Úˋ 1 š šÏÚŠ 4.88 ŠÀ, ŠÊŠË¡ šÀ¯Úˋš 7.5 ŠŠ 7.7 š Š¿ÚÇ õ¯šÇ ŠÛŠÊŠ õýš š š šŠÊ. šÇŠ˜Ú õý¯õ°¥ŠË¥ šÂ
ÚˋÚš˜, Š°¡ š¯õ瘚š š šÚ šŠÀšÇ ÚÙš õ¯ õݯŠÎ˜ šýŠŠË¥ šçš š¥ŠÀ š šÚŠ šÀ¯Úˋš¥ŠÀš õ¯šÊš¿ šÀ¯Úˋ 1 š š ÚÚšŠÊ.
ÚÙŠÏš š õñ¥ÚŠ šÊš š Š¯ ÚÙš š ÚšˋÚ š ÚŠ šÊÚš ÚçÚÇ šŠÀšÇ ÚÙš õ¯ õݯŠÎ˜ šýŠŠË¥ š šÚõ¡¯ šÚ šçš š õ¯šÊš¿ šÀ¯Úˋš Úš¡ÚšŠÊ. ŠÏš¯˜õ¯šÏš Š¯ˋšš¥ŠÀ õ¡¯šÀÇ ÚÙš õ¯ õݯŠÎ˜ š¡Àš Š¯ˋš ŠŠ¿ Š°¡ Š
¥Š˜¡šš š šÚŠ šŠÀšÇ šýŠš š Ú´šÝš šÊšÎÚõ° š 2022 Š
11 š õ¯ š šÈ¥ÚÙšš šÑÚÙÚš˜ ŠˆˋÚ˜ÚÙš š
ÚÙÚ Š¿šÇš š Š¯ŠÊš 242 õ¯š ÚÙš ŠÊš Ššš¥ŠÀ š¡ õ¯šÏš õݯŠÎ˜ š¡Àš Š¯ˋšš¥ŠÀ õ°š¯Ú õݯŠÎ˜ŠË¥ õ¡¯Š¯š¥ŠÀ õ篚ÏÚŠË¥ šÚÚšŠÊ. šÎ, Úš¯šÊŠŠËÇÚ õݯŠÎ˜, ŠÊšÇŠÇŠ₤¿ Úš šÚ õݯŠÎ˜, õñ¡ŠÎ˜õ° š (6)š õ¯šÇ õ°š¯ŠŠ šŠÀšÇ õݯŠÎ˜ŠË¥ š šˋÚš˜ õ¯õ¯š õݯŠÎ˜ ŠÏÊÚ¡ŠÎٚʊ˥ õ°š¯Úõ° , Šš¥Ú õ篚ÏÚ šõ° ŠÎ˜šÎš š šˋÚŠ õ°¥š š ŠÊšÚ õÇš šš Š¿õç ŠÑšÚšŠÊ.
š¯š Table 2 ššŠ ÚÙš õ¯ õݯŠÎ˜ šýŠŠ° õݯŠÎ˜ ŠÏÊÚ¡ŠÎٚʊ˥ õ°š¯ÚŠ Š¯ ššŠ š¯š¯ šõ¯š Úš¡Ú š šŠÊ. Šš¥Ú ÚÙš Š¯šÇÚ¯š ŠÚÇ Úš¯šÊŠŠËÇÚ õݯŠÎ˜, õñ¡ŠÎ˜õ° šŠÀšÇ õݯŠÎ˜ šýŠššŠ õݯŠÎ˜ ŠÏÊÚ¡ŠÎÙšÊ š¯š¯šÇ š§ 249 šÇ š Šõ¯ ššŠŠ, ŠÊšÇŠÇŠ₤¿ Úš šÚ õݯŠÎ˜š ŠÚÇšŠ õñ¡Š°ÇŠÊ 2 ŠÑ šÇššÇ Š ššŠ š§ 374 šÇõ¯ õ¡¯ŠÀŠšŠÊ. šÇŠ Š¿õçš š¯š¯ŠšÇ ŠÏŠÊŠ ŠÊšÇŠÇŠ₤¿ Úš šÚ õݯŠÎ˜š ŠÚ Š´š š šÏš Ú õ¡¯šÀÇ š¯õ瘊Êõ°¥ š¥š¿ÚŠ õý¯õ°¥šÇŠÊ(Magdy et al., 2015).
Fig. 3 š a), b), õñ¡ŠÎ˜õ° c)Š õ¯õ¯ õ¯šÊš¿ Úš¯šÊŠŠËÇÚ õݯŠÎ˜, ŠÊšÇŠÇŠ₤¿ Úš šÚ õݯŠÎ˜, õñ¡ŠÎ˜õ° šŠÀšÇ õݯŠÎ˜ šýŠŠË¥ š šˋÚ õ篚ÏÚš õý¯õ°¥šÇŠÊ. Fig. 1 õ°¥ ŠÏš¯˜õ¯šÏŠÀ, Šš¥Ú õ篚Ϛ Šš¥Ú šš š´šÇÚ˜š¡Ú¡ŠÊŠÀ šÏŠšš ÚšŠšŠÊ. Fig. 3 š a)šš ŠÚŠŠ₤šÇ, Úš¯šÊŠŠËÇÚ õݯŠÎ˜ŠË¥ ÚšˋÚ õ篚ÏÚ õý¯õ°¥Š õݯš Šˆ´Š ÚÙš ŠÊš õ¯š õ篚Ϛ¥ŠÀ ÚŠ´Ú õýš š š šŠÊ. ÚÚ¡ ŠÊšÇŠÇŠ₤¿ Úš šÚš š šˋÚ b)Š a)š Š¿ÚÇ šÂ Š š õçÚ õ篚ÏÚ õý¯õ°¥ŠË¥ Š°Çš˜šÈ¥õ° šŠÊ. Ú¿Ú ÚÇŠ¿ õý¯õ°¥ššŠ Š¿õçš ÚÇšš š õñ¥š Ú ÚÙš ŠÊš š˜Ú ŠÊŠË¡ ÚÙš õ°¥Š ŠÊŠË¡ õ篚Ϛ¥ŠÀ õ°š¯Š õýš š š šŠÊ. ÚÚ¡ c)Š šš Úš¡Ú a)š b)š õ篚ÏÚ õý¯õ°¥š Š¿õçÚš˜ Ú¿Ú Š´¥ Š¯ŠÊšš š
ÚÙÚŠ ÚÙš ŠÊš ŠÚÇ šÂ Š ŠÊšÚõý õ篚ÏÚÚ õý¯õ°¥ŠË¥ Š°Çš˜šÈ¥õ° šŠÊ.
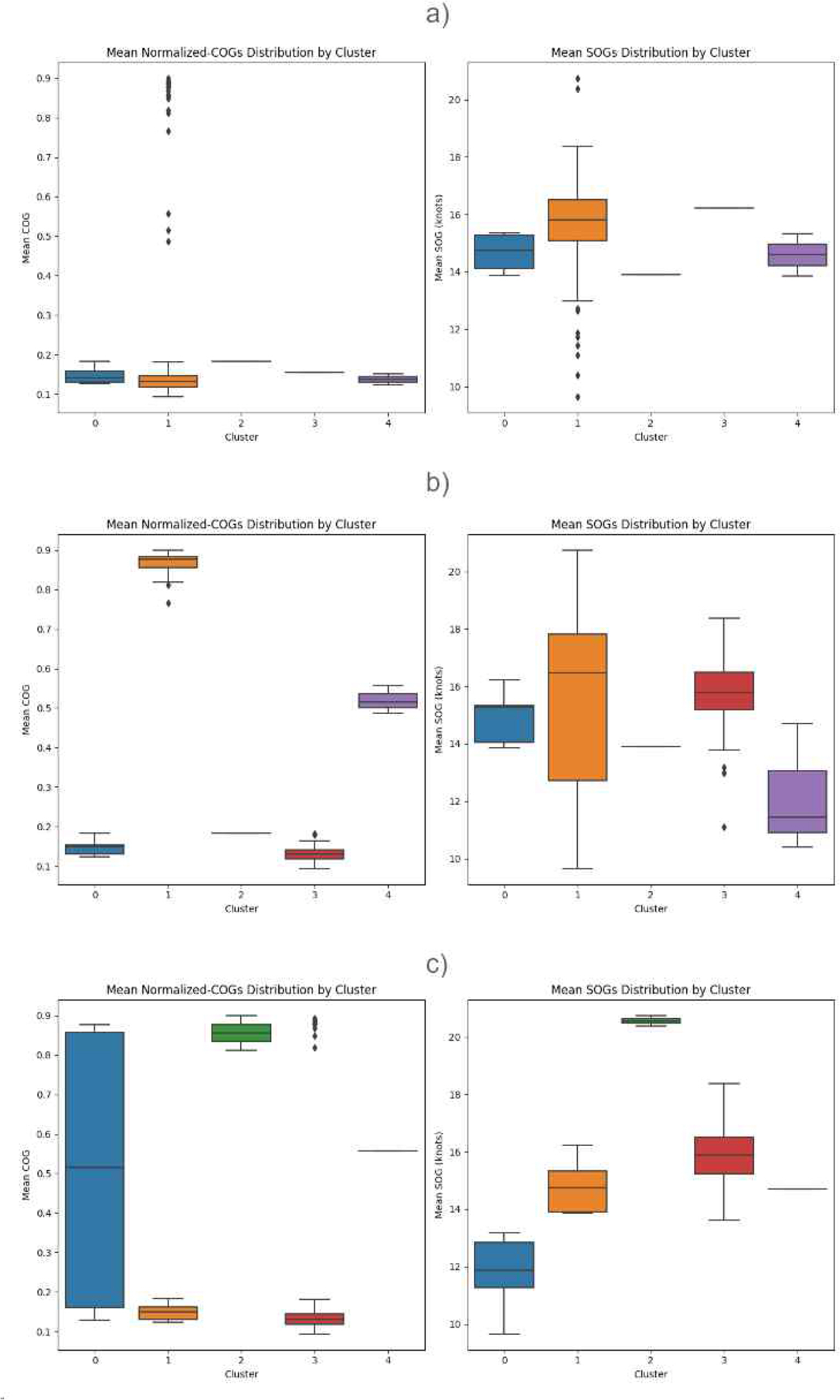
5.1.õ°¥ ŠÏš¯˜õ¯šÏŠÀ õ¯ õݯŠÎ˜ šýŠš õ¡¯Š¯Ú ÚÙš õ篚ÏÚ õý¯õ°¥õ¯ š Š¯Š° õݯŠ š Š°ÇŠË¥ Š¯šÚšŠšÏ Úš¡Úõ¡¯ šÚš˜, Fig. 4 õ°¥ õ¯šÇ õ篚ϊ° ÚÙš ŠÊš Úõñ ŠšÏš¿´ŠÀõ¯õ°¥ Úõñ ŠšÏšŠ Ëš ŠÑÚ˜ŠË¥ Úš¡ÚšŠÊ. Fig. 4 š a)Š Úš¯šÊŠŠËÇÚ õݯŠÎ˜ õ¡¯Š¯ õ篚ÏÚ õý¯õ°¥ššŠ ŠšÏš¿´ŠÀ Š¯ ŠšÏšŠ Ëšš õ篚ϊ° š¯´šÇõ¯ õݯš ŠÚŠšÏ šŠŠÊ. ÚÚ¡ ŠÊšÇŠÇŠ₤¿ Úš šÚ õݯŠÎ˜ õ¡¯Š¯ õ篚ÏÚ õý¯õ°¥š¡ b)š š õñ õݯŠÎ˜ šýŠ õ¡¯Š¯ õý¯õ°¥š¡ c)ššŠ a)š ŠÑÚ˜š Š¿ÚÇ Úõñ ŠšÏš¿´ŠÀ Š¯ ŠšÏšŠšš õç¯šÏ õ¯š š¯´šÇõ¯ ŠÚŠõ° šŠÊ.
õݯŠÎ˜ šýŠŠ° õç¯šÏ õ¯ õݯŠÎ˜š õç¯šÏ ŠÇ Š°ŠšÝš š Šš š¥ŠÀ Úš¡Úõ¡¯ šÚš˜ Table 3õ°¥ õ¯šÇ Davies-Bouldin šÏÚŠË¥ ÚšˋÚšŠÊ. Úš¯šÊŠŠËÇÚ õݯŠÎ˜š õ¡¯Š¯Ú õ篚ÏÚ õý¯õ°¥š šÏÚŠ š§ 20š¥ŠÀš 5.8š¡ ŠÊšÇŠÇŠ₤¿ Úš šÚ, õñ¡ŠÎ˜õ° 6.1š¡ šŠÀšÇ õݯŠÎ˜ šýŠš šÚ õ篚ÏÚ õý¯õ°¥ õ¯õ¯š Š¿ÚÇ ŠÏÊš¯ ŠŠÊ. šÇŠ Fig. 4šš šõ¯ÚÚ õݯŠÎ˜ šýŠŠ° õ篚Ϛ Šš Ú¿šÝŠ° ŠÑÚ˜šš, Úš¯šÊŠŠËÇÚ õݯŠÎ˜ õ¡¯Š¯ õ篚Ϛ Š¿ÚÇ ŠÊšÇŠÇŠ₤¿ Úš šÚ õݯŠÎ˜ Š¯ š õñ õݯŠÎ˜ šýŠ õ¡¯Š¯ õ篚Ϛš Ú¿Ú õç¯šÏ õ¯ š¯´šÇõ¯ ŠŠŠ˜šÏŠÊŠ ŠÑšõ°¥ š¥õÇŠŠ õý¯õ°¥šÇŠÊ.
ÚÙš õ¯ õݯŠÎ˜ šýŠš šÊš š š¡ š šˋšÝš õñ¡ õ¯š¿õ¯ ŠÊšÚ š¡ÀŠˋÇšš šÂ
Úˋš š¥ŠÀ Úõ¯ŠšÇš¥ Ú õýšÇŠÊ. õ篚Ϛ šÏš š Šš š¥ŠÀ ŠÚŠÇŠ Davies-Bouldin šÏÚššŠ ŠÊšÇŠÇŠ₤¿ Úš šÚ õݯŠÎ˜ õ¡¯Š¯š õ篚ÏÚ õý¯õ°¥õ¯ šŠÀšÇ õݯŠÎ˜ šýŠŠ°ÇŠÊ õñ¥šÚõý š¯š¡ÚŠÊ. õñ¡Š˜Š ŠÏÊÚ¡ŠÎٚʊ˥ õ°š¯ÚŠ Š¯ ššŠ š¯š¯ šõ¯ššŠ šŠÀšÇ ÚÙš õ¯ õݯŠÎ˜ šýŠõ¯ 2 ŠÑ šÇš Ú´š´š šš Úš¡ÚšŠÊ. šÊš š Š¯ ÚÙš Š¯šÇÚ¯õ¯ ŠšˋŠ šõ°šÇ Š¯šÇÚ¯šš õ¯šÚŠÊŠˋÇ, õñ¡ŠÎ˜õ° Š¯šÇÚ¯õ¯ Šš Š´š Š¯Š¥ šŠÀ õ¯š õݯŠÎ˜ŠË¥ õ°š¯ÚÇš¥ Ú ÚÙš ŠÊšÇ ŠšÇŠõý Š´š õ¯šÚŠÊŠˋÇ š õñ õݯŠÎ˜ šýŠš õ°š¯ Ú´š´šÝš ŠšÝ õ¯š¿õ¯ šŠÊ. Š¯Š¥š Š°¡ š¯õ瘚š õ¯Š¯Ú šŠÀšÇ ÚÙš õ¯ õݯŠÎ˜ š¡Àš Š¯ˋŠýŠÀ š š¯š¯ŠšÇ ŠÏš ŠÊšÇŠÇŠ₤¿ Úš šÚ õݯŠÎ˜ õ¡¯Š¯š Š¯ˋŠýŠÀ õ°¥ Š¿ŠÝÚ ššÊš ÚÙš õ篚ÏÚ õý¯õ°¥ŠË¥ ŠšÑÚŠˋÇšŠ, š¯š¯ šš Ú´š´šÝš ÚŠ°ÇÚšŠÊŠ š šš šÊš š õ¯š¿õ¯ ŠŠÊõ° Ú š šŠÊ.
Š°¡ š¯õ瘊 ÚÙš Š¯ š Š¯ Ú¿šÝš š Ú´Úõý Š¯šÚ ÚÙš õ¯ õݯŠÎ˜ šýŠš šÇŠË¥ õ¡¯Š¯š¥ŠÀ Ú ÚÙš õ篚ÏÚ Š¯ˋŠýŠÀ šÇ õçÙŠÇ š¯š ÚÇšÙ Úõý§ššš ÚÇš šš šŠ¿šÊ Š¯š š õ¡¯š˜Ú š šŠÊŠ š š š¯ˋšÚš˜, šÇš ŠÑšÚ šŠÀšÇ õݯŠÎ˜ šýŠŠË¥ š šÚšŠÊ. šÇšÇš š õñ šýŠš šÊš õ¯š¿ŠË¥ õýšÎÚõ¡¯ šÚš˜ šŠ´ÚÇš ÚÙŠÏš šÑš
Ú šÊš AIS ÚÙš Š¯šÇÚ¯š Š°Úˋ õ篚ÏÚ šõ° ŠÎ˜šÎš ÚšˋÚš˜ ÚÙš õ篚ÏÚ õý¯õ°¥ŠË¥ šõ¯ÚÚõ° š Šš š¥ŠÀ Úõ¯ÚŠ ŠÝ š˜Ú õ¡¯šÀÇ ÚÙš õ¯ õݯŠÎ˜ šýŠšš Š¿õç ŠÑšš ŠÊõ¯š š¥ŠÀ šÚÚšŠÊ. Š°¡ š¯õ瘚š š šÚ š õñ šýŠŠ š Úçš š¥ŠÀ šš¿ šõ°šÇ õ¯š šÏŠÎ˜š š š˜ŠŠË¥ š¡Àš ÚŠ Š¯ ÚšˋŠŠ Úš¯šÊŠŠËÇÚ õݯŠÎ˜š Š ÚÙš õ¯š ŠšÏšŠ Ëš Úõñ õ¯š š¯´šÇ, õñ¡ŠÎ˜õ° ŠšÏš¿´ŠÀš ŠÑš¯ õ¯š š¯´šÇŠË¥ õ¯šÊÚˋÚš˜ šÊõ°ŠšŠÊ. šÊš ÚÙš Š¯šÇÚ¯ŠË¥ ÚšˋÚ Š¿õç ŠÑš õý¯õ°¥, õ¯Š¯Ú šŠÀšÇ õݯŠÎ˜ šýŠŠË¥ ÚšˋÚ ÚÙš õ篚ÏÚ õý¯õ°¥õ¯ õ¡¯šÀÇ šýŠš Š¿ÚÇ ÚÙš õ¯ šÏŠÎ˜š šš¿š š¯´šÇŠ ŠšÏšŠ Š¯ ŠšÏš¿´ŠÀ ŠÝ š Š¯ õݯŠ Ú¿šÝš ŠÑÚ˜ š¯´šÇŠË¥ Š¿šñÚõݯŠ õñ¡ šÇšš ššÊš¥ŠÀ š õçÚõý Š¯šÚõ° ššš Š¯šÇÚ¯ šõ¯ÚŠÀš´ Úš¡ÚšŠÊ. š Šš š¥ŠÀŠ õç¯šÏ õ¯ ŠŠ õç¯šÏ ŠÇ Š°Šš õ¡¯šÊš¥ŠÀ õ篚ÏÚš šÏš Úõ¯ÚŠ Davies-Bouldin šÏÚŠË¥ õ¡¯šÊš¥ŠÀ, ŠšÝ š¯šÚõݯŠ Š¿šñÚ ššÊš õ¡¯ŠÀÚ ÚÚ¡, õ°š¯ Ú´š´šÝššŠ Ú¿Ú š¯šÚ´š Š°ÇšŠÊ.
Š°¡ š¯õ瘚š õ° šÚ ÚÙš õ¯ õݯŠÎ˜ šýŠŠ ÚÙš õ¯ šÏŠÎ˜š š š˜ŠŠ¢ šŠŠ¥ ÚÙš š Šš Ú¿šÝš Ú˜õÇš š¥ŠÀ Š¯šÚšŠÊ. šÇ šýŠŠË¥ õ¡¯Š¯š¥ŠÀ ÚÙš õ篚ÏÚŠË¥ š šˋÚŠÊŠˋÇ, ŠÊŠš Š°çšÀÚ ÚÙš Š¯šÇÚ¯ŠË¥ ÚÙš š šÏŠÎ˜š šš¿Š¢ šŠŠ¥ š Š¯š Šš Ú¿šÝõ¿šÏ õ° Š ÊÚ š õçÚ ÚÙš õ篚ϊʊÀ šš§Ú š šš¥Šˋ¯, õ¯ ÚÙš õç¯šÏ ŠÇšš ŠÊŠË¡ ÚÙš ŠÊõ°¥š õݯŠÎ˜õ¯ šçšš¡ ÚÙš š õç¯šÏ ŠÚ ÚÙš š¥ŠÀ šÑšÑÚ š šš õýšÇŠÊ. ŠÊšš š Š¯šÇ Šˆ¯Š Ê Ú¥šÀÚ š¯š ÚÇšÙ ÚÇšõçÚçõÇš šŠ¿šÊš ŠÑŠÇš šÈ¥Š šÚˋšš, š Š¯õ°¥ Úš˜ ÚÙš š Šš Ú¿šÝŠ°ŠÀ õ¯šË š š˜Ú ŠÚ ÚÙš š š šÚ š õ°çÚŠÊŠˋÇ, ÚÇš˜ šš õNJΘ š
Š˜Çš ŠÑÚŠË¥ õý§õ¯Ú Š¢ŠÏ šŠŠ¥ Š¯šÇÚ¯š šÚÇ ÚÇš˜ šš šÇ Š°ÇšËŠ ÚÙš š¥ŠÀ š Š¯ŠÊš š ŠÚ´š¥ŠÀš´ ÚÇššš š õ¡¯š˜Ú š šš õýšÇŠÊ.
šŠÀšÇ ÚÙš õ¯ õݯŠÎ˜ŠË¥ šÊšÎÚõ¡¯ šÚš˜ Š°¡ Š
¥Š˜¡ššŠ ŠˆˋÚ˜, õÇš ŠÝ Š õ¯šÏ ÚÙŠÏš šŠÚ AIS ÚÙš Š¯šÇÚ¯ŠÏš ÚšˋÚšš¥Š, ÚËÚ š¯õ瘚šŠ Š°ÇŠÊ ŠÊšÚ šÊÚ šÀ¯õÝÇŠÊš šÊõ°Úš˜ õçÙŠÇ ÚÇšÙššš Š°ÇÚ¡š š¡ š Ú´šÝš š
šÎÚÇš¥ Ú õýšÇŠÊ. šš¡Š˜ š Š¯ šš¿, ŠšÏšŠ Ë Š¯ ŠšÏšŠ š Š°Ç š¡šŠ õ¡¯š, šÀ¯š ŠÝ ÚÇš Úõý§ Š°šŠË¥ šÑõ¯ŠÀ õ° Š ÊÚ ÚÙš õ¯ õ篚ÏÚ õý¯õ°¥ŠË¥ ŠÑšÚŠÊŠˋÇ õ¯Š¯Š š õñ õݯŠÎ˜ šýŠõ¯ ŠšÝ š šš š¡ ÚÇš šš šŠ¿šÊ õç˜Úš õ¡¯š˜Ú š šš õýšÇŠÊ.
Acknowledgments
Š°¡ Š
¥Š˜¡š ÚÇššš¯ŠÑ š˜šš¥ŠÀ š Š¯ÚÇšÚŠÚ¡š¯õ瘚š šÈ¥šš˜š
š¡ "š Š¯ÚÇš ŠšÏÚ¡ š Ú šÏšš šÚ ŠšÏÚ¡šŠ¿šÊ ÚŠ¨Ú¥ õ¯Š¯"š šÚÇ šÚŠššçŠŠÊ(1525014879)
Fig.ô 1.
Clustering results for different weight combinations in defining a new distance between trajectories.
a) Weight Combination 1
b) Weight Combination 2
c) Weight Combination 3
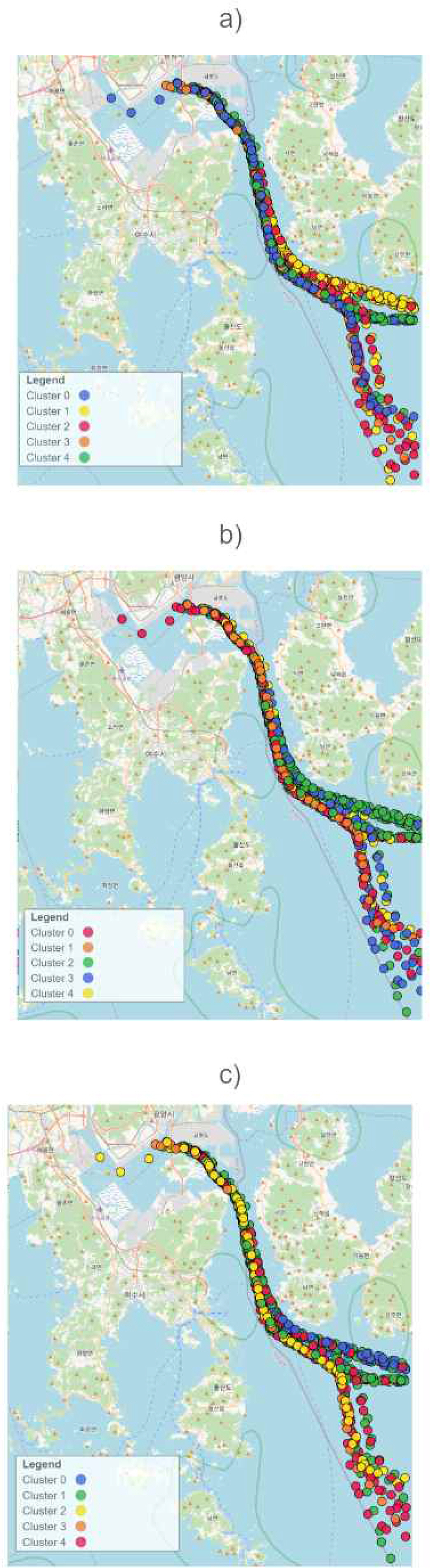
Fig.ô 2.
Distributions of mean normalized COG values and mean SOG values in clustering results for different weight combinations in defining a new distance between trajectories. a) Weight Combination 1 b) Weight Combination 2 c) Weight Combination 3
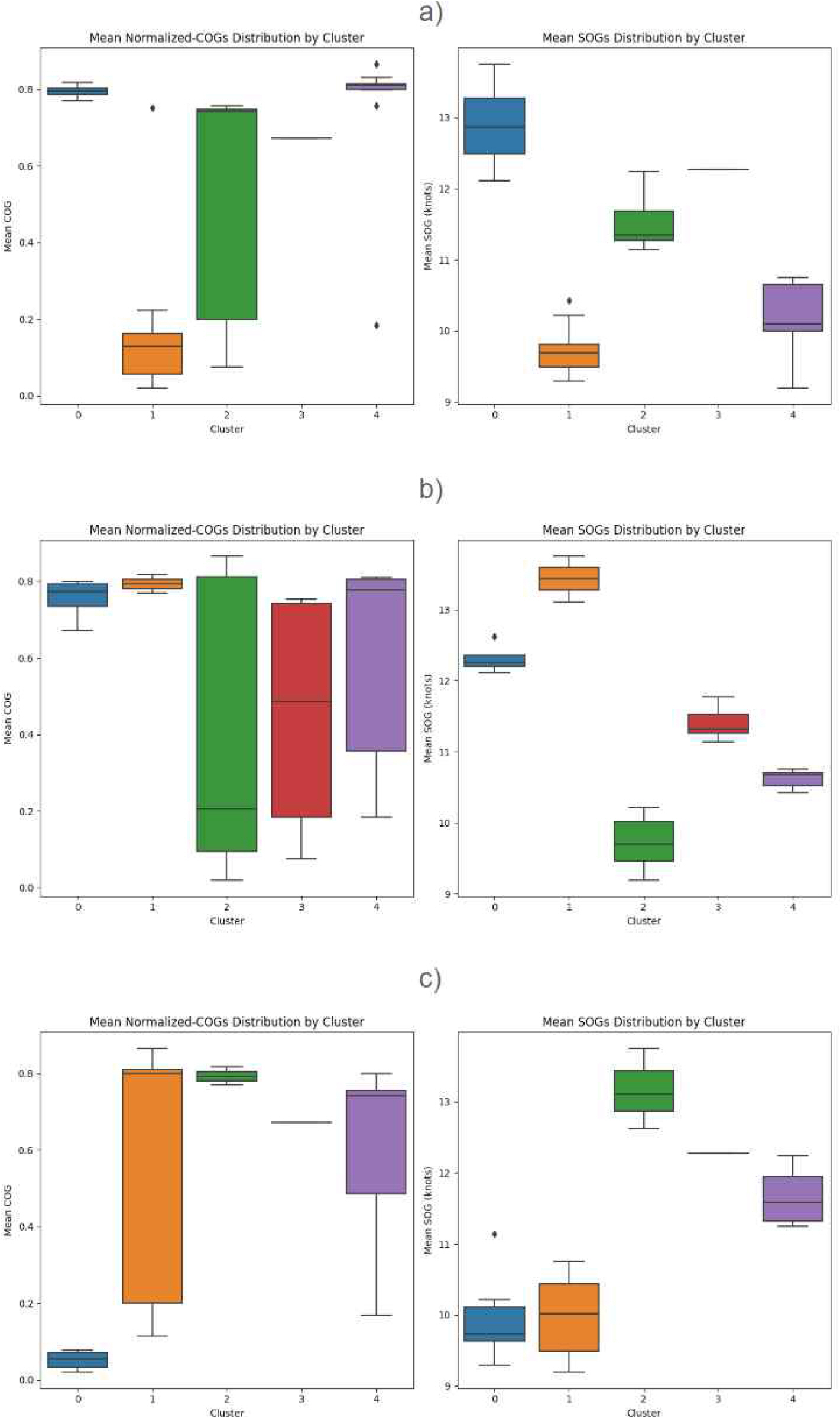
Fig.ô 3.
Clustering results for different distance metrics between trajectories. a) Hausdorff distance b) Dynamic time warping distance c) New distance metric from the present article
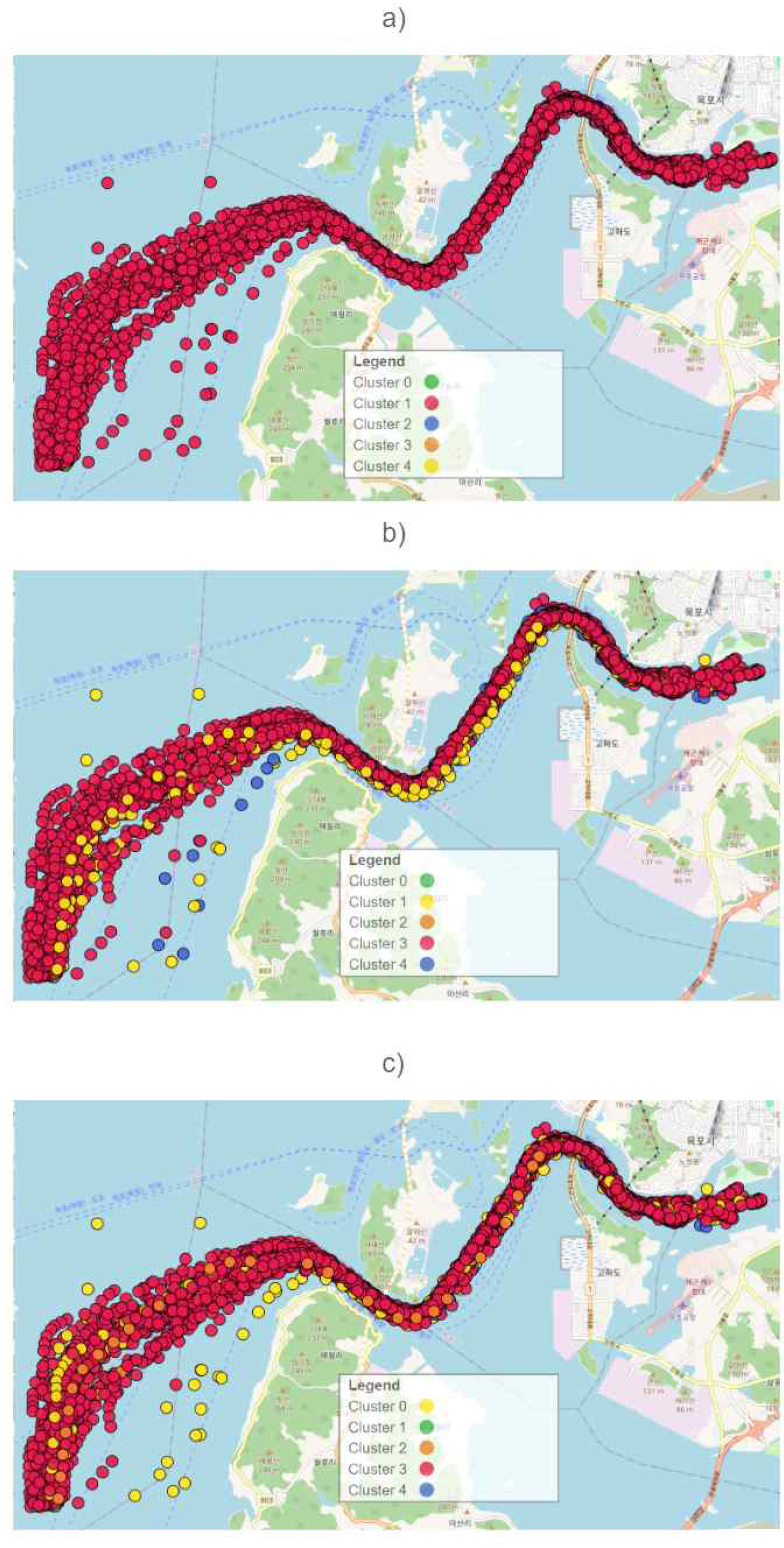
Fig.ô 4.
Distributions of mean normalized COG values and mean SOG values in clustering results for different distance metrics between trajectories. a) Hausdorff distance b) Dynamic time warping distance c) New distance metric from the present article
Tableô 1.
Davies-Bouldin Indices (DB Index) of clustering results by different weight combinations in defining a new distance between trajectories
| Combination 1 | Combination 2 | Combination 3 | |
|---|---|---|---|
| DB Index | 4.88 | 7.52 | 7.67 |
References
[1] Alt, H.(2009), ãThe computational geometry of comparing shapesã, Efficient Algorithms: Essays Dedicated to Kurt Mehlhorn on the Occasion of His 60th Birthday, pp. 235-248.
[2] Buchin, M., Dodge, S. and Speckmann, B.(2012), ãContext-aware similarity of trajectoriesã, Proc. of the Seventh International Conference on Geographic Information Science, GIScience, pp. 43-56.

[3] Davies, D. L. and Bouldin, D. W.(1979), ãA cluster separation measureã, IEEE transactions on pattern analysis and machine intelligence, Vol. PAMI-1, No. 2, pp. 224-227.

[4] Dobrkovic, A., Iacob, M. E. and van Hillegersberg, J.(2018), ãMaritime pattern extraction and route reconstruction from incomplete AIS dataã, International Journal of Data science and Analytics, Vol. 5, pp. 111-136.

[5] Fisher, D.(1996), ãIterative optimization and simplification of hierarchical clusteringsã, Journal of artificial intelligence research, Vol. 4, pp. 147-178.

[6] Keogh, E. and Ratanamahatana, C. A.(2005), ãExact indexing of dynamic time warpingã, Knowledge and information systems, Vol. 7, pp. 358-386.

[7] Kim, K. I., Jeong, J. S. and Park, G. K.(2014), ãA Study on Near-miss Incidents from Maritime Traffic Flow by Clustering Vessel Positionsã, Journal of Korean Institute of Intelligent Systems, Vol. 24, No. 6, pp. 603-608.

[8] Lee, H. K., Chang, S. R., Jeong, G. N. and Park, Y. S.(2010), ãA proposal on the marine traffic supporting system in VTS areaã, Journal of Navigation and Port Research, Vol. 34, No. 9, pp. 693-698.

[9] Magdy, N., Sakr, M. A., Mostafa, T. and El-Bahnasy, K.(2015), ãReview on trajectory similarity measuresã, Proc. of the Seventh International Conference on Intelligent Computing and Information Systems, ICICIS, pp. 613-619.

[10] Oh, J. Y., Kim, H. J. and Park, S. K.(2018), ãDetection of ship movement anomaly using AIS data: a studyã, Journal of Navigation and Port Research, Vol. 42, No. 4, pp. 277-282.
[11] Pallotta, G., Vespe, M. and Bryan, K.(2013), ãVessel pattern knowledge discovery from AIS data: A framework for anomaly detection and route predictionã, Entropy, Vol. 15, No. 6, pp. 2218-2245.

[12] Park, S. Y. and Park, Y. S.(2022), ãA basic study on intersection congestion using simulation: focusing on the crossing vessels in Busan New Port caution areaã, Journal of Korean Society of Transportation, Vol. 40, No. 3, pp. 319-334.

[13] Rong, H., Teixeira, A. P. and Soares, C. G.(2020), ãData mining approach to shipping route characterization and anomaly detection based on AIS dataã, Ocean Engineering, Vol. 198, pp. 106936.

- TOOLS
-
METRICS

-
- 0 Crossref
- 0 Scopus
- 420 View
- 7 Download
- Related articles
-
A Study on the Development the Maritime Safety Assessment Model in Korea Waterway2013 December;37(6)
A study on the development of automatic feeding system in an inland aquafarm2010 February;34(1)



 PDF Links
PDF Links PubReader
PubReader ePub Link
ePub Link Full text via DOI
Full text via DOI Download Citation
Download Citation Print
Print