|
 |
| J Navig Port Res > Volume 47(2); 2023 > Article |
|
ABSTRACT
Ships need to ensure safety during their navigation, which makes route determination highly important. It must be accompanied by a route following controller that can accurately follow the route. This study proposes a method for automatically generating the ship route based on deep reinforcement learning algorithm and following it using a route following controller. To generate a ship route, under keel clearance was applied to secure the ship's safety and navigation chart information was used to apply ship navigation related regulations. For the experiment, a target ship with a draft of 8.23 m was designated. The target route in this study was to depart from Busan port and arrive at the pilot boarding place of the Ulsan port. As a route following controller, a velocity type fuzzy PID controller that could compensate for the limitation of a linear controller was applied. As a result of using the deep Q network, a route with a total distance of 62.22 km and 81 waypoints was generated. To simplify the route, the Douglas-Peucker algorithm was introduced to reduce the total distance to 55.67 m and the number of way points to 3. After that, an experiment was conducted to follow the path generated by the target ship. Experiment results revealed that the velocity type fuzzy PID controller had less overshoot and fast settling time. In addition, it had the advantage of reducing the energy loss of the ship because the change in rudder angle was smooth. This study can be used as a basic study of route automatic generation. It suggests a method of combining ship route generation with the route following control.
Generally, a ship's route is planned during the voyage in such a way that it ensures the stability of the ship against sinking and stranding while minimizing voyage time and fuel consumption (Ozturk et al, 2022; Orsic et al, 2016; Roh, 2013). Previously, navigators with specialized knowledge determined the route by hand; however the development of autonomous navigation technology (Kim et al, 2019), automation of route generation has become necessary.
Although most of studies from a route planning perspective have been limited to experimenting with short distances, this study focuses on port-to-port. Herein, under keel clearance (UKC) and navigation chart information were applied to ensure ship safety and compliance with navigation regulations, and reinforcement learning-based deep Q-Network (DQN) algorithm was applied to generate the route. Existing studies related to route planning use various path planning algorithms such as the Dijkstra algorithm, and the A* algorithm which are traditional path planning algorithms. Novac et al. (2020) proposed a study that can automatically generate a ship route using the Dijkstra algorithm, but targeted a short route that did not consider various factors such as water depth and navigation rules that are considered when planning an actual route. In the study of Lee et al. (2022a), based on the automatic identification system data, the Dijkstra algorithm and the A* algorithm were used to automatically generate the vessel's passage plan. However, these traditional algorithms have disadvantages in that these algorithms can provide limited possibilities for complex cases, have low path smoothness, excessive orthogonal rotation, and reduce the effectiveness of the algorithm as the map scale expands. Unlike the Dijkstra, A* algorithm, which simply finds the shortest distance (Lie et al, 2019; Wang et al, 2019), DQN has the advantage of generating routes, satisfying sea conditions and navigation regulations through rewards. With these advantages, reinforcement learning-based DQN is being studied as one of the powerful methods for generating ship routes. Chen et al. (2019) proposed a ship path generation method based on Q-learning to achieve autonomous navigation of ships without relying on experience. And, Guo et al. (2021) compared the BUG2 algorithm, the artificial potential field algorithm, the A* algorithm, and the DQN algorithm, and DQN was derived as the algorithm with the best performance for generating ship routes. Therefore, this study adopted DQN as an algorithm for route generation.
Meanwhile, the ship's optimal route must be accurately followed after it has been determined. To follow a route accurately, an autopilot controller is attached to the ship to control the ship (Roland, 1992). The autopilot controller should have accurate and fast capabilities of alter course and should not produce an overshoot for large changes in heading angle. It should also be able to prevent rough changes in steering angle to reduce unnecessary energy losses. A widely applied autopilot controller in the past has been the linear Proportional-Derivative (PD) controller, which has a simple structure and is easy to design(Kim et al, 2009). Despite these advantages, linear PD controllers can only be applied to single input-output systems, and it is difficult to obtain satisfactory performance when applied to systems with strong nonlinearity.
Recently, with the development of modern control theory, studies that apply linear controllers into multi-variable systems or nonlinear systems. Also studies that apply fuzzy theory are being conducted(Nam et al, 1994; Kim et al., 2021). Fuzzy controllers can incorporate expert linguistic information into the controller and become excellent nonlinear controllers due to their nonlinear characteristics (He et al, 1993).
Therefore, in this study, we propose a velocity-type fuzzy (Proportional-Integral-Derivative) PID controller that can overcome the shortcomings of the linear PD controller and provide various functions that are essential to an autopilot controller. The proposed velocity-type fuzzy PID controller consists of a fuzzifier, a control rule, and a defuzzifier. Moreover, it has the same control structure as the linear PD controller but the gain of the controller is not fixed. Besides, a velocity-type fuzzy PID controller has an improved self-tuning ability compared to that of a liner PD controller. The ability to self-tuning allows for the precise and fast alter course that are essential to an autopilot controller and allows the ship to be controlled to turn without considerable overshoot for large changes in heading angle. To verify the performance of the proposed autopilot controller, simulations are conducted using the route generated by DQN and ship models. This study can be proposed as a basic study of route automatic generation, and suggests a method of combining with the route following control.
Generally, a ship's equation of motion can be expressed as 6 degree of freedom (DOF) equation of motion(Lee et al, 2004; Kim et al., 2023), and comprises the sum of rigid body and hydrodynamic equations. The ship's 6 DOF equation of motion is shown in Equation (1).
It consists of a vector ╬Į = [u, v, w, p, q, r]T, where (u, v, w) are the linear velocities in three axes about the ship's body fixed coordinate system, and (p, q, r) are the angular velocities in three axes. The inertia matrix M is represented by MRB +MA as the sum of the rigid body and hydrodynamic inertia matrices, and Coriolis and centripetal force matrixC (╬Į) is represented by CRB (╬Į) +CA (╬Į) as the sum of the rigid body and hydrodynamic Coriolis and centripetal force matrices. The damping matrix D(╬Į) is D +Dn(╬Į), which is the sum of the linear damping matrix and the nonlinear damping matrix. g(╬Ę) is the term associated with the restoring force, and Žä is the force and moment term, which includes the thrust and rudder to control the ship.
Meanwhile, since most ships travel at sea level, the ship can be assumed to have a 3 DOF equation of motion with translational motion about the x, y axes and rotational motion about z axis. To derive the 3 DOF equation of motion, the following conditions must be satisfied.
Under these conditions, the ship's 3 DOF equation of motion can be expressed as a combination of a forward speed model and steering model.
Here, m and u are the mass and forward speed of the ship, respectively, and Xu╠ć and X|u|uare the added mass and drag coefficient for the surge direction of the ship, respectively. t and T represent the propeller reduction factor and propeller thrust. And the steering model of the ship is represented by Equation (3)(Davidson, 1946).
Here, it is defined as a vector ╬Į = [v, r]T, ╬┤ is the ship's rudder angle as a control input. The inertia matrix Mm, the sum of the Coriolis and centripetal force matrix and damping matrix N (u)m, and the input matrix bm can be expressed as Equation (4)
Here, xG is the x axis coordinate of the ship's center of gravity and Iz is the moment of inertia about z axis. Yv╠ć, Yr╠ć, Yv, Y╬┤, Nr╠ć, Nr, N╬┤ are the hydrodynamic coefficients for sway, yaw. From the above equations, the ship's 3 DOF equation of motion is derived.
In order to analyze a moving ship based on the ship's body fixed coordinate system, the body fixed coordinate system must be converted to the earth fixed coordinate system. To convert the earth fixed coordinate system, it can be obtained by taking a transform matrix for the ship's speed and angular, and the transform matrix is as shown in Equation (5).
Here, x, y and Žł are the positions of the ships along the x,y axes and Žł is the ship's heading angle.
The specifications of the target ship of this study are shown in Table 1.
Here, L is the ship length, Lpp is length between perpendiculars, T is draft, B is maximum beam and Ōłć is displacement.
In this study, a velocity-type fuzzy PID controller was used as a route following controller. The structure of the velocity-type fuzzy PID controllers shown in Fig. 1 (Kim et al, 2000).
Generally, a velocity-type fuzzy PID controller is a controller that takes an error signal and the rate of change of the error as inputs and applies fuzzy rules and inference in real time to determine the control incremental.
Fig. 1 is the structure of the velocity-type fuzzy PID controller, as proposed in this study. The velocity-type fuzzy PID controller is a controller that uses the heading angle error Žłe(k) at the current sampling time k, the velocity Žłr (k) of Žłe(k), and the acceleration Žła(k) of Žłe (k) as inputs, and determines the control output through fuzzy rules and inference in real time. The control output is the control increment d╬┤c(k) of the rudder that controls the actual ships. At this point, d╬┤c(k) is added to the rudder angle ╬┤c(k ŌłÆ 1) generated at the previous sampling time, resulting in the final rudder angle ╬┤c(k) are generated as the ship's control input. GE (k), GA (k) and GR (k) are the input scale parameters for normalizing the three inputs and GU (k) is the scale parameter for the fuzzy output.
Fig. 2(a) shows the membership function of a fuzzy set defined in the scaled input variable space.
Žł e * Žł r * Žł r *
The fuzzy control rules are generated based on the professional knowledge and experience of the expert and are shown in Table 2 (used in this study).
In the control rules (R1)1 Ōł╝ (R4)1, for fuzzy control block 1 and in the control rules (R1)2 Ōł╝ (R4)2, for fuzzy control block 2, Zahdeh's AND logic is applied, which performs a MIN operation to find the fitness of the latter for two conditions of the former.
The defuzzification algorithm used in this study is the center of gravity method(Kwak et al, 2018), and the outputs d╬┤1(k) and d╬┤2(k) of the fuzzy control blocks 1 and 2 through defuzzification are summed. Furthermore, the output scale parameter GU(k) is multiplied to finally generate the control increment d╬┤c(k). Organizing d╬┤c(k) according to the fuzzy control rules can result in the formation of a very simple PID, as shown in Equation (6).
Here, the integral, proportional and derivative coefficients Ki(k), Kp(k) and Kd(k) are as shown in Equation (7).
In this study, DQN algorithm based on reinforcement learning was applied to generate the ship's route. Reinforcement learning is a method in which an agent learns to maximize its reward through interaction with its environment. Since we are aiming to generate a route for a ship, the ship will be the agent, and the environment will need the information important for generating the route.
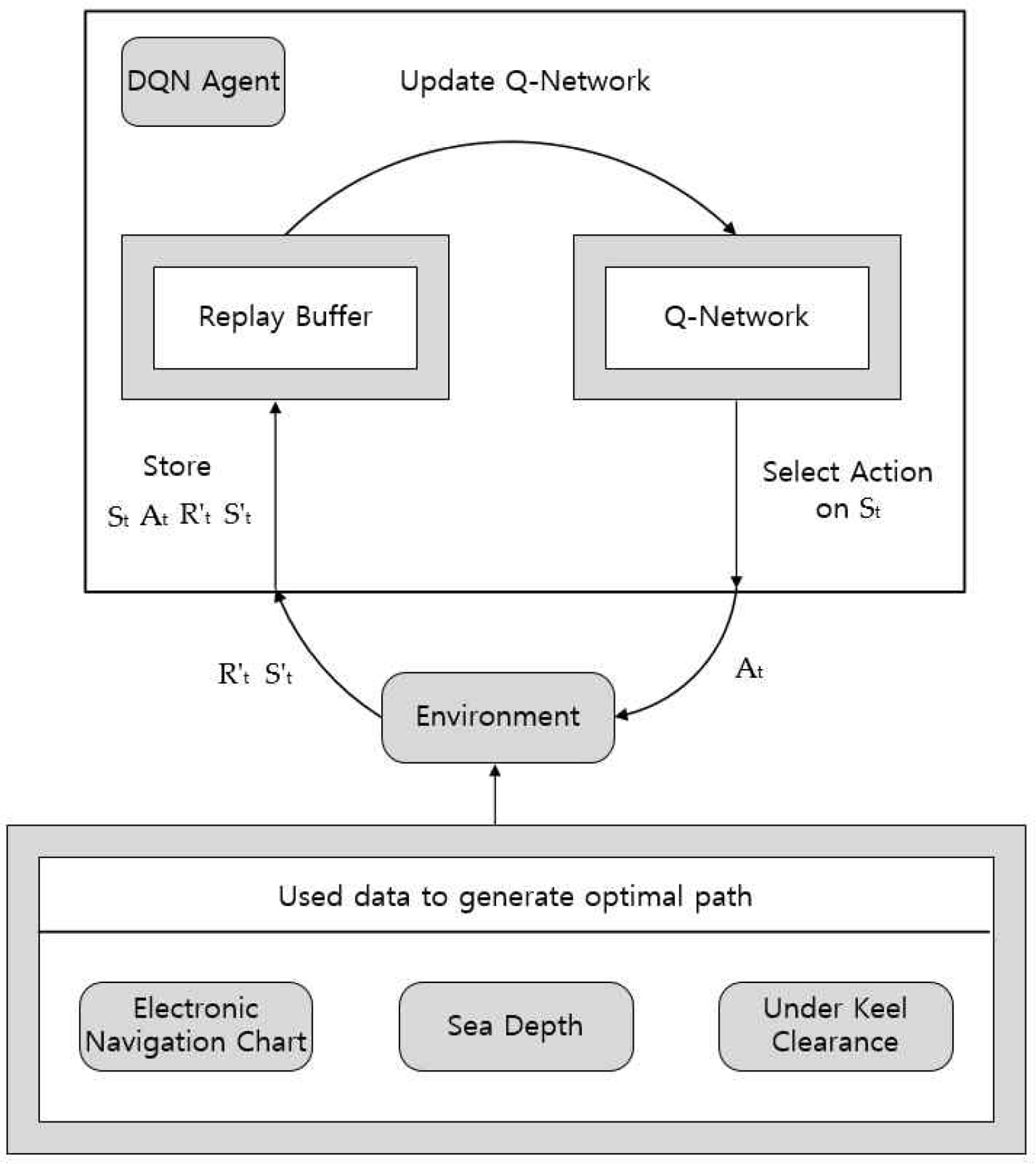
Fig. 3 shows the structure of the environment and the DQN algorithm to generate the ship's route.
Since this study aims to generate routes for ships, it is important to create an environment enabling the ships to find their route. Hence depth information, UKC and sea state information are incorporated into the environment to ensure the safety of ships and apply regulations for navigation.
DQN is an evolution of Q-learning that adds a neural network and replay buffer to Q-learning (Logan et al, 2021). Q-learning has the disadvantage that it is difficult to apply in a complex environment because Q-function is found using the Q-table corresponding to each state when the number of states is very large. And the correlation between the current state and the next state is very high, so agent tends to learn only as agent learned. However, since DQN has the advantage of being able to be applied in complex environments as it uses a Q-network to approximate the Q-table, it can reduce correlation because it stores and uses past information through a replay buffer.
As shown in Fig. 3, the DQN will take the optimal action At in the current state St through the optimal policy determined by the Q-network, and the agent will receive the next state StŌĆ▓ and reward RtŌĆ▓ in the environment. At this time, past information St, At, RtŌĆ▓, StŌĆ▓ is stored in the replay buffer, and Q-network is continuously updated based on the stored information. The neural network in DQN is oriented towards minimizing the loss function, which is given by Equation (8).
Here, L (╬Ė) is the loss function, ╬Ė is the parameters of the Q-network, and ╬ĖŌłÆ is the a parameters of the target network. Target network is a neural network with the same parameter values as the Q-network. The Q-network does not learn with a clear goal because the neural network is constantly updated during the coursed of finding the optimal behavior. To solve this problem, we keep the parameter values of the target network fixed and train in the desired target direction and then copy the updated parameters of ╬Ė back to ╬ĖŌłÆ for training.
Meanwhile, the state defined as the coordinates corresponding to current agent's location, and a total of 8 action spaces (Ōåæ, Ōåō, ŌåÉ, ŌåÆ, Ōå¢, ŌåŚ, Ōåś, ŌåÖ) that can act in the current state are defined.
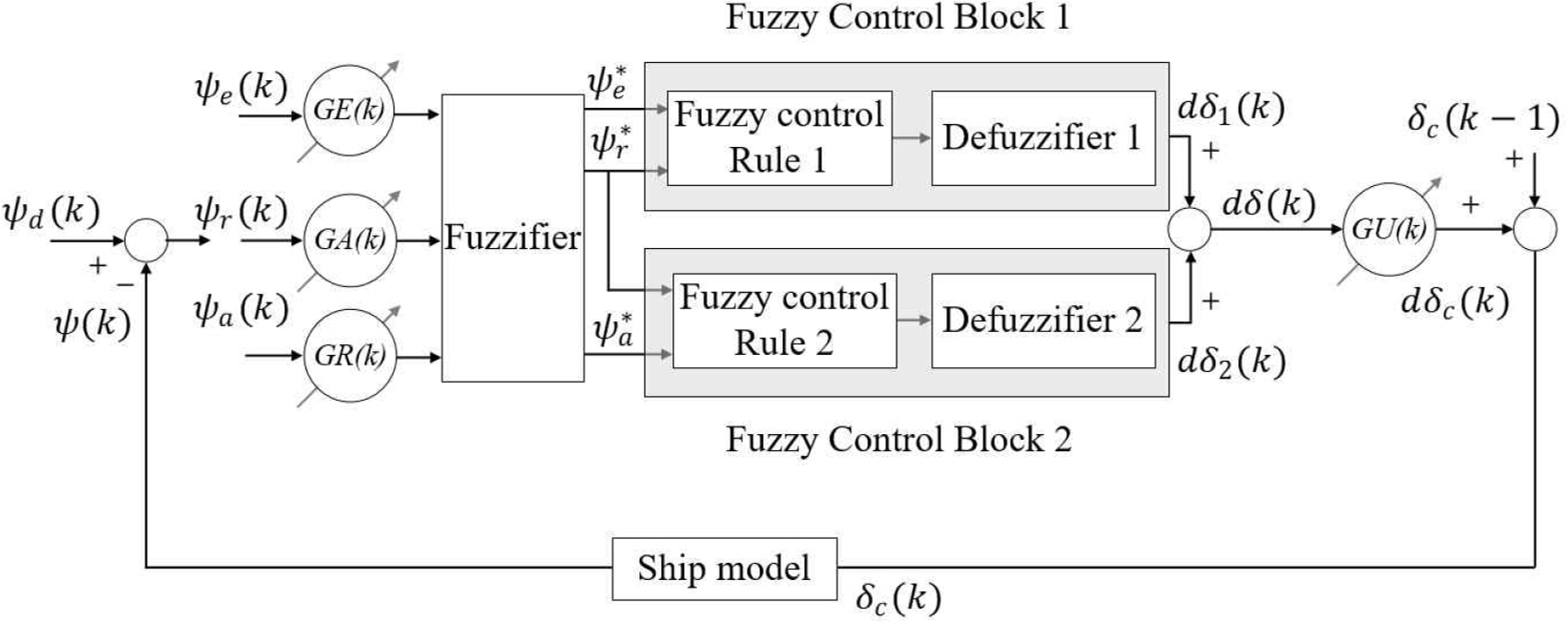
The DQN algorithm essentially generates the route from grid-based pixels. This creates a lot of unnecessary way points and also has the disadvantage of making the route longer (Lee et al., 2022a). To compensate for this, we need to introduce the Douglas-Peucker (DP) algorithm, which simplifies the route and eliminates unnecessary way points. The concept of the DP algorithm is illustrated in Fig. 4 (Zhao et al, 2018).
First, find a straight line connecting the start and end points on the initial route, then find the point with the greatest distance from the straight line. If the distance is greater than the threshold distance (b), keep the farthest point. Repeating the same method for every point on the initial route can simplify the route, as shown in the red line in Fig. 4.
In this study, we aimed to generated a route from Busan port to the pilot boarding place of the Ulsan port. The longitude and latitude values of the target area are (128.90┬░ Ōł╝ 129.79┬░) and (34.60┬░ Ōł╝ 35.59┬░), respectively.
To ensure the safety of the ships, in this study, the UKC was selected to be 11m based on reference(Lee et al, 2019), and GEBCO's bathymetric data was used to reflect the sea depth information. GEBCO's bathymetric data consist of 400m ├Ś 400m per pixel, and if the data is greater than 0m, it is selected as an island or land, and if it is less than 0m, it is selected as a sea. However, by applying the UKC of the ship, the area deeper than 11m was selected as a navigable area, and the area shallower than 11m was selected as an non-navigable area.
Navigation chart information was used to ensure that ships met navigation regulations. The navigations chart information includes traffic separation scheme (TSS), pilot boarding place, and restricted areas (Lee et al., 2022b). TSS is guideline to protect the ship's entry and exit direction for the safety of the ship and reflected restricted areas to ensure that the route does not go too close to land.
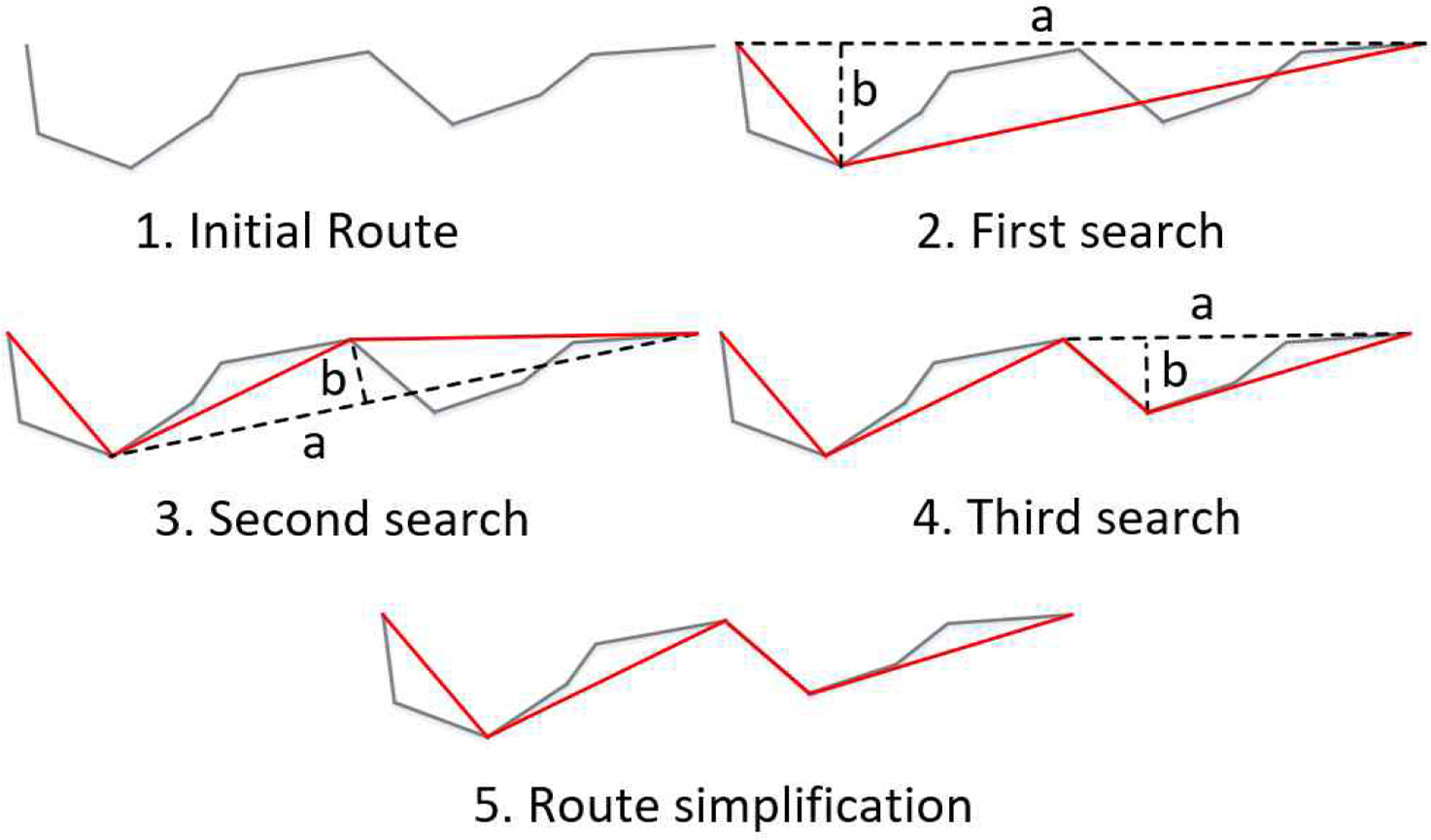
The environment built to generate the ship's route with this information is shown in Fig. 5.
Here, the gray squares are islands and land; the red squares are depth restrictions based on the shipŌĆÖs UKC; and the blue squares are restrictions to prevent the shipŌĆÖs course from getting too close to land. In addition, the orange squares are the passage separation boulevard, through which ships entering Busan Port must pass. Therefore, the above mentioned four circled areas correspond to non-navigable areas that ships should not pass through. However, white squares with water depths greater than 11 meters or green squares represented by TSS(A) are designated as navigable areas for ships to navigate.
The DQN parameter values and reward conditions for generating ship route in this study are shown in Table 3.
Table 3 shows the DQN parameters and reward conditions used in our experiments. To give the agent enough learning experience, we set ŌłŖ-greedy to 0.2, the learning rate to 0.002, and the discount factor to 0.9. The discount factor is a value that determines how much of a future reward will be received at present. Then the replay memory and batch are each set to 2000 and 64, respectively. The activation function of the DQN neural network used RELU.
As the agent explored the area, if it found itself on land or an island, it stopped training immediately to reduce training time, and if it found in non-navigable area, and area where a path should not exist, it was given a penalty of ŌłÆ1. If agent located in the TSS(A) are, which must be passed through when leaving Busan port, 1 was given as a reward, and 10 was given as a reward if agent located at the destination, Ulsan port pilot boarding place.
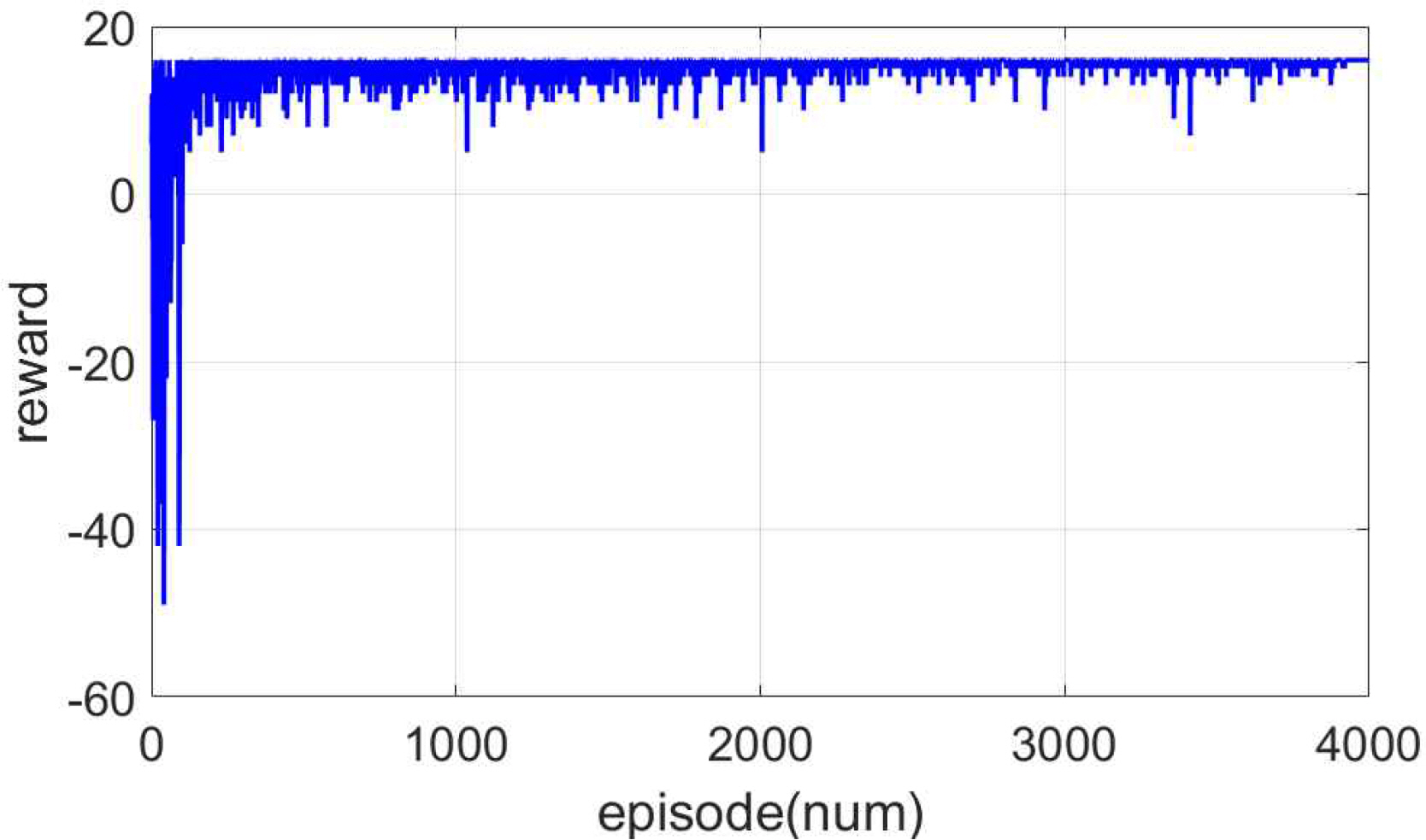
Fig. 6 is a simulation result showing the reward change taken by the agent for each episode. During about 4000 episodes, it can be confirmed that the agent sufficiently experiences penalty and reward. After 4000 episodes, the reward value converged to about 16 and the learning progressed sufficiently. The training time was 52 minutes 45 seconds.
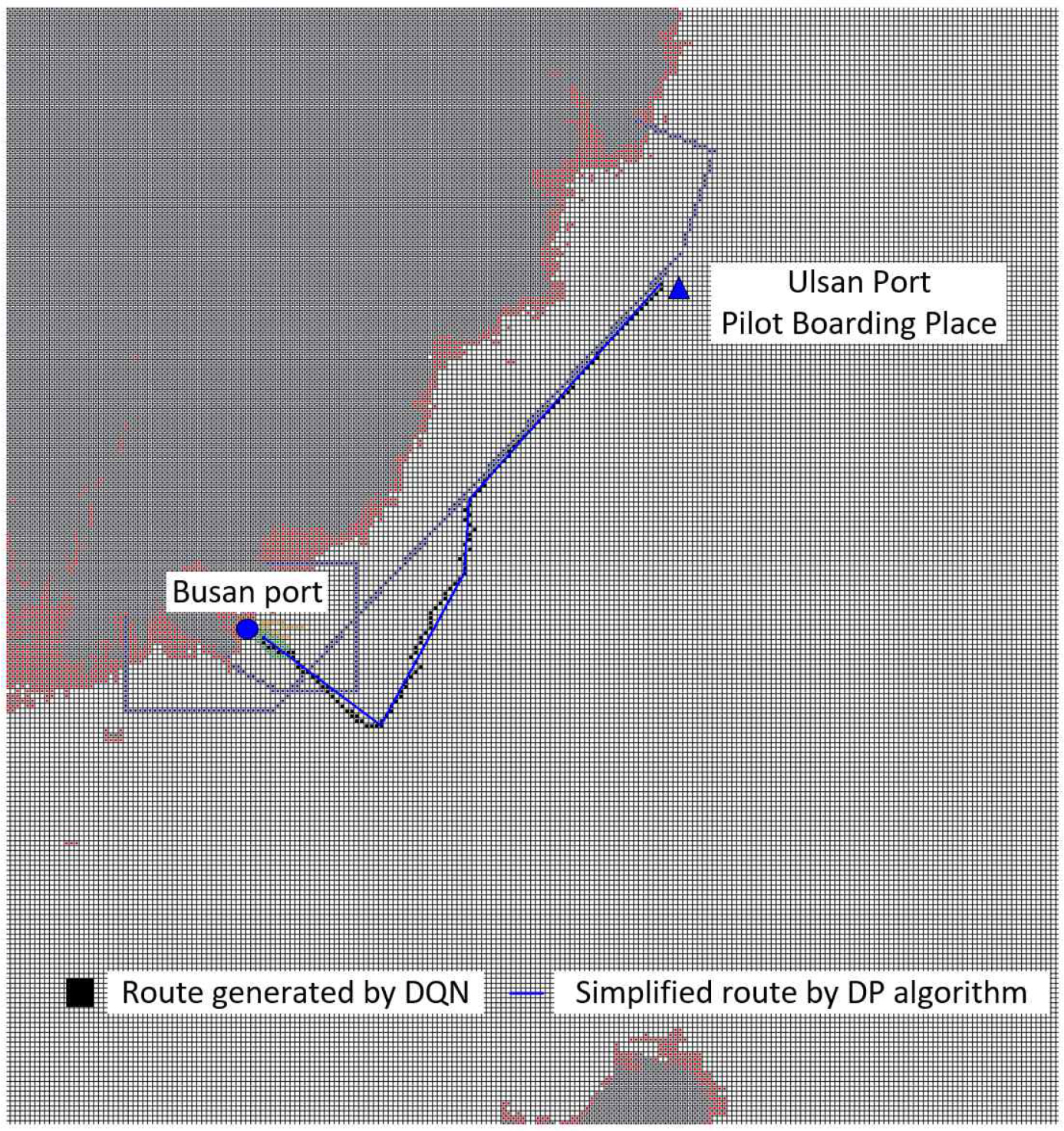
The generated route under these conditions are shown in Fig. 7. The black squares are the route generated by the DQN. As expected, since the route is generated pixel by pixel, a lot of unnecessary way points can be observed, and the route do not exactly follow a straight line. To resolve these issues, we applied the DP algorithm the results are shown in the blue solid line. After applying the DP algorithm, we can see that the number of way points is considerably reduced to three, and the distance of the route is reduced compared to that in the DQN. The route initially generated using DQN had the total distance of 66.22 km and 81 way points, and final route generated by Douglas-Peucker algorithm had total of 55.67 km and 3 way points.
Since reinforcement learning proceeds in a direction that maximizes reward, we can see that the rewarding region, TSS(A), is always traversed and no route are generated in the non-navigable areas.
The performance of the velocity-type fuzzy PID controller proposed in this study is analyzed and compared with that of the widely used PD controller on the route generated in Chapter 4. The proportional and derivative gains of the PD controller were optimized to 1 and 70, respectively. For both controller, the forward velocity of the ship was set to 8m/s, and the maximum angle of the rudder was limited to ┬▒ 20┬░ to secure the stability of the ship.
The longitude and latitude values of the location of the way points are (129.11┬░, 35.06┬░), (129.21┬░, 34.98┬░), (129.28┬░, 35.11┬░), and (129.29┬░, 35.18┬░). The tracking heading angle between way points for route following control are ŌłÆ 137.5┬░, ŌłÆ 24.2┬░, ŌłÆ 3.12┬░, and ŌłÆ 35.92┬░. The reference heading angle used as a control input to follow the route was the angle between the current ship's position and the next way point's position. The reference heading angle can be expressed as in Equation (9).
Here, Žłd(k) is the reference heading angle. xd and yd are the position of the next way points, respectively and x(k) and y(k) are the current ship's position, respectively.
Fig. 8 shows the result of the ship's route following control using a PD and a fuzzy PID controller. We can see that both controller maintain the route accurately in the big picture; however, the PD controller has its limitations when it comes to alter course. The limitations of the PD controller are addressed in Fig. 10 and Fig. 11.
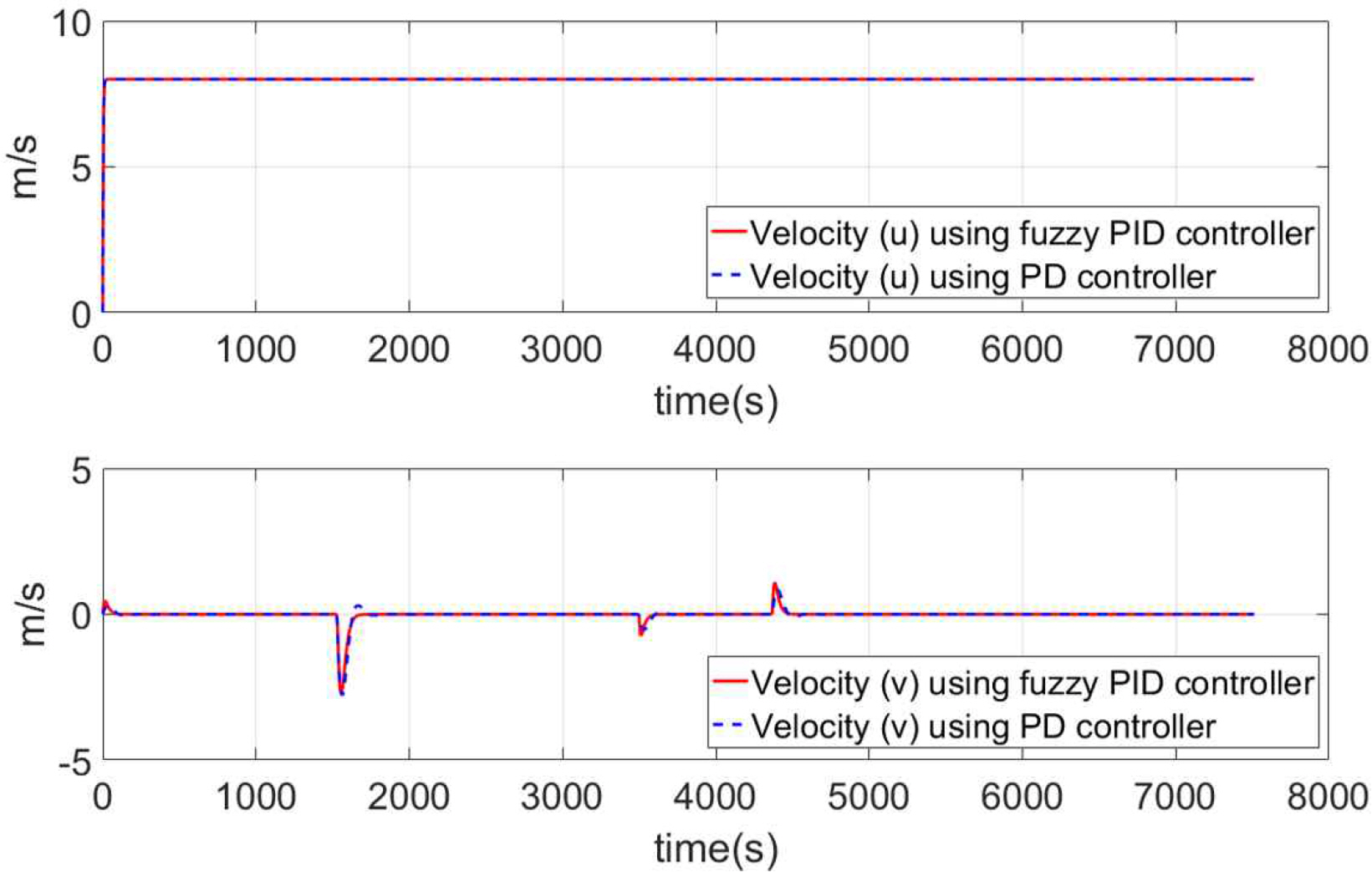
Fig. 9 shows the forward and lateral velocities of the ship using PD and fuzzy PID controller. Since both controllers set the ship's forward velocity to 8m/s, it remains constant at 8m/s. Furthermore, the lateral velocity does not occur in any of the sections except for alter course. There was no significant difference in the velocities of the ships between the two controller.
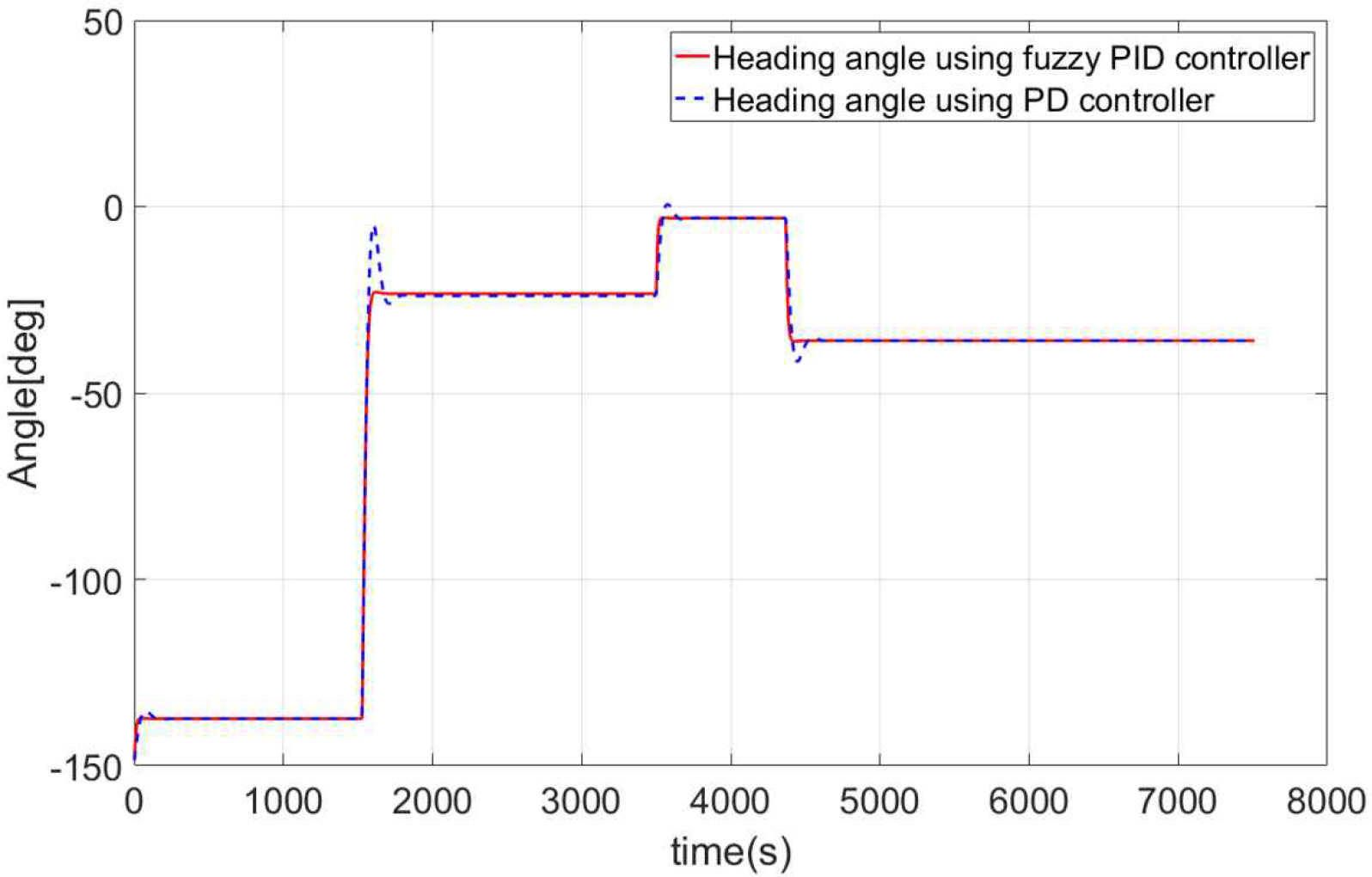
However, there is a big difference in the ship's heading angle. An illustration of the ship's heading angle using both controllers is shown in Fig. 10. With the PD controller, a lot of overshoot can be observed in the alter course section, and it takes a significant amount of time for the ship to stabilized.
Conversely, when using a fuzzy PID controller, almost no overshoot is observed regardless of the size of the angle of the alter course, and the settling time is fast, allowing for fast alter course. If there is a lot of overshoot as in the case of the PD controller the ship could deviate from its set route.
Fig. 11 is the simulation result of the rudder angle used to control a real ship. The rudder angle simulation results also confirm that the fuzzy PID controller performs well. If the rudder changes roughly, for example, with a PD controller, this will also be factor in increasing the amount of fuel that is used to control the rudder. In contrast, fuzzy PID controllers can smoothly change the rudder angle, which can further reduce the energy loss of the ship. The reason why velocity-type fuzzy PID controller perform so well is that they can optimally vary the gain value in real time according to the fuzzy control rules. In addition, since the control output is expressed in incremental form, the effect of overshoot can be greatly attenuated.
In this study, we addressed the problem of determining a shipŌĆÖs route and a route following control technique that can accurately follow the set route. This study is meaningful in that it proposes a method of generating a ship route using DQN and connects the route following using a velocity fuzzy controller.
The targeted route in this study was to depart from Busan port and arrive at the pilot boarding place of the Ulsan port. To ensure the safety of ships, UKC values were derived based on ship specifications to designate non-navigable areas, and navigation chart information was used to ensure that ship operation regulations were met. Under these conditions, a route for the ship was automatically generated. And through the establishment of the experimental environment, it was confirmed that the rewarding area could be passed and it could not pass through the penalty areas. The route initially generated using DQN had the total distance of 66.22 km and 81 way points, but the final route was derived by simplifying it to the total of 55.67 km and 3 way points using the Douglas-Peucker algorithm.
After that, a velocity-type fuzzy PID controller was designed and simulated using a target ship model to accurately follow the route. The PD controller was found to have a lot of overshoot during the alter course and took a considerable amount of time to stabilize the ship. Linear controllers such as PD controllers cannot change the gain value once it has been determined. However, velocity-type fuzzy PID controllers can schedule the gain value in real time according to fuzzy control rules to realize optimal control performance. Therefore, it was confirmed that the control performance of a rudder angle controlling a real ship is superior to that of a PD controller, enabling an accurate and fast-changing route following control.
However, this study has the following limitations. Reinforcement learning requires constructing an experimental environment very similar to the real world. Otherwise, it is very difficult to apply the algorithm in practical situations. It is possible to generate an accurate route based on DQN only when dynamic sea state information is utilized through real-time sensing and data transmission. Therefore, in the future, research that can build an experimental environment in real-time using dynamic sea state information is needed. In addition, it is necessary to conduct comparative research on route generation performance with algorithms such as the deep deterministic policy gradient, A3C, and D* lite.
Acknowledgments
This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean Government (Ministry of Science and ICT) (No. 2022R1C1C2010897).
Fig.┬Ā2.
Fuzzification algorithms; (a) input fuzzification algorithm; (b) output fuzzification algorithm for fuzzy control block 1; (c) output fuzzification algorithm for fuzzy control block 2

Fig.┬Ā3.
The data reflected in the environment for route generation and the structure of the Deep Q-Network
Table┬Ā1.
Specifications of a target ship
| Parameter | length/volume |
|---|---|
| L(m) | 171.8 |
| Lpp(m) | 160.93 |
| T(m) | 8.23 |
| B(m) | 23.17 |
| Ōłć (m3) | 18541 |
Table┬Ā2.
Fuzzy control rule
Table┬Ā3.
Parameter and reward values
References
[1] Chen, C., Chen, X. Q., Ma, F., Zeng, X. J. and Wang, J.(2019), ŌĆ£A knowledge-free path planning approach for smart ships based on reinforcement learningŌĆØ, Ocean Engineering, Vol. 189, pp. 106299.

[2] Davidson, K. S. M. and Schiff, L. I.1946), Turning and course keeping qualities transactions of SNAME..
[3] Guo, S., Zhang, X., Du, Y., Zheng, Y. and Cao, Z.(2021), ŌĆ£Path planning of coastal ships based on optimized DQN reward functionŌĆØ, Journal of Marine Science and Engineering, Vol. 9, No. 2, pp. 210.

[4] He, S., Tan, S., Xu, F. and Wang, P.(1993), ŌĆ£Fuzzy self-tuning of PID controllersŌĆØ, Fuzzy sets and systems, Vol. 56, pp. 37-46.

[5] Kim, C., Park, K. W., Kim, T. S. and Lee, M. K.(2009 ŌĆ£Study on model-based control for the roll motion of an underwater robotŌĆØ, Journal of navigation and port research, Vol. 33, No. 5, pp. 323-330. (in Korean).

[6] Kim, D., Lee, C. and Yim, J.(2023 ŌĆ£An Evaluation Technique for the Path-following Control Performance of Autonomous Surface ShipsŌĆØ, Journal of Navigation and Port Research, Vol. 47, No. 1, pp. 10-17. (in Korean).
[7] Kim, H. T. and Yang, Y. H.(2019 ŌĆ£A review of human element issues of remote operators on maritime autonomous surface shipsŌĆØ, Journal of navigation and port research, Vol. 43, No. 6, pp. 395-402. (in Korean).
[8] Kim, J. H. and Oh, S. J.(2000), ŌĆ£A fuzzy PID controller for nonlinear and uncertain systemsŌĆØ, Soft computing, Vol. 4, pp. 312-129.

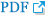
[9] Kim, M. K., Kim, J. H. and Choi, J. K.(2018 ŌĆ£A fuzzy PID autopilot and path following using fuzzy disturbance estimator for a shipŌĆØ, Journal of the korean society of marine engineering, Vol. 42, No. 1, pp. 49-57. (in Korean).

[10] Kim, S., Jeon, H. and Y., K.(2021), ŌĆ£Simplified rule-based strategy control for electric propulsion systemŌĆØ, Journal of advanced marine engineering and technology, Vol. 45, No. 6, pp. 380-385.

[11] Kwak, S. and Choi, B. J.(2018), ŌĆ£Defuzzification scheme and its numerical example for fuzzy logic based control systemŌĆØ, Journal of korean institute of intelligent system, Vol. 28, No. 4, pp. 350-354.

[12] Lee, H. T., Choi, H. M., Lee, J. S., Yang, H. and Cho, I. S.(2022a), ŌĆ£Generation of ShipŌĆÖs Passage Plan Using Data-Driven Shortest Path AlgorithmsŌĆØ, IEEE Access, Vol. 10, pp. 126217-126231.

[13] Lee, J. S., Lee, H. T. and Cho, I. S.(2022b), ŌĆ£Maritime traffic route detection framework based on statistical density analysis from AIS data using a clustering algorithmŌĆØ, IEEE Access, Vol. 10, pp. 23355-23366.

[14] Lee, K. J., Lee, C. M. and Y, H. K.(2004 ŌĆ£Modeling and simulation of a ship with anti-rolling devices in wavesŌĆØ, Journal of navigation and port research, Vol. 28, No. 4, pp. 347-352. (in Korean).

[15] Lee, W., Yoo, W., Choi, G. H., Ham, S. H. and Kim, T. W.(2019 ŌĆ£Determination of optimal route in coastal sea considering sea state and under keel clearanceŌĆØ, Journal of the society of naval architects of korea, Vol. 56, No. 6, pp. 480-487. (in Korean).
[16] Lie, C., Mao, Q., Chu, X. and Xie, S.(2019), ŌĆ£A-star algorithm considering water current, traffic separation and berthing for vessel path planningŌĆØ, Applied science, Vol. 9, No. 6.
[17] Logan, C., Jeff, C., Yisong, Y. and John, P. O.(2021), ŌĆ£Using deep reinforcement learning to reveal how the brain encodes abstract state-space representations in high-dimensional environmentsŌĆØ, Neuron, Vol. 109, No. 4, pp. 724-738.



[18] Nam, S. K. and Yoo, W. S.(1994), ŌĆ£Fuzzy PID control with accelerated reasoning for DC servo motorsŌĆØ, Engineering application of artificial intelligent, Vol. 7, pp. 559-569.

[19] Novac, V., Rusu, E., Gasparotti, C. and Stavarache, G.(2020), ŌĆ£Ship routing in the black sea based on Dijkstra algorithmŌĆØ, In Proc. SGEM Int. Multidisciplinary Sci. GeoConf. EXPO, September 2020, pp. 301-308.

[20] Orsic, J. P., Vettor, R., Faltinsen, O. M. and Soares, C. G.(2016), ŌĆ£The influence of route choice and operating conditions on fuel consumption and CO
2 emission of shipsŌĆØ, Journal of marine science and technology, Vol. 20, pp. 434-457.
[21] Ozturk, U. G., Akdag, M. and Ayabakan, T.(2022), ŌĆ£A review of path planning algorithms in maritime autonomous surface ships: navigation safety perspectiveŌĆØ, Ocean Engineering, Vol. 251.
[22] Roh, M. I.(2013), ŌĆ£Determination of an economical shipping route considering the effects of sea state for lower fuel consumptionŌĆØ, International journal of naval architecture and ocean engineering, Vol. 5, No. 2, pp. 246-262.

[23] Roland, S. B.(1992), ŌĆ£An intelligent integrated ship guidance systemŌĆØ, IFAC proceedings volumes, Vol. 25, No. 3, pp. 199-208.

- TOOLS
-
METRICS

-
- 0 Crossref
- 0 Scopus
- 798 View
- 14 Download
- Related articles
-
A Study on the Fabrication of the 4 Port In-Phase High Power Combiner2002 August;26(3)
A Study on the Strategic Development Plan of the Freight Forwarding Industry in Korea2007 June;31(5)
A Study on the Radar Image Generation Method for Ship Handling Simulator2006 September;30(7)





 PDF Links
PDF Links PubReader
PubReader ePub Link
ePub Link Full text via DOI
Full text via DOI Download Citation
Download Citation Print
Print