원형 기반 선박 충돌 피항 모델에 기반한 정보 교환 분산알고리즘 성능 비교 분석
Comparison and Analysis of Information Exchange Distributed Algorithm Performance Based on a Circular-Based Ship Collision Avoidance Model
Article information
Abstract
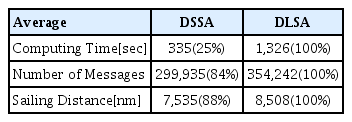
본 연구에서는 선박 간 정보 교환에 기반한 분산지역탐색 알고리즘과 분산확률탐색 알고리즘의 성능을 비교, 분석하고자 한다. 분산알고리즘은 선박 간 정보 교환을 기반으로 하여 최적의 피항 경로를 탐색할 수 있는 방법이다. 분산지역탐색알고리즘은 이웃 선박 중 비용 감소가 최대가 되는 선박만이 다음 예상 위치를 바꿀 수 있도록 해당 선박이 우선권을 가진다. 분산확률탐색알고리즘은 일정 확률로 최적이 아닌 값을 탐색할 수 있도록 하여 새로운 값을 탐색할 수 있도록 한다. 선박 간 충돌 피항 실험은 원형 기반 선박 충돌 피항 모델을 활용하였다. 실험 방법은 원형에 기반하여 원의 중심에서 같은 거리에 떨어진 선박을 2척부터 50척까지 증가시키면서 분산 지역 탐색알고리즘과 분산확률탐색알고리즘을 시뮬레이션 하였다. 실험 평가 방법은 각 알고리즘의 계산 소요 시간, 항행 거리, 메시지 교환 횟수를 비교 분석하였다. 실험 결과 DSSA는 DLSA에 비해 계산시간은 25%, 항행 거리는 88%, 메시지 교환 횟수는 84%를 기록하였다.
Trans Abstract
This study compared and analyzed the performance of a distributed area search algorithm and a distributed probability search algorithm based on information exchange between ships. The distributed algorithm is a method that can search for an optimal avoidance route based on information exchange between ships. In the distributed area search algorithm, only a ship with the maximum cost reduction among neighboring ships has priority, so the next expected location can be changed. The distributed stochastic search algorithm allows a non-optimal value to be searched with a certain probability so that a new value can be searched. A circular-based ship collision avoidance model was used for the ship-to-ship collision avoidance experiment. The experimental method simulated the distributed area search algorithm and the distributed stochastic search algorithm while increasing the number of ships from 2 to 50 that were the same distance from the center of the circle. The calculation time required for each algorithm, sailing distance, and number of message exchanges were compared and analyzed. As a result of the experiment, the DSSA(Distributed Stochastic Search Algorithm) recorded a 25% calculation time, 88% navigation distance, and 84% of number of message exchange rate compared to DLSA.
1. 서 론
1.1. 연구 배경 및 목적
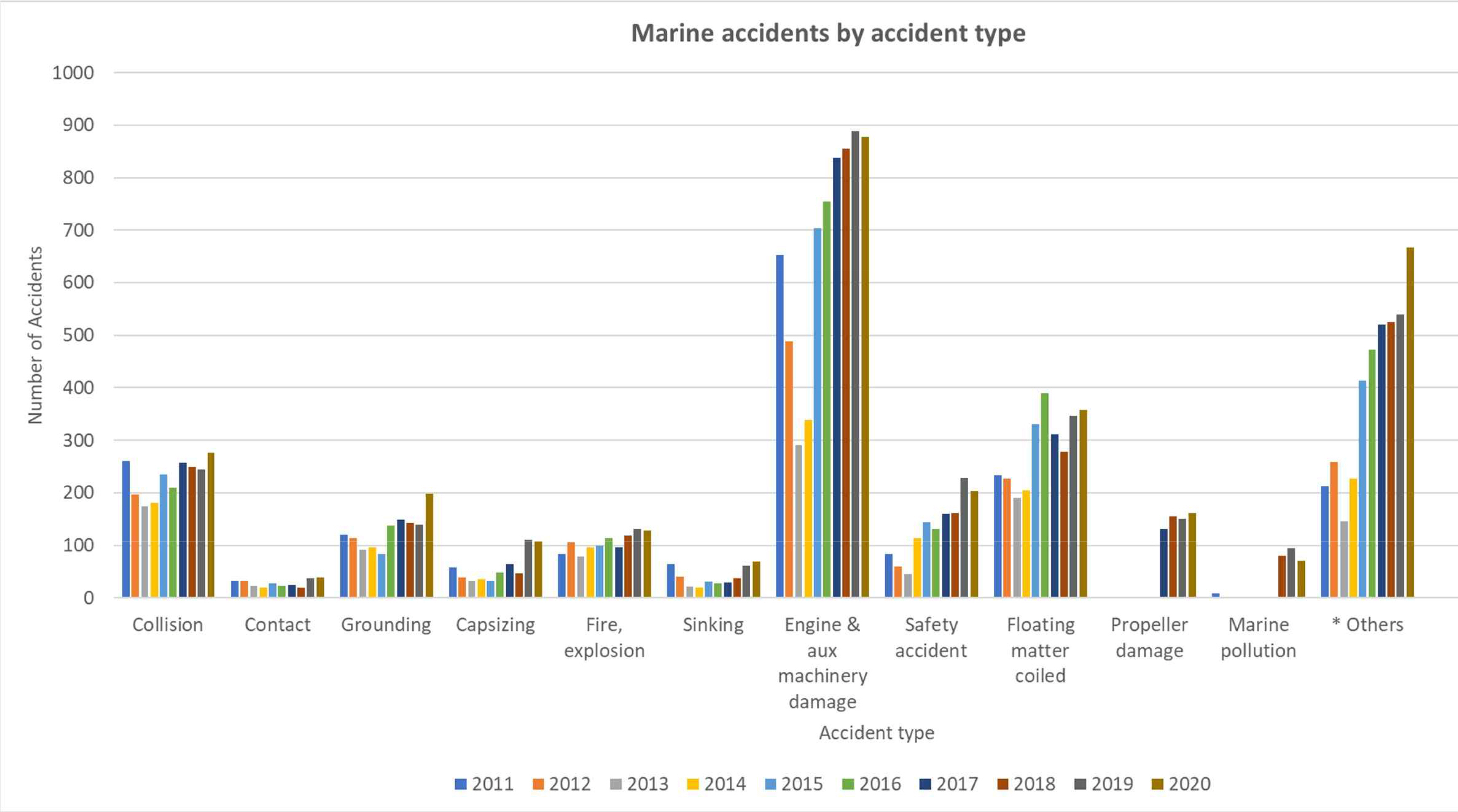
과거에 비해 선박의 운항 환경은 빠르게 변화하고 있다(Kim and Jang, 2019, Korea Autonomous Surface Ship Project, 2023). 그러나 기술의 발전에도 불구하고 Fig. 1과 같이 선박 간 충돌 사고는 줄지 않고 연간 200건 이상 발생하고 있다(Korea Maritime Safety Tribunal, 2023). 이는 엔진 고장, 부유물에 의한 감김 사고에 이어 3번째로 많은 선박 사고이다. 선박 충돌 사고의 주요 원인으로 인적 요인을 들 수 있다. 항해사의 판단 실수나 긴 운항 시간으로 인한 피로 및 집중력 저하로 인한 오작동 등이 문제가 될 수 있다(Kim, 2017).
이를 방지하기 위해 자율운항 기술이 빠르게 발전하고 있다(Korea Autonomous Surface Ship Project, 2023). 인간의 개입 없이 안전한 항행이 가능하도록 하여 인적 요인으로 인한 사고 가능성을 줄일 수 있다. 즉 선박 주변 상황을 정확히 감지하고 해석하여 사전에 충돌을 예측할 수 있다. 예를 들어 선박 접안 시 라이더를 활용하여 정확한 위치 정보 취득이 가능하다(Wang and Zhang, 2022).
선박 충돌 방지를 위해 인공지능 및 머신 러닝을 활용하여 선박 운항 데이터를 수집, 분석하여 패턴을 파악하여 충돌 위험을 예측하는 기술을 개발중이다(Chun, D. et al. 2021, Sun, Z. et al. 2023, Zhai, P. et al. 2022).
또한 자율운항선박 기술 중 선박 간 통신 및 협력은 매우 중요하다. 왜냐하면 상대 선박의 다음 위치를 정확히 알지 못하고 본선의 예측만으로 피항할 경우, 충돌 위험이 존재하기 때문이다. 따라서 두 선박 간 상호간의 피항 의도를 명확히 알기 위한 방법이 필요하다.
본 연구에서는 선박 간 통신 및 협력에 기반한 분산지역탐색알고리즘과 분산확률탐색알고리즘의 작동 방법 및 두 알고리즘의 성능을 비교 분석하고자 한다.
1.2 연구 방법
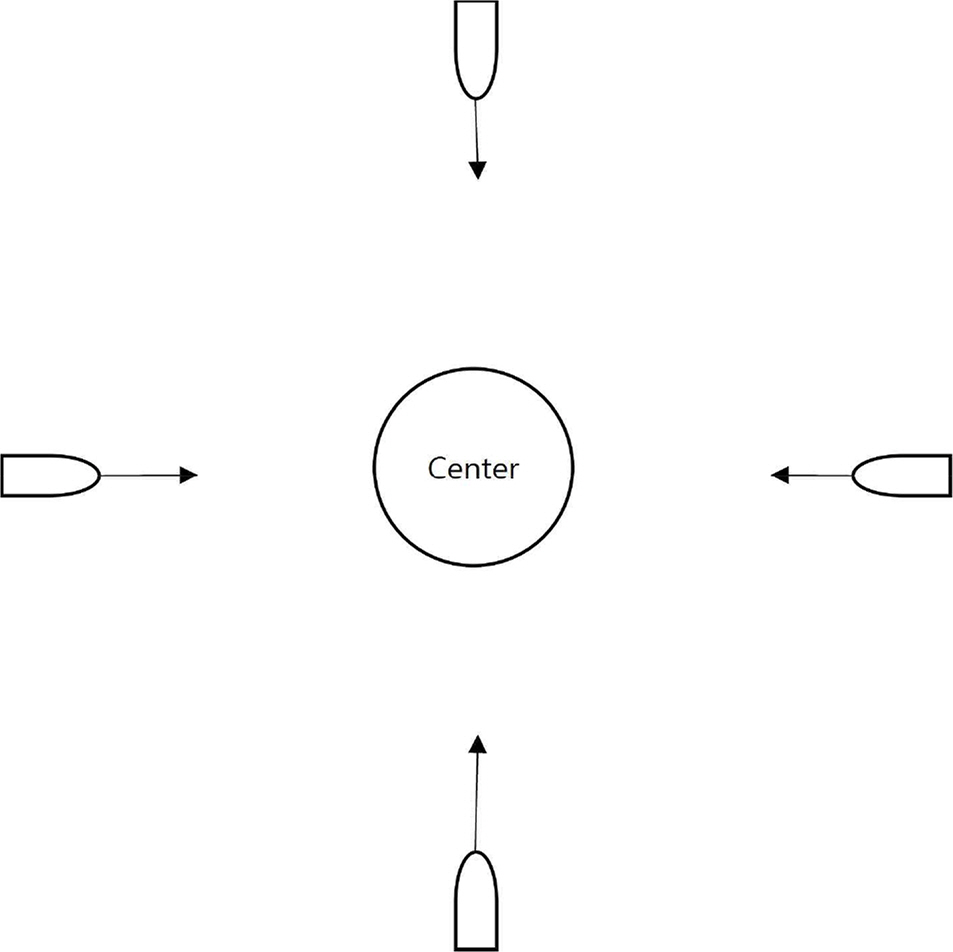
본 연구는 원형 기반 충돌 피항 실험 환경에서 선박의 척수를 증가시켜가며 분산지역탐색알고리즘과 분산확률탐색알고리즘의 성능을 비교 분석하는데 목적이 있다. 모든 선박은 원을 중심으로 같은 거리의 가장자리에서 출발하여 원의 중심을 지나 반대편 목적지를 향하도록 설정하였다. 원형 기반 충돌 피항 모델을 선정한 이유는 다음과 같다.
- 선박 간 상대적 위치 관계가 동일하다. 즉 특정 선박이 특수한 환경에 처하지 않도록 하여 모든 선박이 동일한 조건에서 실험 수행이 가능하다.
- 각 선박은 원의 중심을 지나 반대편에 목적지를 설정하도록 하였다. 즉 모든 선박이 원의 중앙에서 조우하도록 하여 가장 복잡한 상황 재현이 가능하도록 하였다.
두 알고리즘의 계산 소요 시간, 항행 거리, 메시지 교환 횟수를 비교 및 분석하였다. 연구의 순서는 다음과 같다. 2장에서는 분산 알고리즘을 소개한다. 3장에서는 두 알고리즘을 시뮬레이션을 통해 성능을 비교, 분석한다.
1.3 선행 연구
선박 충돌 피항을 위한 중앙집중식의 경우, 대표적으로 선박교통관제사(VTSO, Vessel Traffic Service Operator)가 선박의 항행 경로를 통제하는 방법이 있다. Lee and Song(2017)은 선박 충돌 위험도를 산출하기 위해 VTS 관점에서 선박 조우 상황에 따른 위험, 근접 거리, VTSO의 위험 태도를 반영하였다. Pak, C. et al.(2014)는 VTS 중심의 선박 간 경로 교환을 위한 방법을 제안하였다. Lee and Song(2018a)은 선박 간 충돌 위험 상황에서 해상 교통 관제사의 상황 인식에 따른 위험 태도를 분석하였다. Lee and Song(2018b)는 정박선 간 적정한 영역 감시를 결정하기 위해 방법을 제안하였다. Oh, J. et al.(2018)는 AIS 데이터를 활용하여 통항 패턴 학습 및 학습된 모델과 실제 데이터의 비교를 통해 이상치를 계산하여 이상 거동 선박을 판별하였다. 그러나 위와 같은 방법은 모든 정보가 특정 그룹에 집중되어 있으며 해당 그룹에 문제가 발생 될 경우, 정상적으로 작동하지 못할 가능성이 있다.
이에 반해 다수 선박 간 정보 교환을 통한 방법이 제안되고 있다. Liu, Y. et al.(2007)는 선박 충돌 회피 의사결정 연구를 위한 다중 에이전트 기반 시뮬레이션 시스템을 제안하였다. 4가지의 에이전트 모델(Control_Agent, Union_Agent, Ship_Agent 및 VTS_Agent)을 활용하여 인간, 선박 및 VTS 의 행동을 모델링하기 위해 각각의 에이전트 프레임워크를 사용하여 모델을 개발하였다. 제안된 다중 에이전트 기반 시뮬레이션 시스템은 충돌 방지를 위한 다중 대상 발생 문제 및 다양한 의사 결정 방법을 제공할 수 있다. 그러나 복잡한 상황에서의 성능 분석 방법에 대한 언급이 없다. Hornauer and Hahn(2013)는 좁은 수로와 넓은 바다에서 신뢰할 수 있는 충돌 방지를 제공하기 위해 AIS에 기반하여 각 선박이 협상에 참여하여 주어진 제약 내에서 각 선박은 최적의 피항 경로를 찾기 위해 노력한다. 그러나 AIS가 없는 선박의 경우, 이러한 방법의 적용이 힘들다는 단점이 있다. Ferranti(2018)는 비선형모델 예측 제어를 기반으로 다중 객체 궤도 계획 및 조정 방법을 제안하였다. 각 객체는 이웃 객체와 정보 교환을 통해 최적의 피항 경로를 탐색할 수 있다. 그러나 계산하기 위해 일정 시간 정지해야 한다는 단점이 존재한다. Yang(2020)는 네트워크를 학습시켜 선박의 움직임을 고려한 협력 충돌 방지 메커니즘을 제안하였다. 선박의 동적 정보를 학습하여 안전한 상태를 예측할 수 있는 AI 기반 선박 네트워크 움직임 모델을 설계하였다. 시뮬레이션 결과 제안된 접근 방식이 유전자 알고리즘의 안정성을 향상시키고 협력적 충돌 회피를 위한 최적의 안전 경로 계획을 달성할 수 있음을 보여주었다. 그러나 선박 간 정보 교환을 위해 제안된 방법들은 실제 선박에 적용하기 위한 성능에 대한 언급이 부족한 실정이다.
선박 간 정보 교환에 대한 알고리즘에 대한 비교 분석은 부족한 실정이다. 따라서 본 연구에서는 선박 간 정보 교환에 기반한 분산 알고리즘의 성능 실험을 통해 선박 척수 변화에 따른 성능을 비교 분석하고자 한다.
2. 분산 알고리즘
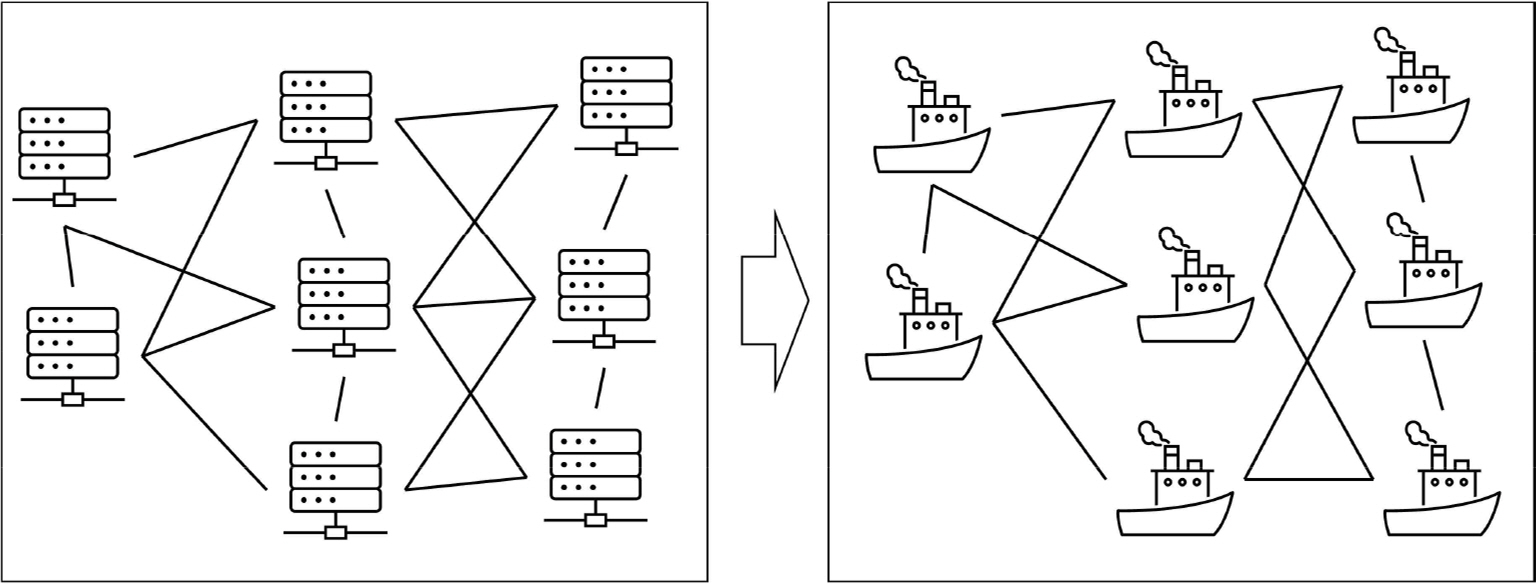
Fig. 2와 같이 분산 알고리즘은 상호 연결된 프로세서로 구성된 하드웨어에서 실행되도록 설계된 알고리즘을 의미한다. 예를 들어 분산 정보 처리, 실시간 프로세서 제어와 같은 분야에서 사용되고 있다. 분산 알고리즘을 선박 충돌 분야에 적용한 분산지역탐색알고리즘과 분산확률탐색알고리즘의 성능을 비교, 분석하고자 한다. 먼저 본 장에서는 분산지역탐색알고리즘(Kim, et al., 2015)과 분산확률탐색알고리즘(Kim, et al., 2017)에서 사용되는 용어에 대해 설명하고자 한다.
2.1 용어 및 정의
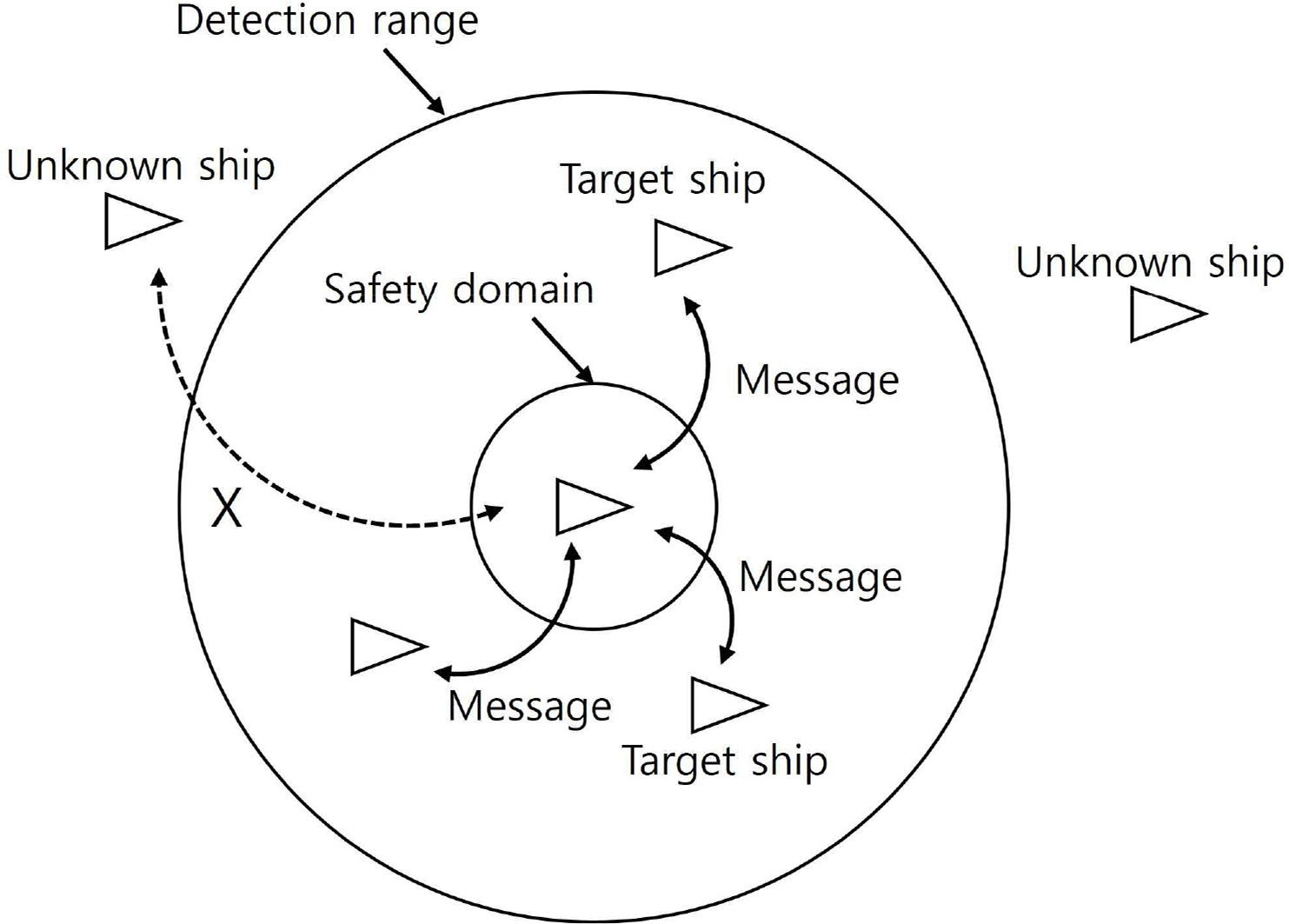
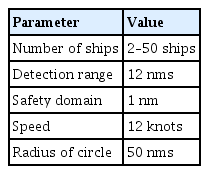
Fig. 3과 같이 원의 중앙에 위치한 삼각형은 본선을 의미한다. 다양한 모형의 safety domain이 제안되고 있으며(Szlapczynski, R. and Szlapczynska, J. 2017) 본선은 원형의 safety domain을 가진다. 시뮬레이션 구현이 용이하기 때문에 원형 기반 safety domain을 선정하였다. 이 safety domain 영역 이내에 상대 선박이 침범하였을 경우, 충돌로 간주한다. 가장 바깥의 원은 detection range로 상대 선박과 정보 교환이 가능한 영역을 의미한다. 이 detection range 내의 선박과는 메시지 교환이 가능하며 이 영역 바깥의 선박과는 메시지 교환이 불가능하다. Table 1은 각 용어에 대한 설명이다.
2.2 분산지역탐색알고리즘(Distributed Local Search Algorithm, DLSA)
DLSA(Kim D. 2015)는 다음 절차와 같이 작동된다.
Repeat the following procedures until no collision risk
Step 1: Each ship sends its current information to neighbors via ok? messages.
Step 2: Each ship sends possible improvement in collision risk to neighbors via improve messages.
Step 3: The ships with larger improvement than neighbors change their direction (ties are broken by the ship priorities).
즉, 각 선박은 상대 선박과 정보를 교환 후 비용을 가장 많이 줄일 수 있는 방법을 모색 후 가장 크게 비용을 줄이는 선박이 다음 피항 코스를 선택할 수 있는 우선권을 가진다. 이러한 과정을 목적지에 도착할 때까지 반복한다. 여기서 비용이란 상대 선박과의 충돌을 피하기 위해 발생되는 거리와 위험도의 증가를 의미한다(식 2 참조)
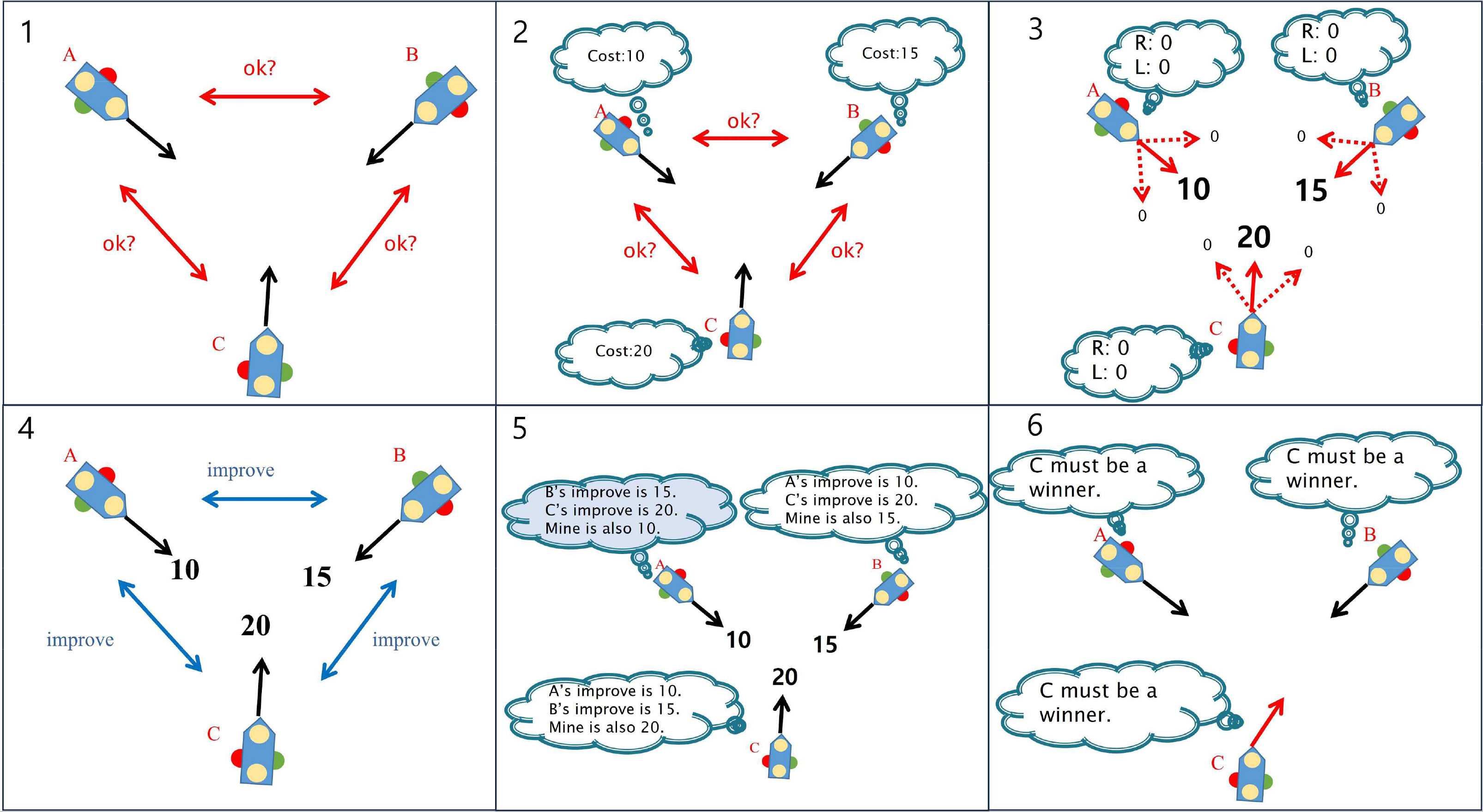
더 자세히 설명하면 Fig. 4와 같이 각 선박은 detection range 이내의 상대 선박과 정보 교환을 실시한다. 이 때 ok? message를 교환한다(1). 이를 기반으로 각 선박은 현재 코스의 비용을 계산한다(2). 현재 상태에서 가장 크게 비용을 낮출 수 있는 코스와의 차이(improvement)를 계산한다(3). 이후 이 improvement를 교환한다(4). 각 선박은 상대 선박의 improvement와 본선의 improvement를 비교(5)하여 가장 큰 선박이 다음 위치를 변경할 수 있는 우선권을 가진다(6).
2.3 분산확률탐색알고리즘(Distributed Stochastics Search Algorithm, DSSA)
DLSA에서는 다음 위치를 결정하는데 있어서 가장 크게 비용을 감소 시킬 수 있는 선박이 다음 위치를 결정하도록 하였다. 이는 모든 선박이 동시에 다음 피항 경로를 결정할 경우, 기존의 상대 선박에 대한 정보와 현재 상대 선박의 정보가 달라지게 되어 다시 충돌이 발생할 가능성이 높다. DSSA는 DLSA와 같이 항상 최적의 피항 경로를 탐색하는 것은 동일하지만 동시에 일정 확률로 최적이 아닌 피항 경로를 선택할 수 있도록 하였다.
Table 2는 실험에 사용된 파라메터에 설정을 의미한다. 선박 척수의 경우, 2척은 충돌 피항이 가능한 최소 척수 이며 50은 컴퓨터 성능을 고려한 최대 척수이다. Detection range는 선박 간 정보 교환이 가능한 거리를 의미한다. 12 nms로 설정한 이유는 실제 항행시 레이더의 레인지를 참고하여 설정하였다. Safety domain은 선박의 안전 영역으로 이 영역 이내에 상대 선박이 들어오지 못하도록 한다. Park, et al.(2010)은 전방 조우시 이격 거리를 4.4L로 제안하였다. 본 연구에서는 선박을 점으로 가정하여 실험을 진행하였으며 400m 선박의 경우, 약 1 nm 정도의 이격 거리가 필요하는 점을 고려하여 safety domain을 1nm로 설정하였다. Speed의 경우 본 연구에서는 벌크선으로 가정하여 실험을 진행하였다. Radius of circle을 50 nms로 설정한 이유는 모든 선박이 초기에 충분한 공간을 가지게 하기 위해 설정하였다.
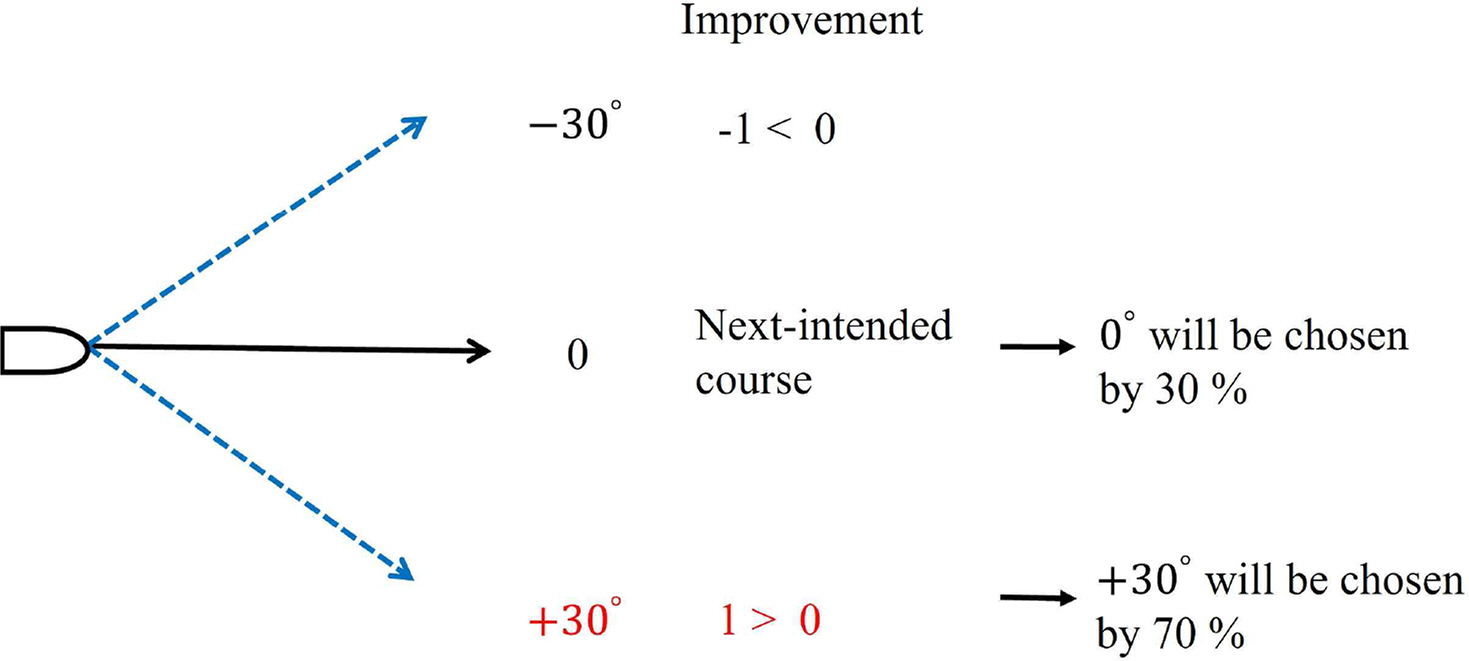
Fig. 5는 DSSA(Kim, 2017)에 의한 피항 방법을 의미한다. 먼저 각 선박은 상대 선박과 ok? message를 교환한다. 이후 각 선박은 현재 상태의 최적 피항 경로를 일정 확률 p만큼 선택하도록 하였으며 일정 확률 1-p만큼 다른 코스를 선택할 수 있도록 하였다. 이때 확률 p는 Fig. 6과 같이 결정된다. Fig. 6은 이해를 위해 선박이 선택할 수 있는 코스를 단순화한 그림으로 실제 실험에서는 {±45°, ±30°, …, 0° ∪ θdestination} 의 20개의 피항 코스를 선택할 수 있다. θdestination 는 목적지를 향하는 코스를 의미한다. DLSA에서는 선박은 현재 상태보다 비용을 감소시킬 수 있는 피항 경로를 100%, 즉 항상 비용 감소가 가장 큰 피항 경로를 탐색하였다. 그러나 DSSA는 비용 감소가 가장 큰 피항 경로를 70%만큼 선택하도록 하였다. 나머지 30%는 임의의 피항 경로를 탐색하도록 하여 새로운 탐색 경로를 찾을 수 있도록 하였다(Kim, 2019).
비용(Cost)과 improvement는 식 (1, 2, 3)에 의해 계산된다.
식 (1)의 CR은 충돌 위험도를 의미한다. T는 timewindow를 의미하며 타 선박을 예측하기 위한 최대 시간을 의미한다. crs와 j는 각각 후보 코스와 상대 선박을 의미한다. self는 본선을 의미한다. 만약 본선이 상대 선박j와 충돌 위험이 있을 경우, 위험도가 계산된다. 충돌 위험이 없을 경우, 0이 된다. 식 (2)는 각 코스별 비용을 계산한다. 먼저 전반부의 항은 식 (1)에 의해 계산된 각 코스별 상대 선박과의 위험도이다. 후반부의 항은 목적지와 코스와의 각도를 의미한다.
식 (3)은 현재 코스의 비용과 다른 코스의 비용의 차이 중 가장 큰 값을 improvement로 결정한다. 즉 현재 코스에서 어떤 코스를 선택해야 가장 크게 비용을 감소시킬 수 있는지를 의미한다.
본 연구에서 다수의 선박은 정보 교환, 즉 상호 약속된 상황을 전제로 충돌 피항을 수행한다. 그러나 COLREG rule 13(Overtaking), 14(Head-on), 15(Crossing)에는 상대 선박과 조우시 가능한 우현 변침을 권고하고 있다(COLREG, 1972). 따라서 다수의 선박이 조우하는 복잡한 상황에서 우현 변침하도록 설정하였다.
3. 시뮬레이션
3.1 실험 환경- 원형 기반 선박 충돌 피항 모델
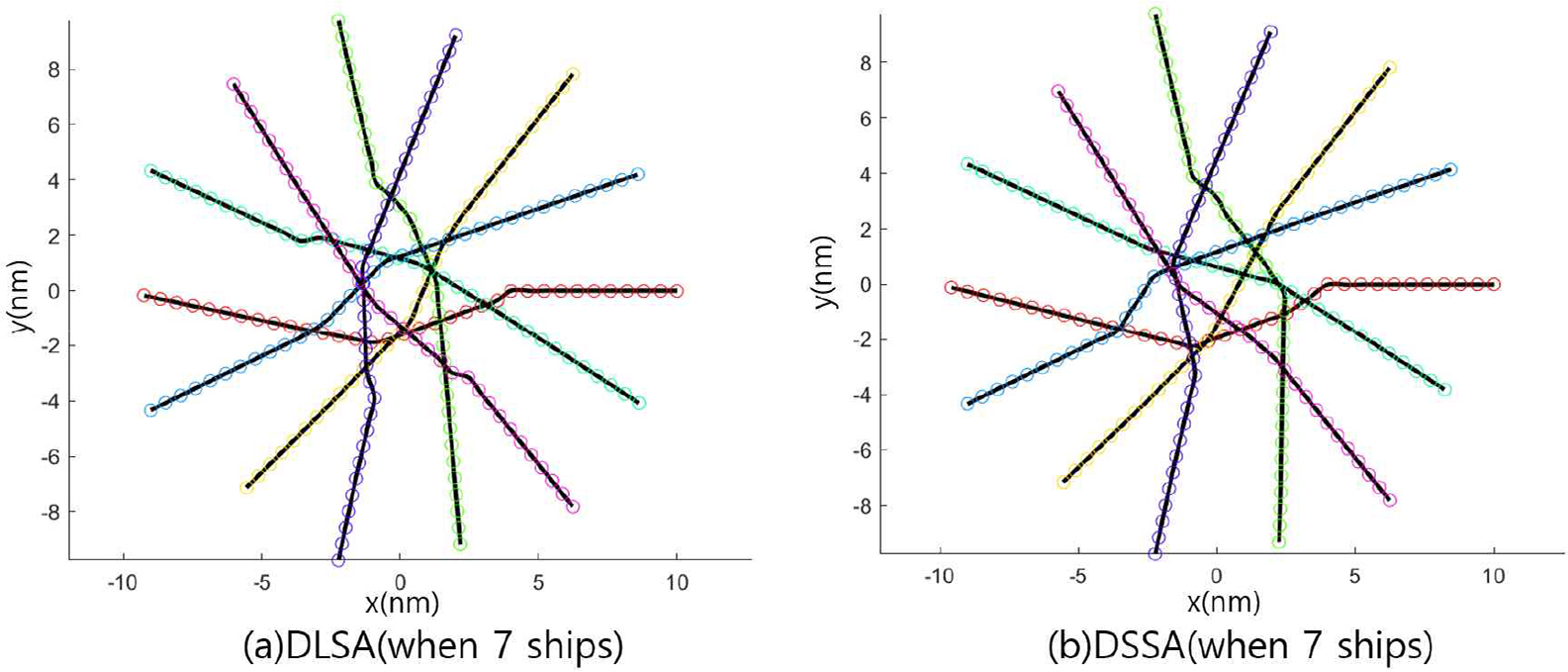
실험 환경은 Fig. 7과 같다. 원형 기반 선박 충돌 피항 모델을 활용하였다. 모든 선박과의 상대적 위치 및 거리가 동일하며 모든 선박이 중앙에서 교차할 수 있도록 하여 가장 복잡한 상황의 재현이 가능하다. Fig. 8은 7척 선박의 경우의 실험 예이다. Fig. 8(a)는 DLSA를 적용한 예이며 (b)는 DSSA를 적용한 예이다.
3.2 분산 알고리즘 피항 실험
3.2.1 Computing time
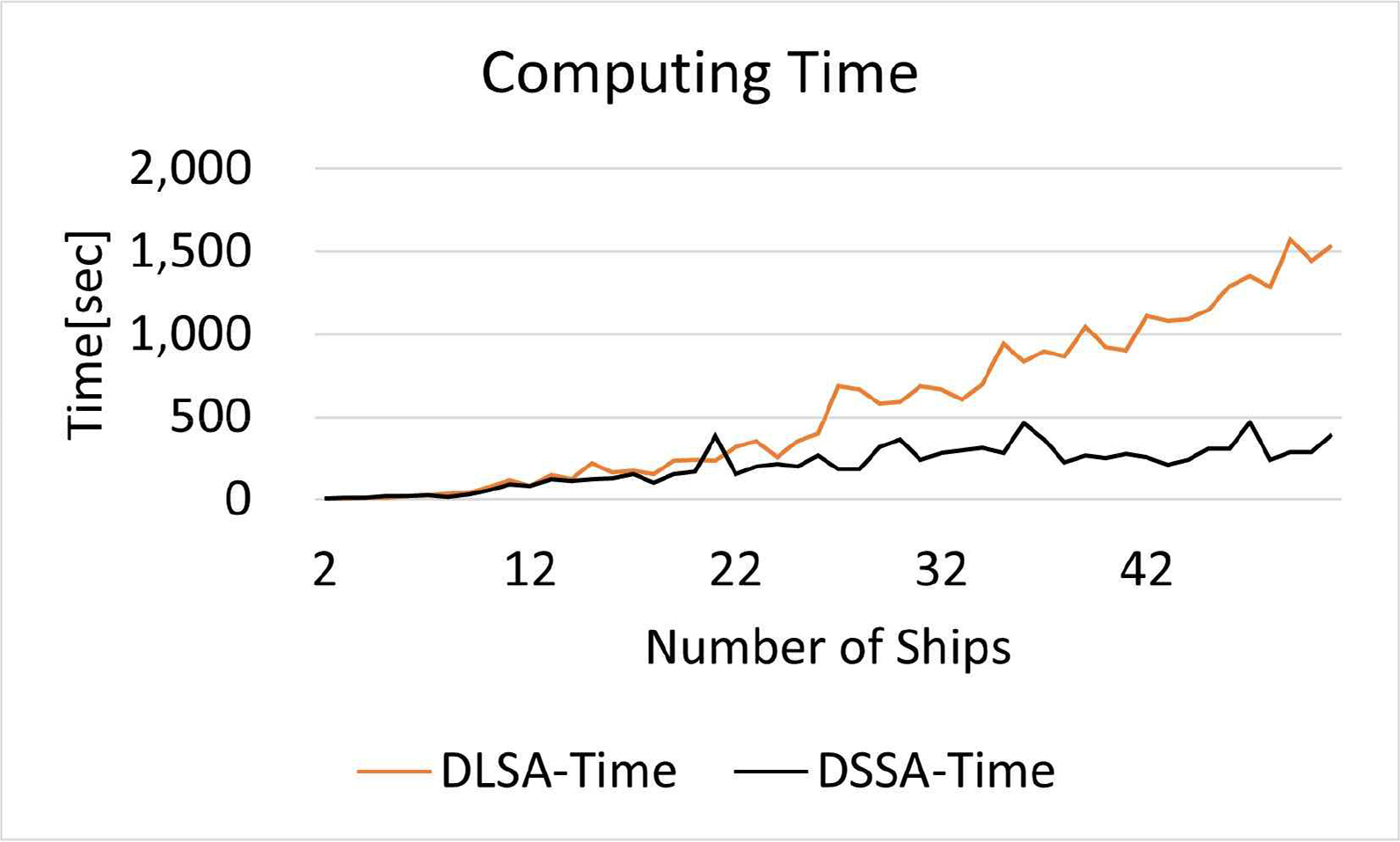
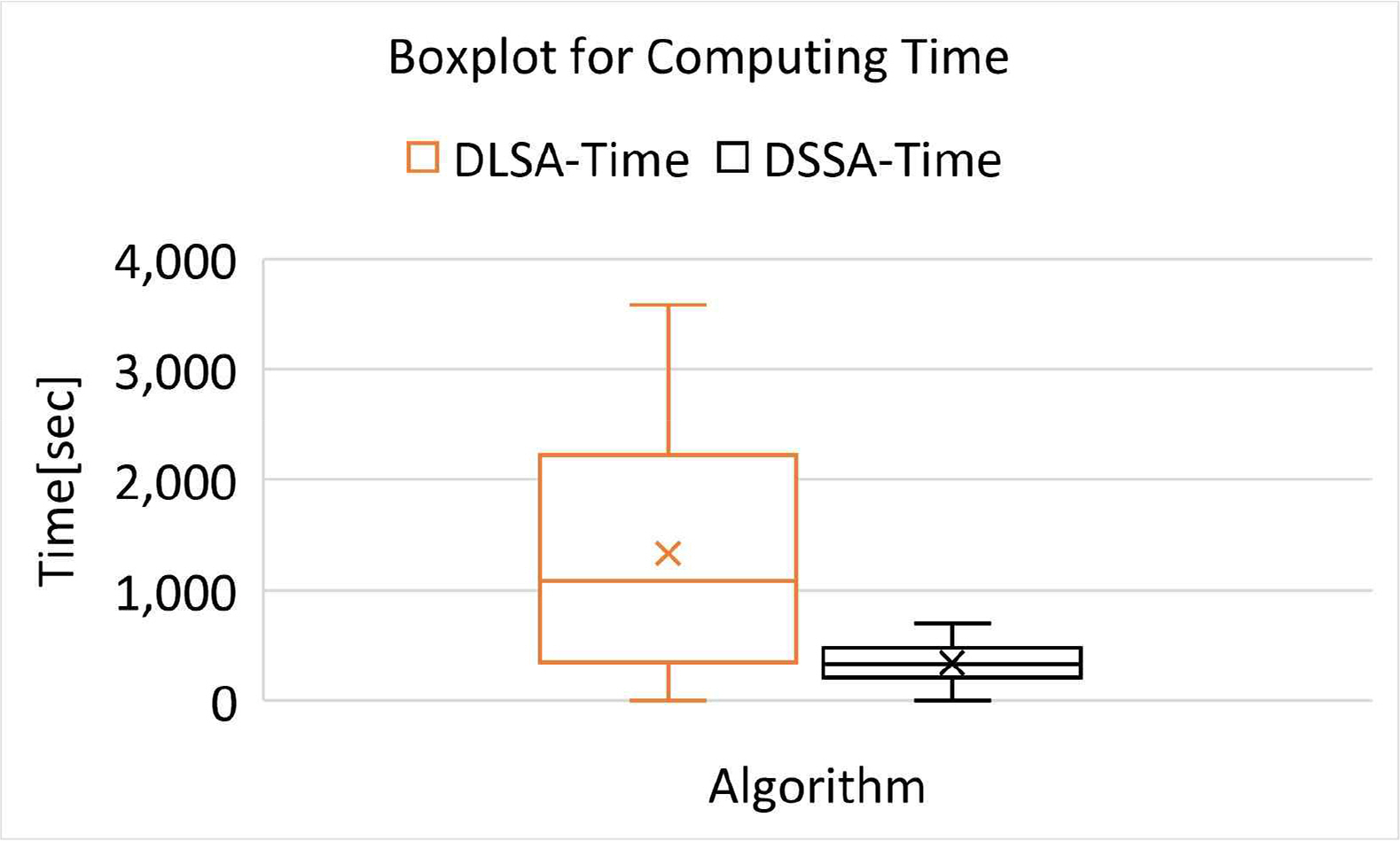
Fig. 9는 선박 척수 증가에 따른 알고리즘의 계산 시간을 의미한다. 검은색 실선은 DSSA, 오렌지색 실선은 DLSA를 의미한다. DLSA는 선박 척수가 증가함에 따라 증가하는 경향을 보였다. 그러나 DSSA의 경우, 크게 증가하지 않고 일정 값으로 수렴함을 보였으며 DLSA에 비해 낮은 값을 기록하였다. Fig. 10은 boxplot로 표시된 DLSA, DSSA의 계산 시간을 의미한다. DSSA는 DLSA에 비해 낮은 평균 및 분산을 보여주었다.
3.2.2 Sailing distance
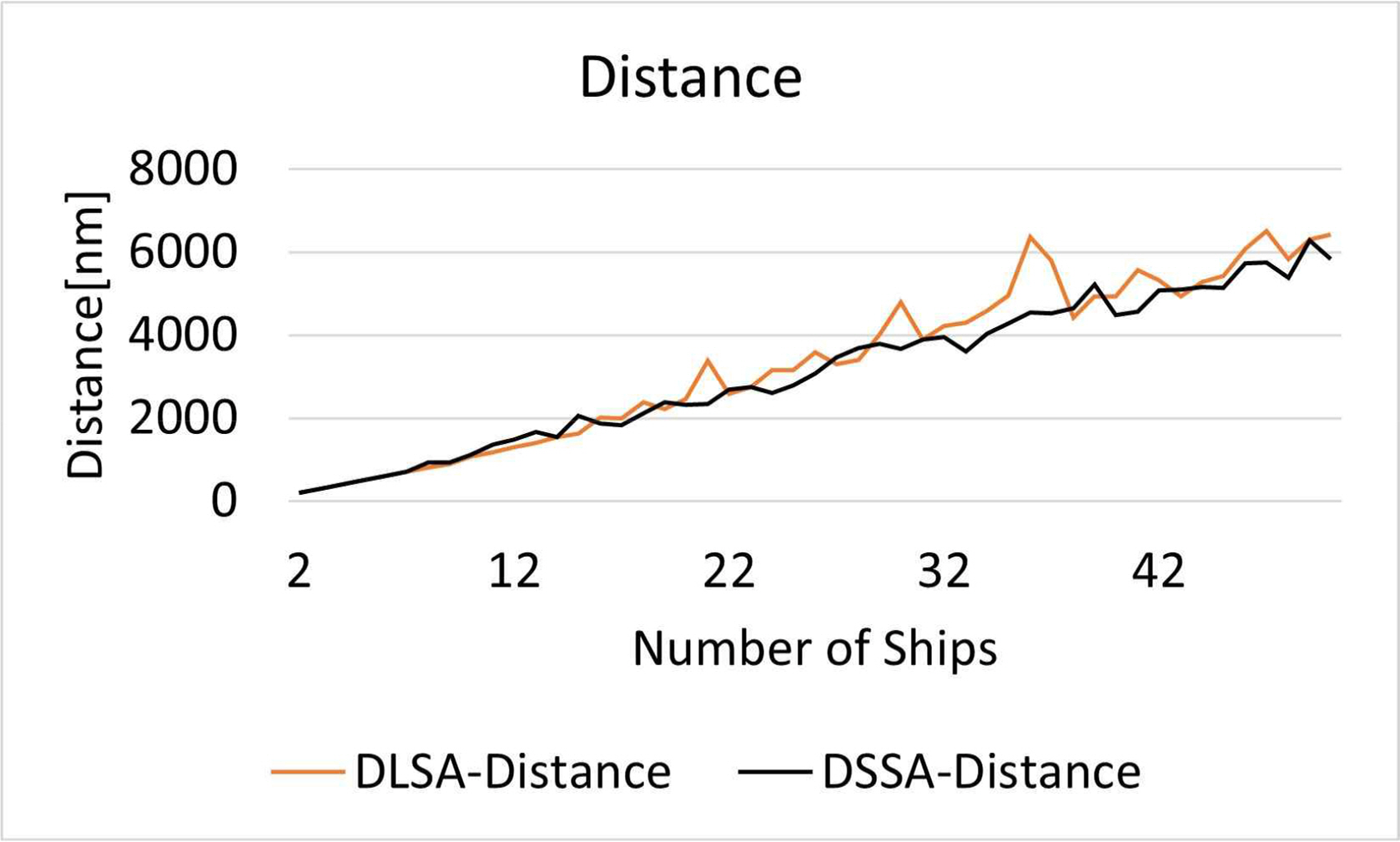
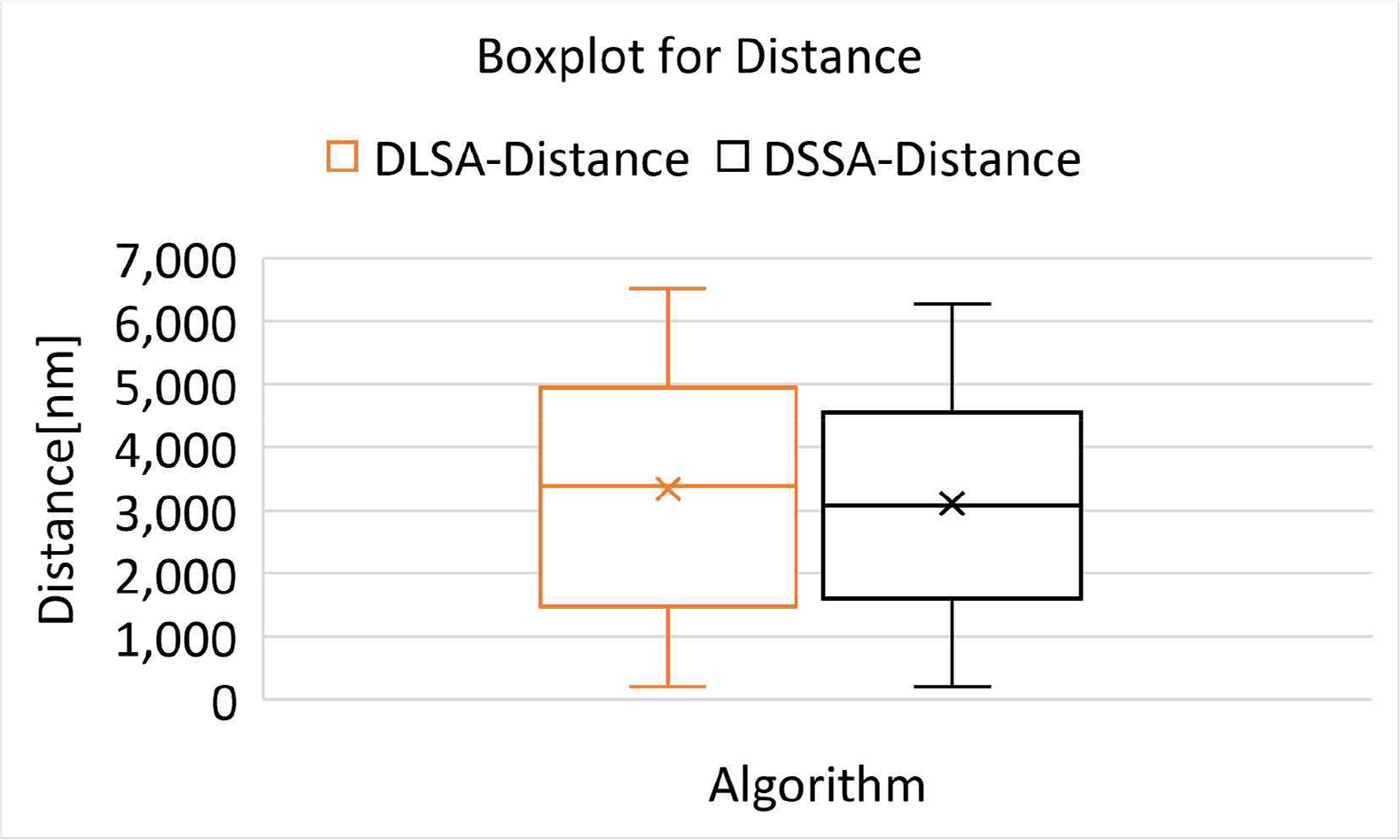
Fig. 11은 선박의 척수에 따른 항행 거리를 의미한다. 검은색 실선은 DSSA, 오렌지색 실선은 DLSA를 의미한다. 선박 척수가 증가할수록 DLSA, DSSA 모두 항행 거리가 증가하는 것을 확인하였다. 동일한 실험 환경에 대해 DSSA가 DLSA보다 작은 항행 거리를 기록하였다. Fig. 12는 boxplot로 표시된 DLSA, DSSA의 항행 거리를 의미한다. DSSA는 DLSA에 비해 낮은 평균 및 분산을 보여주었다.
3.2.3 Number of messages
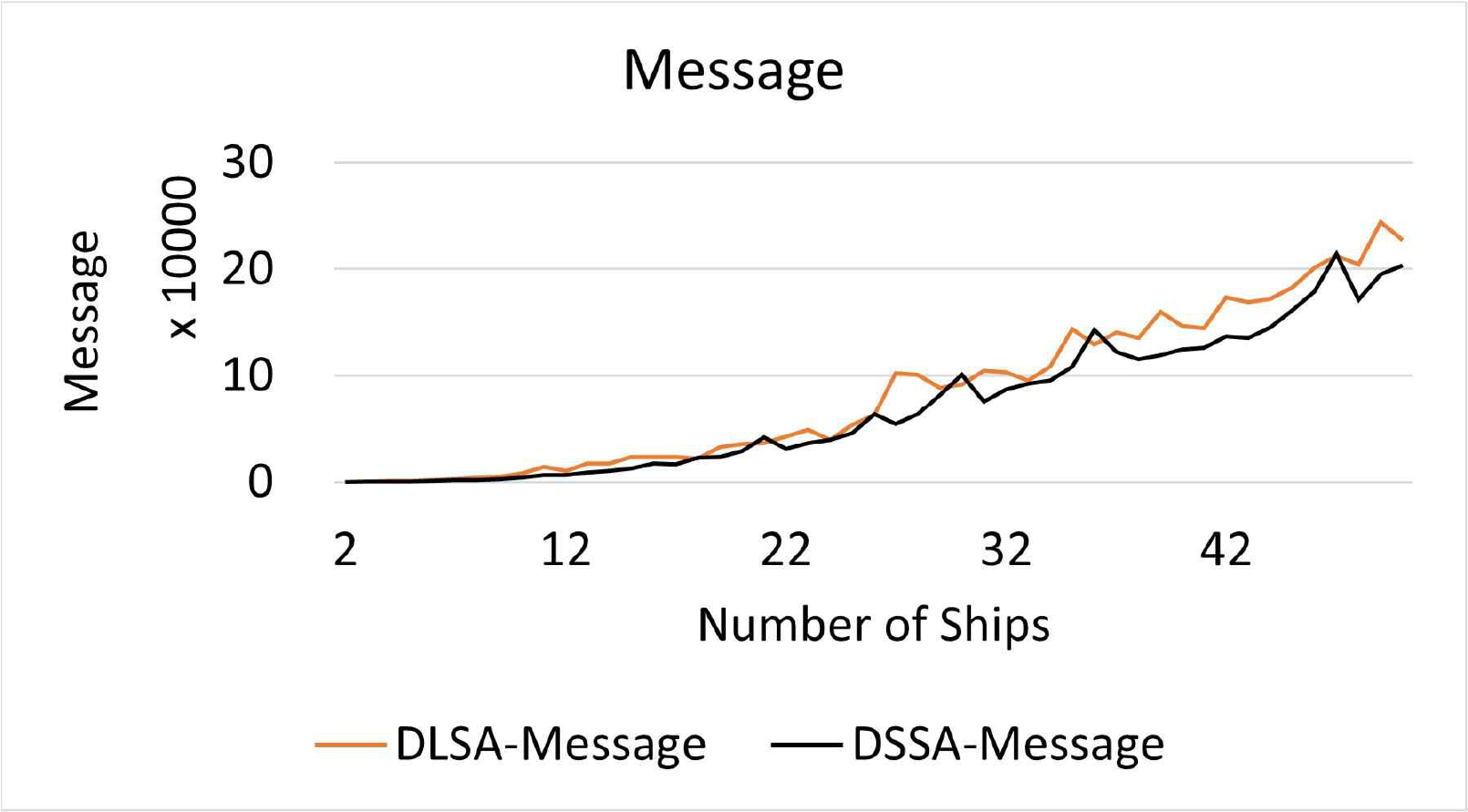
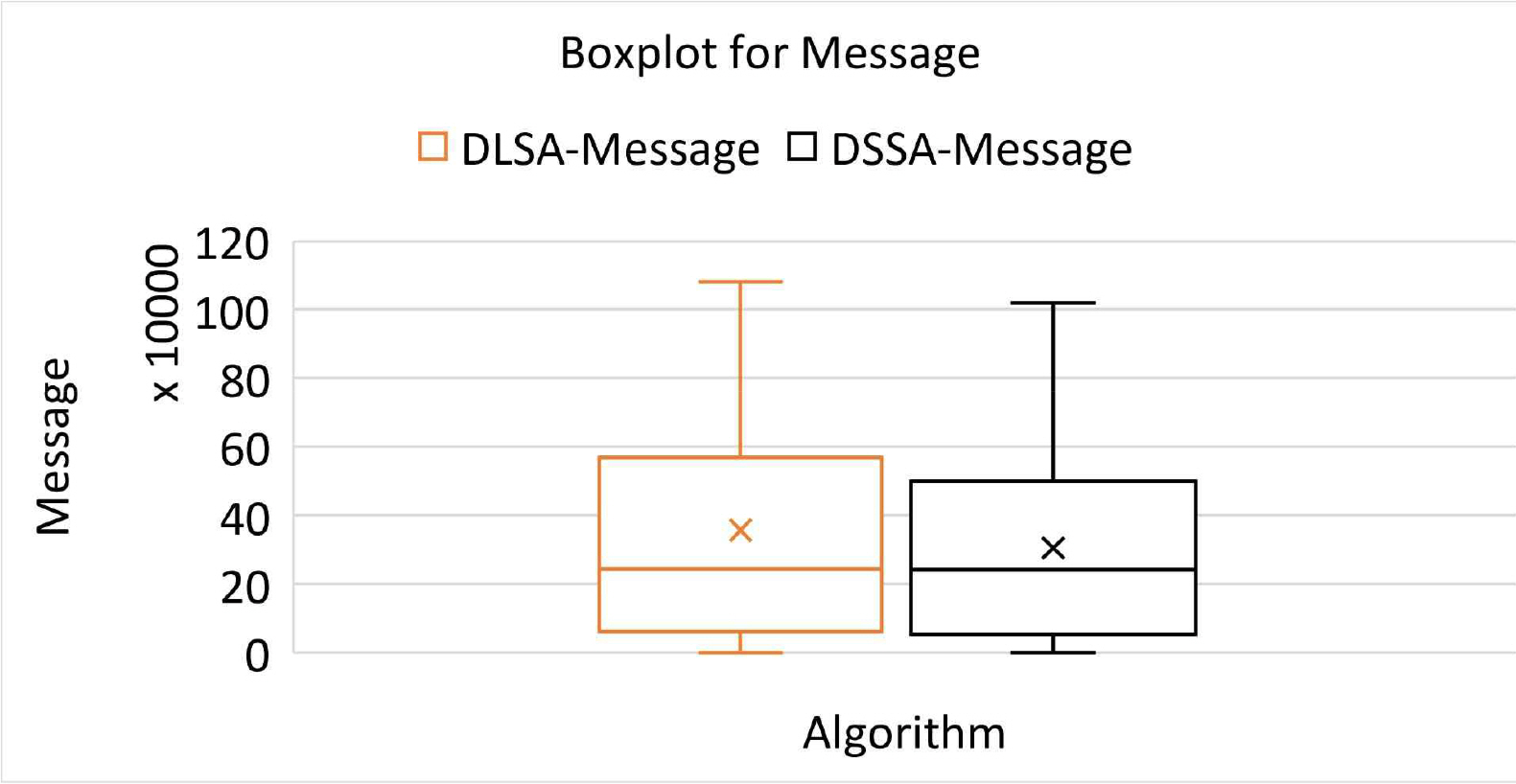
Fig. 13은 선박의 척수에 따른 메시지 교환 횟수를 의미한다. 검은색 실선은 DSSA, 오렌지색 실선은 DLSA를 의미한다. 선박 척수가 증가할수록 DLSA, DSSA 모두 메시지 교환 횟수가 증가하는 것을 확인하였다. 동일한 실험 환경에 대해 DSSA가 DLSA보다 적은 메시지 교환 횟수를 기록하였다. Fig. 14는 boxplot로 표시된 DLSA, DSSA의 메시지 교환 횟수를 의미한다. DSSA는 DLSA에 비해 낮은 평균 및 분산을 보여주었다.
3.3 실험 결과
실험 결과는 Table 3과 같다. 모든 실험에서 DSSA는 DLSA보다 나은 성능을 기록하였다. 특히 계산 시간에서 DSSA는 DLSA에 비해 25%만 소요되었다. 계산 시간은 컴퓨팅 성능과 관련되며 얼마나 빨리 피항 경로 탐색이 가능한지를 의미한다. Number of Messages의 DSSA는 DLSA에 비해 84%를 기록하였다. 이는 선박 간 정보 교환과 관련되며 선박 통신 장비의 성능과 밀접한 관련이 있을 것으로 보인다. Sailing Distance의 경우, DSSA가 DLSA에 비해 88% 작은 값을 기록하였다. 즉 DSSA의 최적 피항 경로가 DLSA에 비해 작음을 의미하며 이는 선박의 항행 거리, 연료 효율과 관련이 있을 것으로 보인다. Fig. 15는 Table 3의 수치를 그래프로 표시하였다.
4. 결 론
기존 연구의 경우, 정보 교환에 관한 구체적인 방법에 대한 언급이 없거나 타선은 초기 설정에 따라서만 움직이며 본선만 피항을 하는 연구 환경이 많았다. 즉 실제로는 본선의 움직임에 따라 상대 선박 또한 피항 경로를 탐색하기 위해 노력할 것이며 이러한 결과는 다시 본선의 피항에 영향을 미친다. 이러한 점을 극복하기 위해 본 연구에서는 선박 간 정보 교환에 기반한 분산지역탐색알고리즘과 분산확률탐색알고리즘의 성능을 비교, 분석하였다.
본 연구의 내용을 요약하면 다음과 같다.
· 선박 간 충돌 피항을 위해 원형 기반 충돌 피항 모델을 활용하였다.
· 선박 간 충돌 피항을 위해 분산지역탐색알고리즘과 분산확률탐색알고리즘의 작동 방법 및 성능을 비교, 분석하였다.
· 실험은 2척에서 50척까지 선박의 척수를 증가시키면서 원의 중심에서 모든 선박이 같은 거리에서 떨어져 원의 중앙을 지나 반대편의 목적지로 향하도록 하였다.
· 모든 선박은 일정 거리(safety domain) 이내에는 상대 선박이 침입하지 못하도록 하였으며 일정 거리(detection range) 이내의 선박과 정보교환이 가능하도록 설정하였다.
· 실험 결과 DSSA가 DLSA에 비해 모든 부분에서 우위를 기록하였다. DSSA는 DLSA에 비해 계산 시간의 경우, 25%, 메시지 교환 횟수의 경우, 84%, 항행 거리의 경우, 88%를 기록하였다.
추후 연구 과제로 원형 기반 이외의 다양한 모형에서의 충돌 피항이 필요하며 본 연구에서는 선박의 속력이 모두 동일하며 감속, 가속이 불가능한 상황에서 실험을 진행하였다. 그러나 선속의 감속 및 모든 선박의 속력을 다르게 하여 실험할 필요가 있다.