DBSCAN을 이용한 등부표 위치 데이터 Clustering 연구(Ⅰ)
A Study on Data Clustering of Light Buoy Using DBSCAN(Ⅰ)
Article information
Abstract
등부표는 조류, 바람 등 외력에 영향을 받아 위치가 항상 유동적이고 위치는 항로표지용 AIS 또는 RTU를 통해 확인할 수 있다. 위치 확인이 가능한 등부표의 최근 5년간(2017~2021년) 위치 데이터 분석 결과 위치 오류 데이터는 평균 15.4%로 나타났으며 항해 안전사고예방 및 관리를 위해서는 위치 오류 데이터를 검출하고 정제된 위치 데이터 획득이 필요하다. 본 연구에서는 항로표지용 AIS 또는 RTU를 통해 획득한 위치 데이터를 DBSCAN Clustering하여 위치 오류 데이터를 검출하고 정제된 위치 데이터를 획득하고자 한다. 이를 위하여 위치 오류가 가장 많은 서해 해역 중 RTU가 설치된 군산항 1호 등부표의 21년도 위치 데이터를 Python library를 사용하여 DBSCAN Clustering 하였다. DBSCAN Clustering에 필요한 minPts는 2차원 데이터에 일반적으로 사용하는 값을 적용하였고 epsilon은 k-NN(최근접이웃)알고리즘을 사용하여 값을 산출 및 적용하였다. DBSCAN Clustering 결과 minPts와 epsilon을 만족하지 못하는 위치 오류 데이터를 검출하였고 정제된 위치 데이터를 획득할 수 있었다. 본 연구는 항로표지용 AIS 또는 RTU가 설치된 등부표의 신뢰성 있는 위치 데이터를 획득할 수 있는 기초 자료로 활용할 수 있으며 항해 안전사고 예방에도 큰 도움이 될 것으로 판단된다.
Trans Abstract
The position of a light buoy is always flexible due to the influence of external forces such as tides and wind. The position can be checked through AIS (Automatic Identification System) or RTU (Remote Terminal Unit) for AtoN. As a result of analyzing the position data for the last five years (2017-2021) of a light buoy, the average position error was 15.4%. It is necessary to detect position error data and obtain refined position data to prevent navigation safety accidents and management. This study aimed to detect position error data and obtain refined position data by DBSCAN Clustering position data obtained through AIS or RTU for AtoN. For this purpose, 21 position data of Gunsan Port No. 1 light buoy where RTU was installed among western waters with the most position errors were DBSCAN clustered using Python library. The minPts required for DBSCAN Clustering applied the value commonly used for two-dimensional data. Epsilon was calculated and its value was applied using the k-NN (nearest neighbor) algorithm. As a result of DBSCAN Clustering, position error data that did not satisfy minPts and epsilon were detected and refined position data were acquired. This study can be used as asic data for obtaining reliable position data of a light buoy installed with AIS or RTU for AtoN. It is expected to be of great help in preventing navigation safety accidents.
1. 서 론
오늘날 해상 및 육상에는 통항 선박의 해양사고 예방을 위해 다양한 종류의 항로표지를 설치하여 운영하고 있다.
항로표지는 해상교통의 안전을 도모하고 선박의 능률성을 향상시키는데 기여하는 해상교통안전 시설로서 관련 법령에 따라 광파, 형상, 전파, 음파, 특수신호표지로 구분된다. 그중 등부표는 선박 통항의 안전을 위해서 필요한 시설로, 항해하는 선박에게 암초나 수심이 얕은 곳의 소재를 알리거나 또는 항로의 경계를 알리기 위하여 해상의 고정 위치에 띄워놓은 구조물을 말한다(Jeong and Gug, 2013).
해상에 설치되어 운영중인 등부표는 광파표지의 한 종류로 방파제등대 다음으로 많이 설치되어 있다.
등부표는 해저에 계류된 침추, 체인을 이용하여 해면상에 뜨게 한 구조물로서 바람, 조류, 파고 등 외력에 항상 영향을 받는다. 따라서 등부표는 이출 범위 내에서 외력에 의해 표류하기 때문에 위치가 수시로 변하게 되고, 외력이 심할 경우에는 최대 이출 위치를 벗어나는 경우(항로표지 사고)가 발생하기도 한다(KIM, et al, 2020).
이를 보완하고 효율적으로 등부표를 관리를 위해 해양수산부에서는 2006년부터 항로표지 집약관리시스템을 전국 해역을 13개 권역으로 구분하여 운영 중에 있다(MOF, 2006).
항로표지 집약관리 시스템은 무인으로 운영되는 항로표지의 기능 상태를 감시 및 제어할 수 있도록 구성되어 있는 시스템을 말하며 항로표지용 AIS 또는 RTU 장비를 부착해서 다양한 형태의 메시지를 통해 원격으로 등부표의 위치 및 상태를 확인할 수 있다.
등부표에서 전송되는 위치 데이터는 장비 오차와 해상상태의 영향으로 인해 많은 오류가 발생할 수 있다. 하지만 지금까지 항로표지용 AIS 또는 RTU와 관련된 연구는 주로 통신 횟수, 통신 상태 등에 대한 연구가 이루어졌다.
따라서 등부표에서 전송되는 위치 데이터는 장비에서 발생하는 오차와 해상상태 등에 영향을 받아 오류가 발생할 수 있으므로 등부표에서 송신하는 위치 데이터의 정확성과 오류를 확인할 필요가 제기되었다(Gug, et al, 2013; Jun, et al, 2011).
또한, 최근 5년간(2017∼2021년) 등부표 위치데이터 분석 결과 위치 오류가 전체 평균 15.4%로 나타났으며 항로표지를 관리하는 관리자 입장에서 신뢰할 수 있는 정확한 위치 데이터를 확보하기 위한 방법이 필요함을 제기하였다(Moon, et al, 2022).
이와같이 항로표지용 AIS 또는 RTU가 설치된 등부표 관련하여 통신 횟수, 통신 상태, 위치 데이터 분석 등 여러 선행연구가 진행되었지만 발생하는 위치 오류를 검출하고 신뢰할 수 있는 위치 데이터를 획득하는 방안에 대한 연구는 미흡한 것으로 판단된다.
본 연구의 목적은 항로표지용 AIS 또는 RTU가 설치된 등부표 위치 데이터에 대해 DBSCAN(Density-Based Spartial Clustering of applications with noise, 밀도 기반 군집화)이용 Clustering을 통해 위치 오류 데이터를 검출하고 정제된 데이터를 획득하여 관리자와 사용자에게 신뢰성 있는 위치 데이터를 제공함으로써 효율적인 등부표 관리와 항해 안전사고 예방에도 도움을 주고 또한, 위치 데이터의 품질 향상을 위한 기초 자료로도 활용할 수 있도록 하는데 있다.
본 연구에서는 위치 오류가 가장 많이 발생하는 해역을 고려하여 군산항 1호 등부표를 선정하였고 Python library를 사용하여 21년도 위치 데이터를 DBSCAN Clustering 하였다.
2. 등부표 현황 및 관리 시스템
우리나라 전 해역 해상에서 운영 중인 등부표는 방파제등대 다음으로 많이 설치되어 운영 중이고 그중 항로표지용 AIS 또는 RTU 가 설치되어 운영 중인 국유 등부표(Spar buoy 제외)는 Table 1에서와 같이 AIS가 설치된 등부표는 48기, RTU가 설치된 등부표는 189기로 총 237기를 운영하고 있다(MOF, 2022).
등부표 위치는 침추가 정치(定置)된 위치를 말하며, 침추와 표체가 체인으로 연결되어 이출 거리가 발생하는 부유식(이하 등부표)과 침추와 표체가 바로 연결되어 이출 거리가 발생하지 않는 고정식 부표(Spar buoy)로 구분할 수 있다.
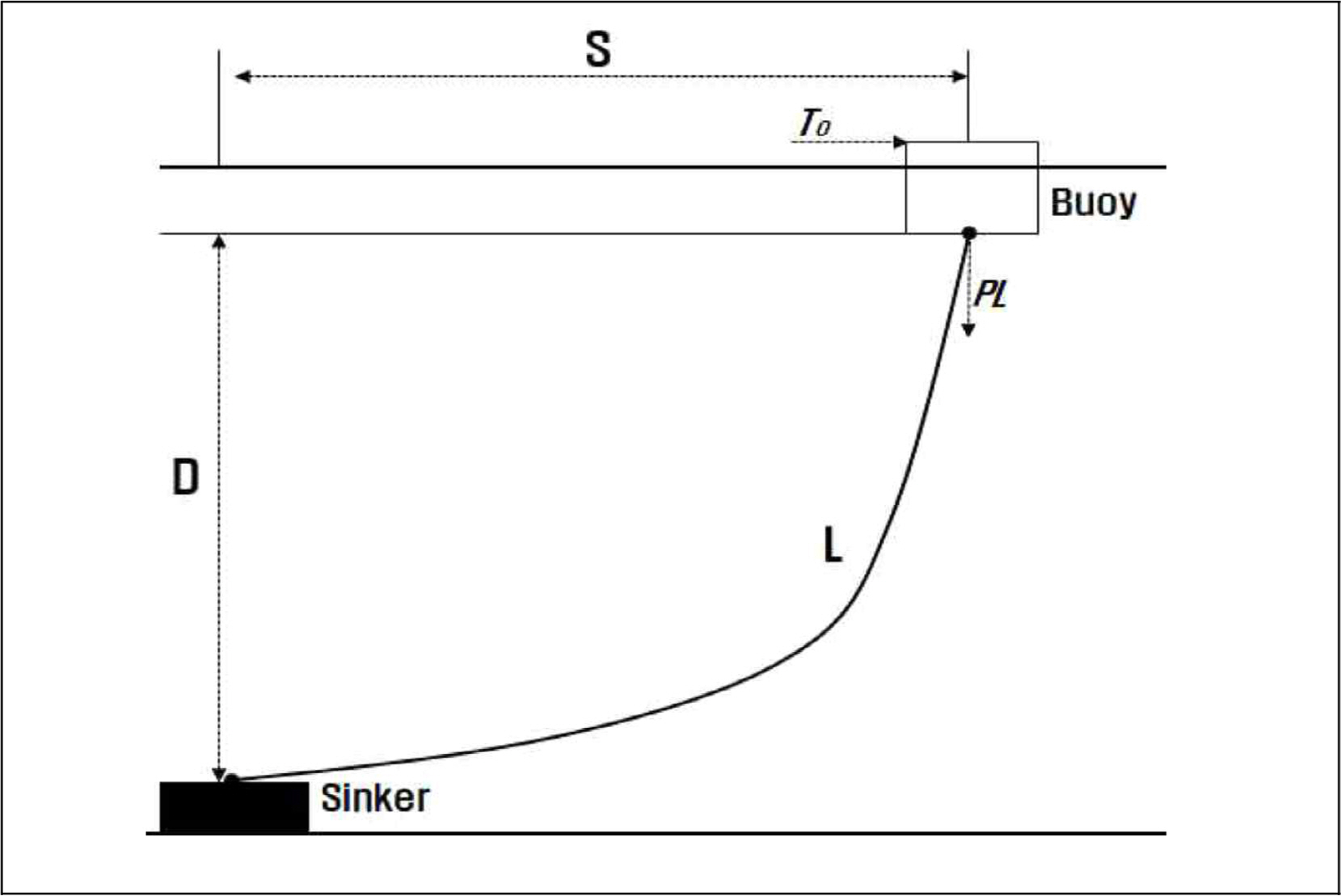
Fig. 1은 등부표의 이출거리 개념도로서 등부표의 표체(Buoy)는 침추(Sinker)와 체인으로 연결되어 외력(조류, 바람 등)에 의해 이출거리(S)가 발생하기 때문에 침추(Sinker)를 중심으로 선회반경이 만들어진다. 이와같은 외력에 의해 발생하는 등부표의 선회반경 크기는 체인길이(L)에 따라 다르며 체인길이는 등부표의 종류, 설치 수심(D), 체인의 수중중량, 외력 등을 고려하여 결정된다(MOF, 2014).
등부표의 이출거리는 설치되는 지점에 따라 외력(바람, 조류, 파고 등), 수심 등 이출거리에 영향을 미치는 요인들이 다르기 때문에 같은 형식의 등부표일지라도 이출거리가 상이할 수 있다.
등부표의 이출거리는 침추를 중심으로 이격되어 있는 등부표의 이출위치로 등부표에 부착된 항로표지용 AIS 또는 RTU를 통해 송신되는 위치데이터를 이용하여 확인 가능하며 식(1) 또는 근사식으로 식(2)와 같이 계산한다(Jeong and Gug, 2013).
여기서, T0 : 침추 지점에서 체인의 수평방향 장력성분
P : 체인의 수평장력
L : 체인의 길이
D : 계산기준 수심
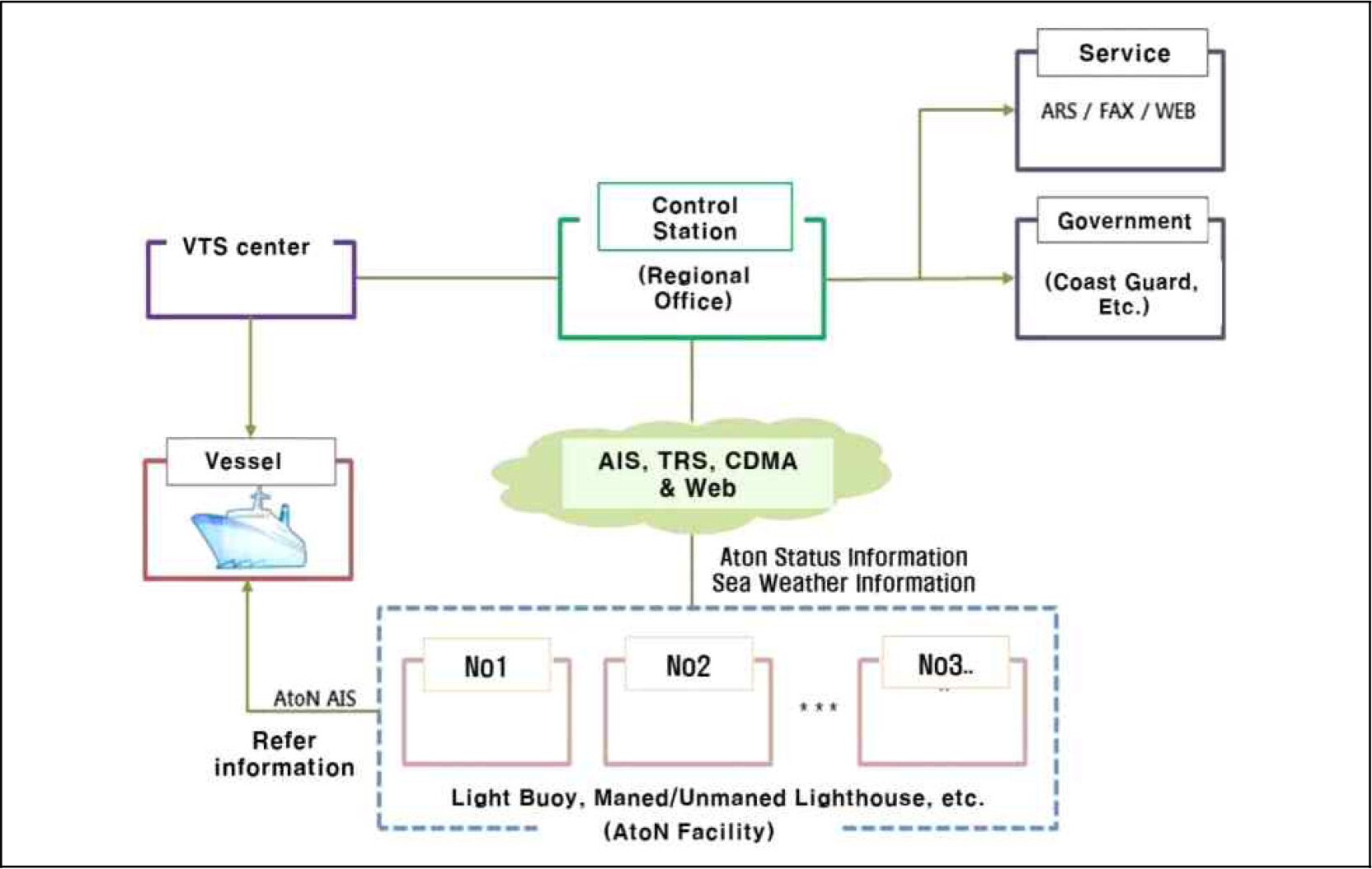
Fig. 2는 항로표지 집약관리시스템을 나타내는 것으로 항로표지용 AIS 또는 RTU 가 설치된 항로표지의 상태정보를 24시간 원격으로 감시 및 정보수집할 수 있도록 자국과 모국으로 시스템이 구성되어 있다.
자국은 등대, 등부표, 등표와 같은 독립된 항로표지이며, 모국은 지방청(항로표지 관리운영시스템)이다. 항로표지의 원격감시 및 정보 수집은 항로표지에 부착된 항로표지용 AIS와 RTU 장비를 통해서 가능하며 통신방식은 항로표지용 AIS는 AIS 통신망을 사용하고 RTU는 CDMA, TRS 등 다양한 방식을 사용한다.
항로표지용 AIS가 설치된 항로표지는 항로표지 상태정보(메시지 8번 및 21번)를 이용자에게 직접 제공 하거나 국립해양측위정보원으로 전송하여 저장 관리하고 항로표지용 RTU가 설치된 항로표지의 상태정보는 직접 모국(지방청)으로 전송되어 저장되고 이후 국립해양측위정보원으로 전송된다(MOF, 2015).
항로표지용 AIS 또는 RTU가 설치된 등부표 위치 데이터의 최근 5년간(2017~2021년) 위치오류 분석 결과를 보면 전체 평균은 15.4%로 나타났으며 해역별로는 동해가 2.6%로 가장 낮았고, 남해가 14.0%, 서해가 27.3%로 가장 높았다. 장비별로는 AIS가 19.5%, RTU가 12.8%의 위치 오류가 발생하여 정확한 위치 데이터 확보 방법이 필요함이 제기되었다(Moon, et al, 2022).
따라서, 관리자의 효율적인 등부표 관리와 해양 안전사고 예방을 위해서는 위치 오류 데이터를 검출하고 신뢰할 수 있는 정제된 위치 데이터를 획득하는 것이 무엇보다 중요하다고 판단된다.
3. DBSCAN Clustering 방법 및 절차
DBSCAN(Density-based spatial clustering of application with noise)은 머신러닝 비지도 학습 중 하나로 데이터의 밀도를 기준으로 Cluster(군집)를 확장해 나가는 Clustering algorithm으로, 초기 데이터로부터 군집한 데이터를 찾아가는 방법으로 군집을 확장한다(M. Ester, et al, 1996).
DBSCAN 알고리즘은 k-means 알고리즘과 함께 군집분석에서 가장 많이 활용되고 있으며 DBSCAN 알고리즘은k-means 알고리즘에 비해 군집의 개수(k)를 미리 정할 필요가 없고 군집의 모양과 사이즈가 다양하게 나올 수 있는 알고리즘이다.
특히, DBSCAN 알고리즘은 거리 기반의 k-means 알고리즘과 달리 밀도 기반의 군집 방법이므로 위치 데이터를 분석하는데 탁월한 효과를 가지고 있어 선박의 최적항로 생성 기술에도 활용하고 있다(Wen, et al, 2020).
DBSCAN 알고리즘을 사용하기 위해서는 ε(Epsilon)과 minPts(Minimum Points) 두 가지 정보가 필요하다.
ε는 각 데이터들이 서로에게 이웃인지 판단하기 위한 최소거리이며, minPts는 Cluster로 인정하기 위한 ε내의 최소 데이터 개수이다.
ε는 각 데이터들이 서로에게 이웃인지 판단하기 위한 최소거리로 k-NN(k-Nearest Neighbor, k-최근접 이웃) 알고리즘을 적용하여 k 거리에 대한 분포 그래프를 이용하여 최적의 ε값을 추정할 수 있다(Beyer, et al, 1999).
k-NN(k-Nearest Neighbor) 알고리즘은 머신러닝 지도 학습 알고리즘의 한 종류로서 분류(classification)와 회귀(regression) 예측 문제에서도 사용되나 주로 분류 알고리즘으로 사용되며 새로운 데이터에 대해 기존 데이터 중 가장 가까운 k 개 이웃 데이터의 정보를 통해 새로운 데이터의 정보를 예측하는 방법론을 의미한다(Onel Harrison, 2018).
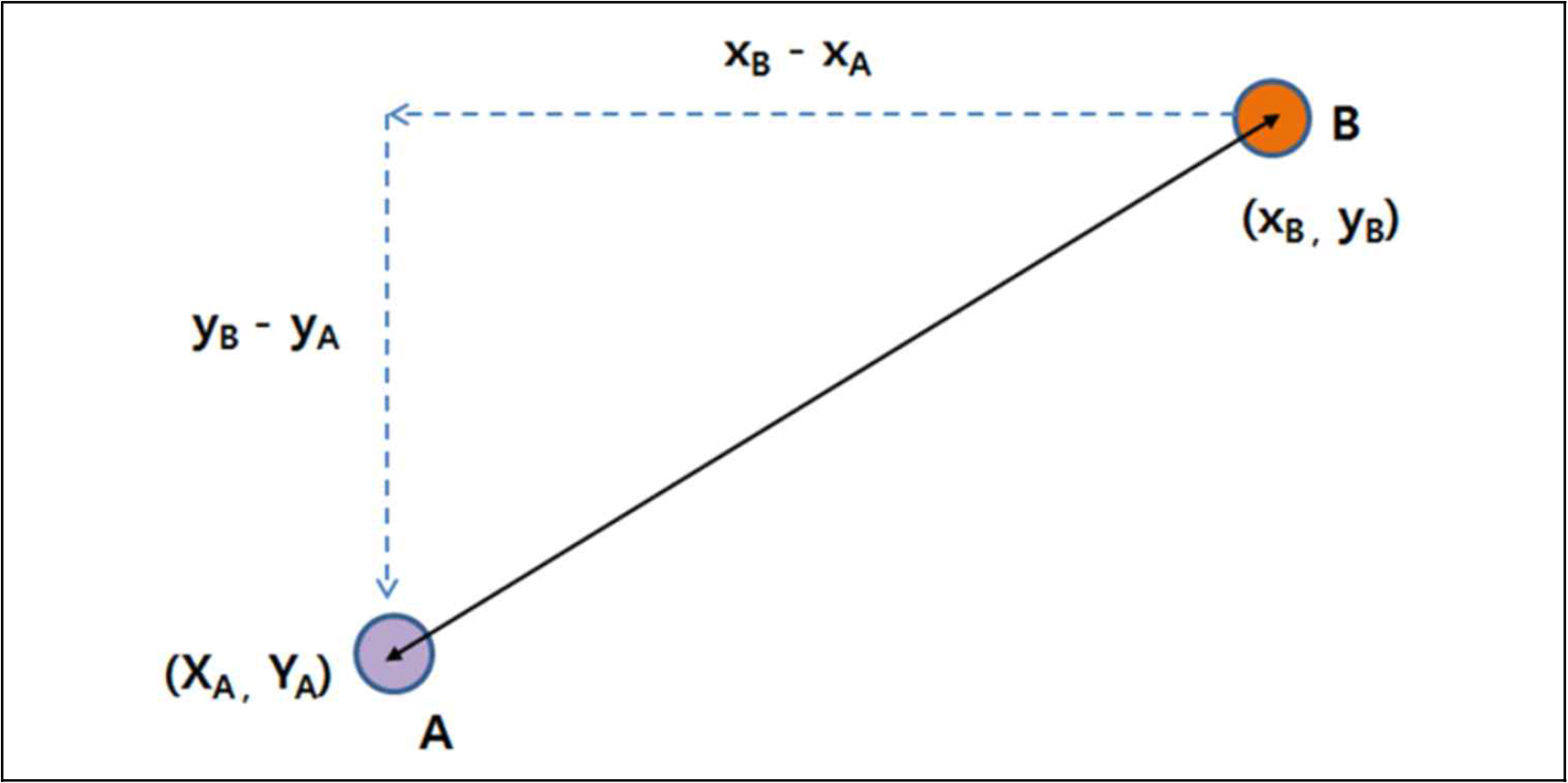
k-NN에서 ε 값을 구하기 위한 데이터 간 거리 측정 방법은 Fig. 3과 같은 유클리디안 거리(Eucledian Distance) 측정 방법을 할용하며 계산식은 식(3)과 같다(Choi, et al, 2021).
minPts는 Cluster로 인정하기 위한 ε내의 최소 데이터 개수로 만약 minPts가 너무 작은 수이면 잡음(Noise)으로 구분되어야 할 데이터들도 Cluster로 형성될 수 있으므로 minPts 설정에 주의가 필요하다.
일반적으로 minPts는 데이터 셋트의 차원보다 크거나 같아야 하고 2차원의 데이터의 경우 minPts는 4를 사용할 것을 권장하고 있다(M. Ester, et al, 1996).
Fig. 4는 minPts가 4일 경우 Clustering 절차를 보여주는 것으로 ε내에 minPts 이상의 데이터가 있다면 Cluster를 생성하고 이웃데이터를 중심으로 동일한 검사를 하여 Cluster를 확장해 나간다. 만약 ε내에 minPts 미만의 데이터가 있으며, 그 데이터들의 이웃 데이터 수가 minPts보다 적다면 이 데이터들을 Noise로 정의한다(Lee, et al, 2017)
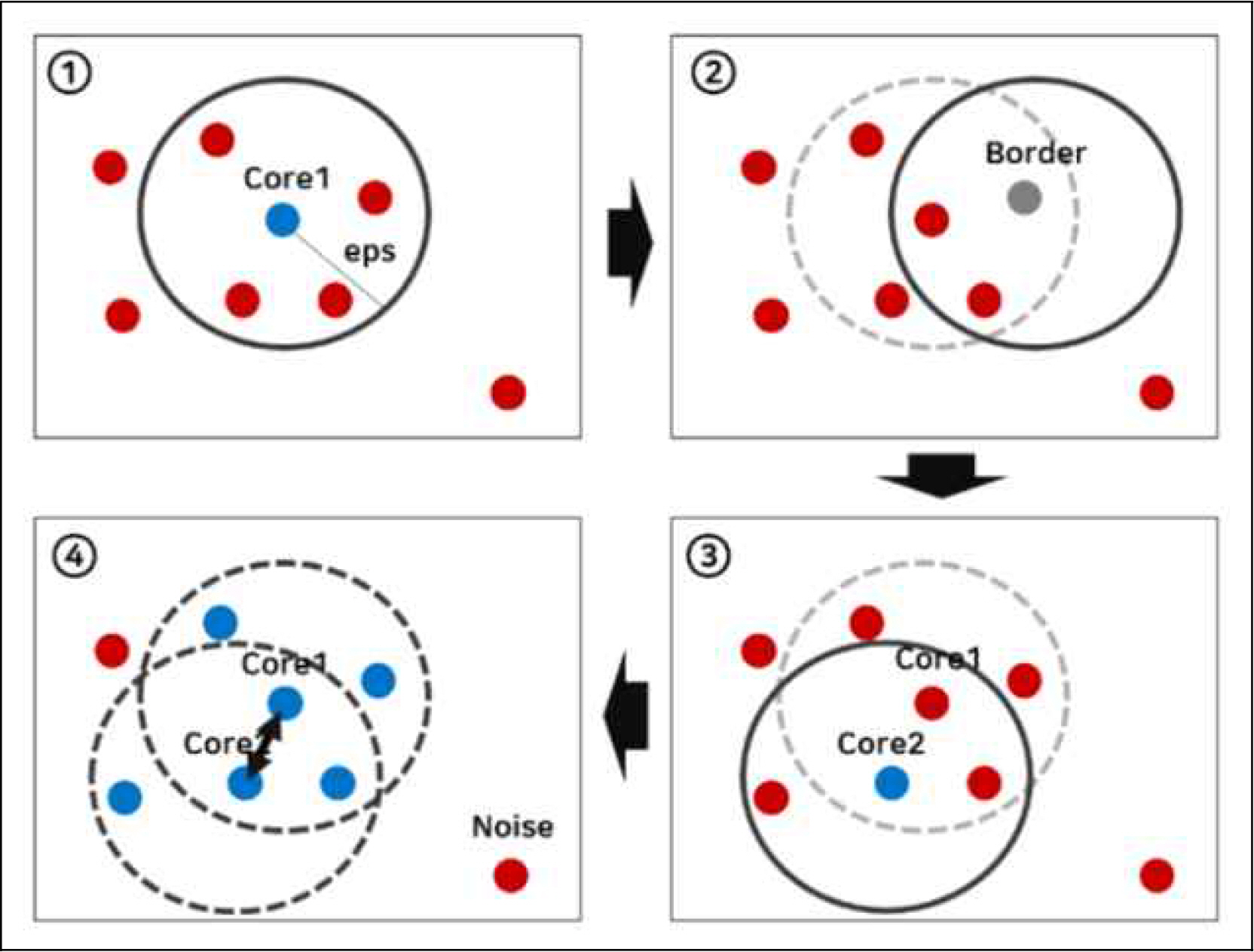
Process for creating clusters with DBSCAN
Source : https://blog.naver.com
DBSCAN을 이용하여 등부표 위치 데이터에서 Noise(오류 데이터)를 검출하고 정제된 위치 데이터를 획득하기 위해서는 등부표가 설치된 고시 위치와 수신 위치 간의 거리를 구한 뒤 위치 데이터에 대해 기초분석을 해야 한다. 수신 위치는 등부표가 고시위치로부터 이격되어 있는 위치로 고시위치와 수신위치 거리는 식(4)를 사용하여 산출 하였다(NGII, 2022).
여기서, X1 : 고시좌표 위도
X2 : 수신위치 위도
Y1 : 고시좌표 경도
Y2 : 수신위치 경도
Fig. 5는 등부표 위치 데이터를 DBSCAN Clustering 하여 Noise를 검출하는 절차를 나타낸 것으로 우선 수신한 등부표 위도와 경도 위치를 식(4)를 사용하여 고시 위치와 수신 위치 간의 거리를 구한 뒤 전체 위치 데이터의 분포도, 체인 이출거리 이내 위치 데이터 선별 등 기초 분석한다.
DBSCAN 알고리즘 사용에 필요한 ε 값은 k-NN알고리즘을 사용하여 전체 위치 데이터와 체인 이출거리 이내 위치 데이터에서 각각 산출하고 minPts는 4로 설정한다.
산출한 ε와 minPts 4를 적용하여 전체 수신 위치 데이터에 대해 1차 DBSCAN Clustering 하여 ε와 minPts를 만족하지 못하는 Noise(오류 데이터)를 1차 검출하고, 체인 이출거리 이내 데이터에 대해 2차 DBSCAN Clustering하여 ε와 minPts를 만족하지 못하는 Noise(오류 데이터)를 2차 검출함으로써 정제된 위치 데이터를 획득할 수 있다.
4. DBSCAN Clustering 분석 및 평가
본 연구에서는 항로표지용 AIS 또는 RTU가 설치되어 있는 등부표(237/Spar buoy 제외) 중에서 위치오류가 가장 많이 발생하는 해역을 고려하여 RTU가 설치된 군산항 1호 등부표를 선정하였고 21년도(‘21. 1. 1.-12.31.) 위치 데이터에 대해 Python Library를 이용하여 DBSCAN Clustering을 시행하였다.
Table 2는 군산지방해양수산청과 항로표지 전산 관리시스템을 통해 획득한 군산항 1호 등부표의 설치 제원 및 정보 사항과 21년도 위치 데이터에 대해 기초 분석한 것으로 등부표 종류는 LL-26(M)이며 설치 수심은 13.8m, 체인 길이는 35m, 데이터 수신 간격은 10분이며 수신 데이터는 49,640개이다.
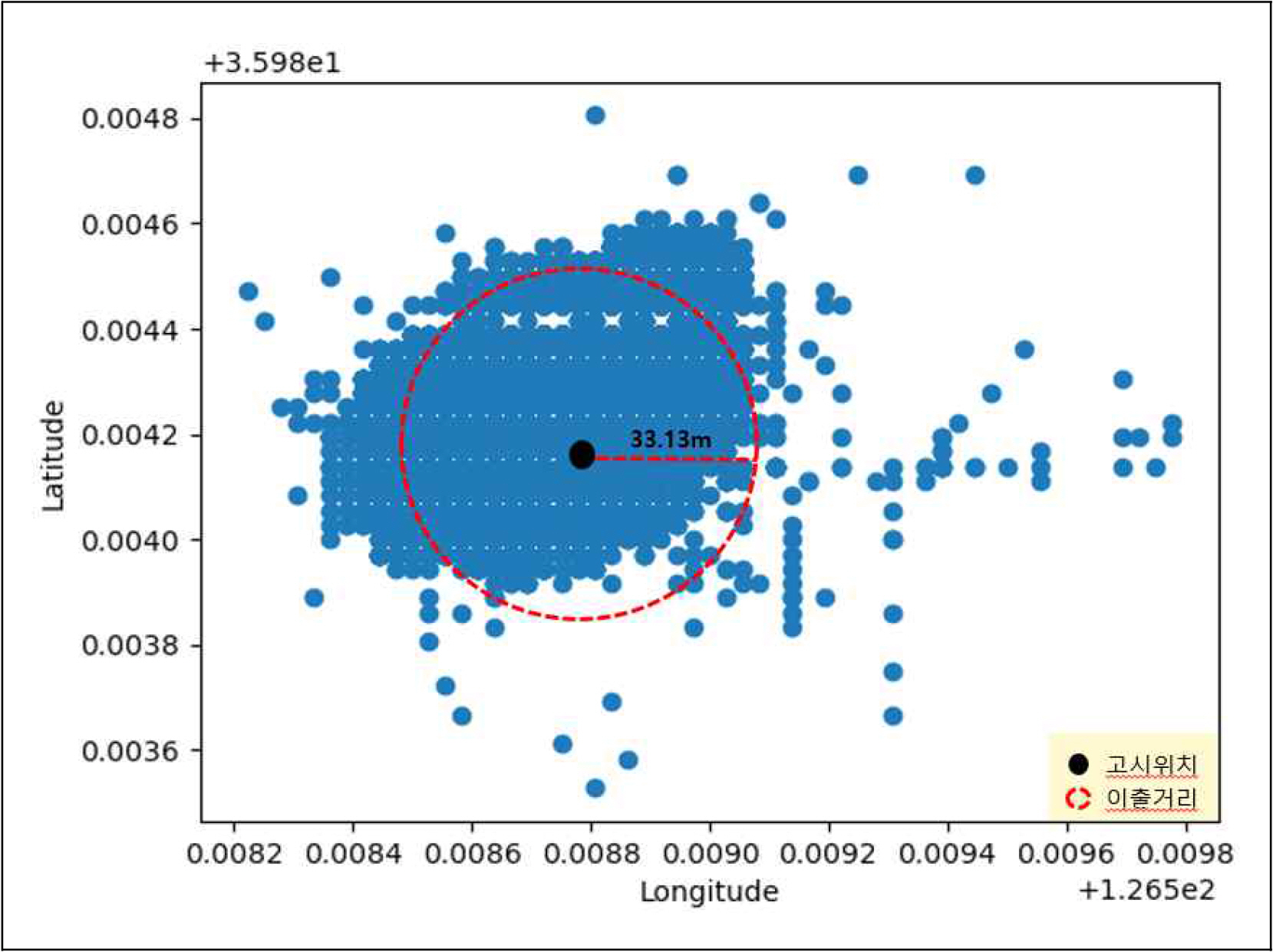
수신 데이터(49,640개)에 대한 고시위치와 등부표의 거리는 식(4)를 사용하여 산출하였고 체인 이출거리는 식(1)을 사용하여 산출하였으며 체인 이출거리는 33.13m로 산출되었다.
수신 데이터(49,640개) 중 체인 이출거리 이내 신뢰성 있는 유효 데이터는 44,370개로 수신 데이터 대비 유효 데이터는 89.4%, 체인 이출거리를 초과한 데이터는 5,270개로 10.6%를 차지하였다.
Fig. 6은 고시 위치와 수신 위치 간의 거리에 따른 데이터 분포도로서 수신 데이터(49,640개)에 대해 식(4)를 사용하여 산출한 고시 위치와 수신 위치 간의 거리에 따른 위치 데이터 분포를 보여주고 있으며 식(1)을 사용하여 산출한 체인 이출거리(33.13m)와 비교시 체인 이출거리를 초과한 위치 데이터는 5,270개로 최대 92.7m까지 초과 되었다.
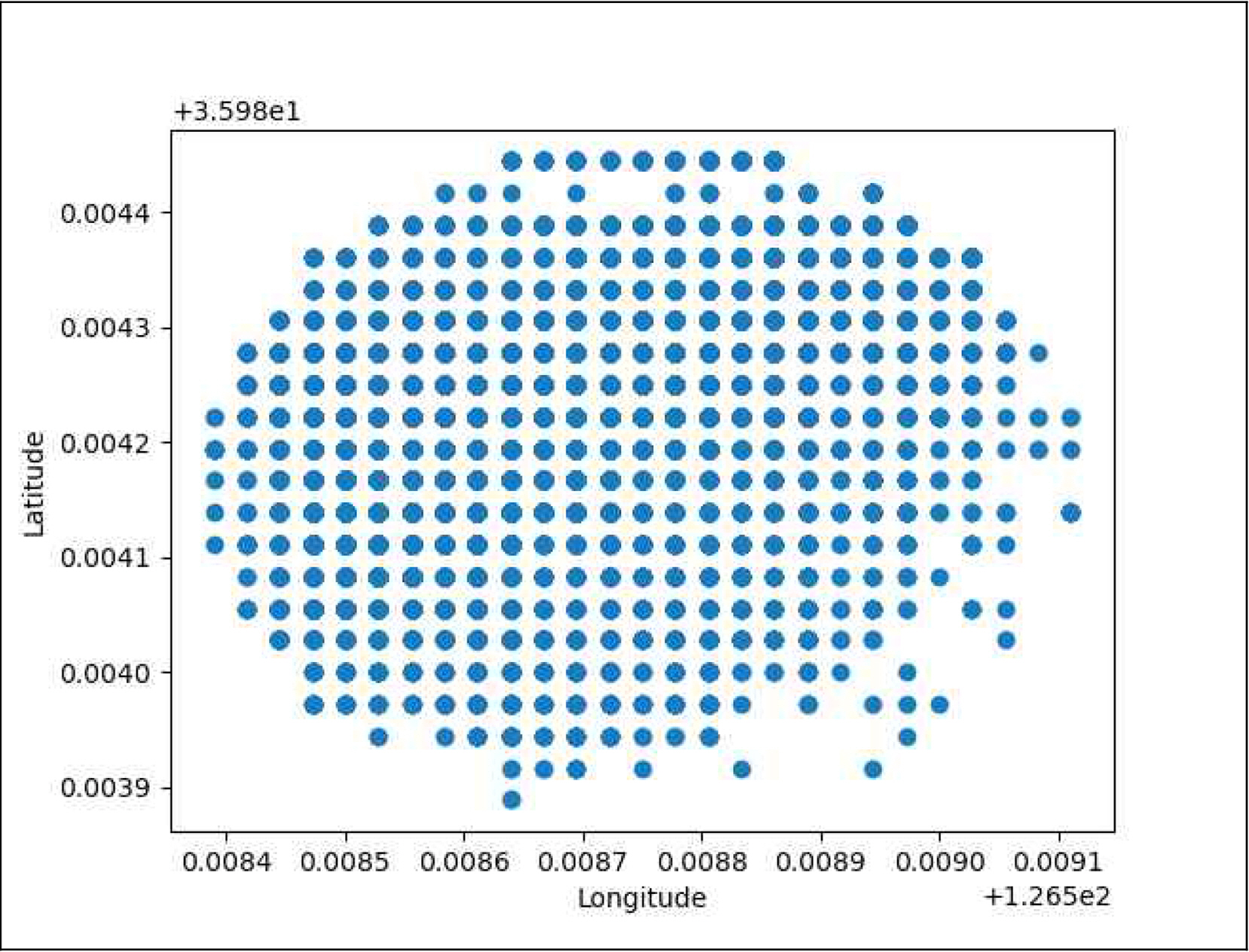
Fig. 7은 수신 위치 데이터(49,640개)의 산점도(Scatter plot)를 보여주고 있는 것으로 기초 분석을 바탕으로 수신 데이터의 위치분포를 확인해 보았으며 분포 형태는 체인의 길이에 따라 형성되는 원형이 아닌 타원형의 형태로서 군산항 1호 등부표는 항내에 위치하고 있고 조차가 큰 서해안의 특성을 고려 했을 때 바람이나 파도보다는 조류 방향에 따라 고시 위치(침추)를 중심으로 타원형으로 형성된 것으로 판단된다.
또한, Fig. 6의 데이터 분포도에서 나타난 것과 같이 체인 이출거리(33.13m)를 초과한 데이터가 많이 식별됨을 알 수 있으며 기간 중 등부표의 위치 이동이나 교체가 없었기 때문에 통신오류 또는 위치오류로 추정할 수 있다.
다음으로 수신 위치 데이터(49,640개)에 대한 DBSCAN Clustering을 통해 Noise를 검출하기 위해서는 ε와 minPts 설정이 중요하다.
ε는 각 데이터들이 서로에게 이웃인지 판단하기 위한 최소거리로 k-NN(k-Nearest Neighbor, k-최근접 이웃) 알고리즘을 적용하여 k 거리에 대한 분포 그래프를 이용하여 최적의 ε 값을 산출하였다.
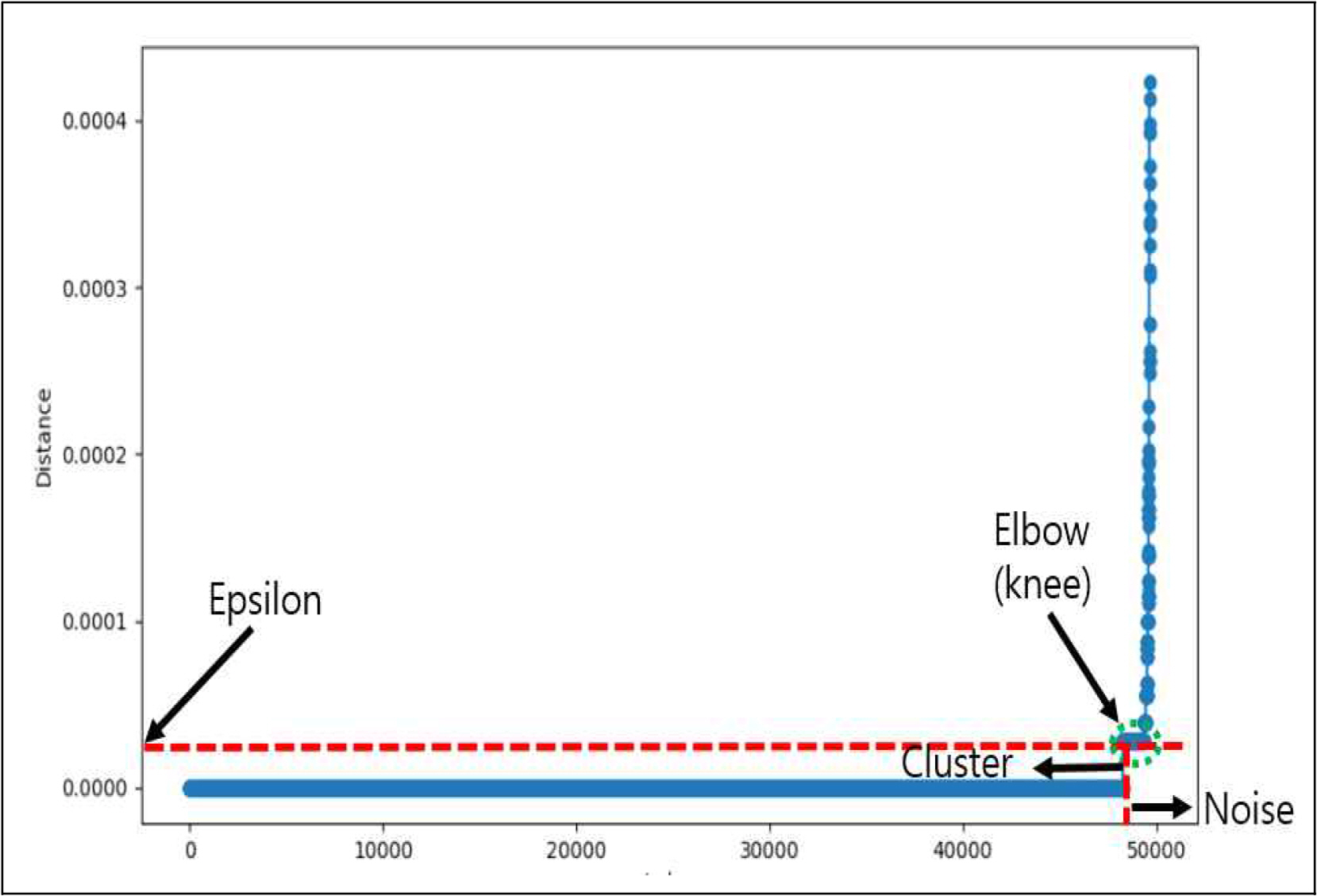
Fig. 8은 ε 값을 산출하기 위해 k-NN 알고리즘을 이용하여 작성한 이웃거리 그래프를 나타내고 있으며 거리가 급격히 변하는 Elbow(Knee) point가 최적의 ε로서 k 값 1을 적용하여 산출한 수신한 전체 위치 데이터의 ε는 0.000306으로 산출되었다.
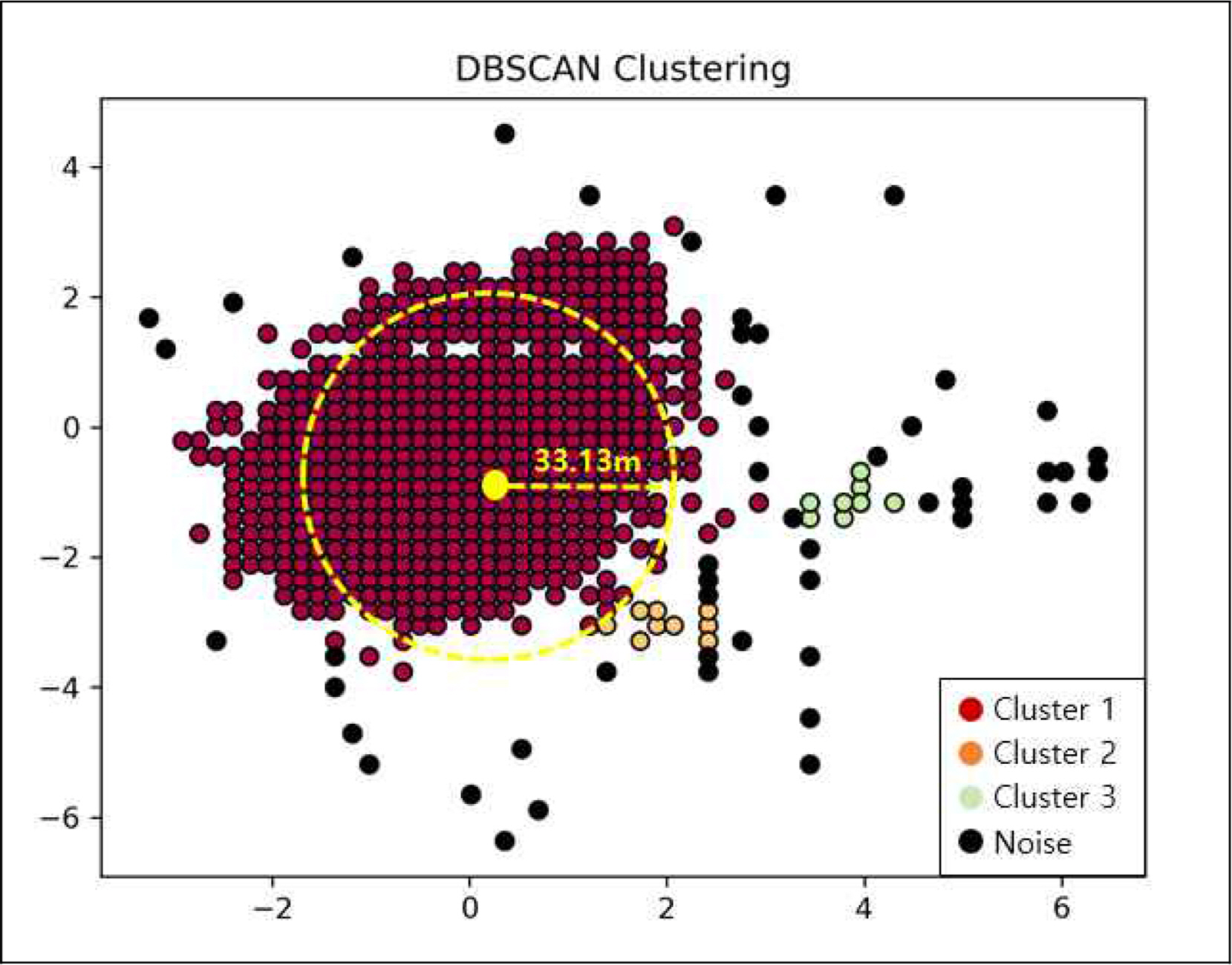
Fig. 9는 k-NN 알고리즘 이용 산출한 ε(0.000306)와 2차원 데이터에서 일반적으로 사용하는 minPts(4)를 적용하여 수신한 전체 위치 데이터에 대한 1차 DBSCAN Clustering 결과를 보여주고 있는 것으로 이출거리 이내의 위치 데이터에서는 1개의 Cluster( )가 형성되었고 이출거리를 초과한 위치 데이터에서는 3개의 Cluster(
)가 형성되었고 이출거리를 초과한 위치 데이터에서는 3개의 Cluster( )가 형성되었으며 ε와 minPts를 만족하지 못하는 검정색 point가 Noise이다.
)가 형성되었으며 ε와 minPts를 만족하지 못하는 검정색 point가 Noise이다.
체인 이출거리를 초과한 위치 데이터에서도 Cluster가 형성되었고 Noise는 체인 이출거리 이내 위치 데이터에서는 발생하지 않았으며 체인 이출거리를 초과한 위치 데이터에서 많이 발생하였다.
수신 위치 데이터(49,640개)에 대한 DBSCAN Clustering 결과 체인 이출거리를 초과한 위치 데이터에서도 Noise로 처리되지 않고 Cluster로 형성되어 관리자와 사용자에게 제공되는 위치 데이터에 대한 신뢰도가 낮다고 볼 수 있다.
따라서, 관리자와 이용자에게 신뢰성 있는 위치 데이터를 제공하기 위해 이출거리 이내 위치 데이터(44,370개)를 이용하여 동일한 절차와 방법으로 2차 DBSCAN Clustering을 수행하였다.
Fig. 10은 2차 DBSCAN Clustering에 사용할 이출거리 이내 데이터의 산점도(Scatter plot)를 나타내고 있으며 분포 형태는 타원형의 형태로서 조차가 큰 서해안의 특성을 고려 했을 때 조류 방향에 따라 고시 위치(침추)를 중심으로 타원형으로 형성된 것으로 판단되고 일부 구역에서 밀집도가 낮은 데이터가 발생하였다.
ε 값은 1차와 동일하게 k-NN 알고리즘을 이용하여 0.000028로 산출 되었고 minPts는 1차 DBSCAN Clustering과 동일하게 4를 적용하였다.
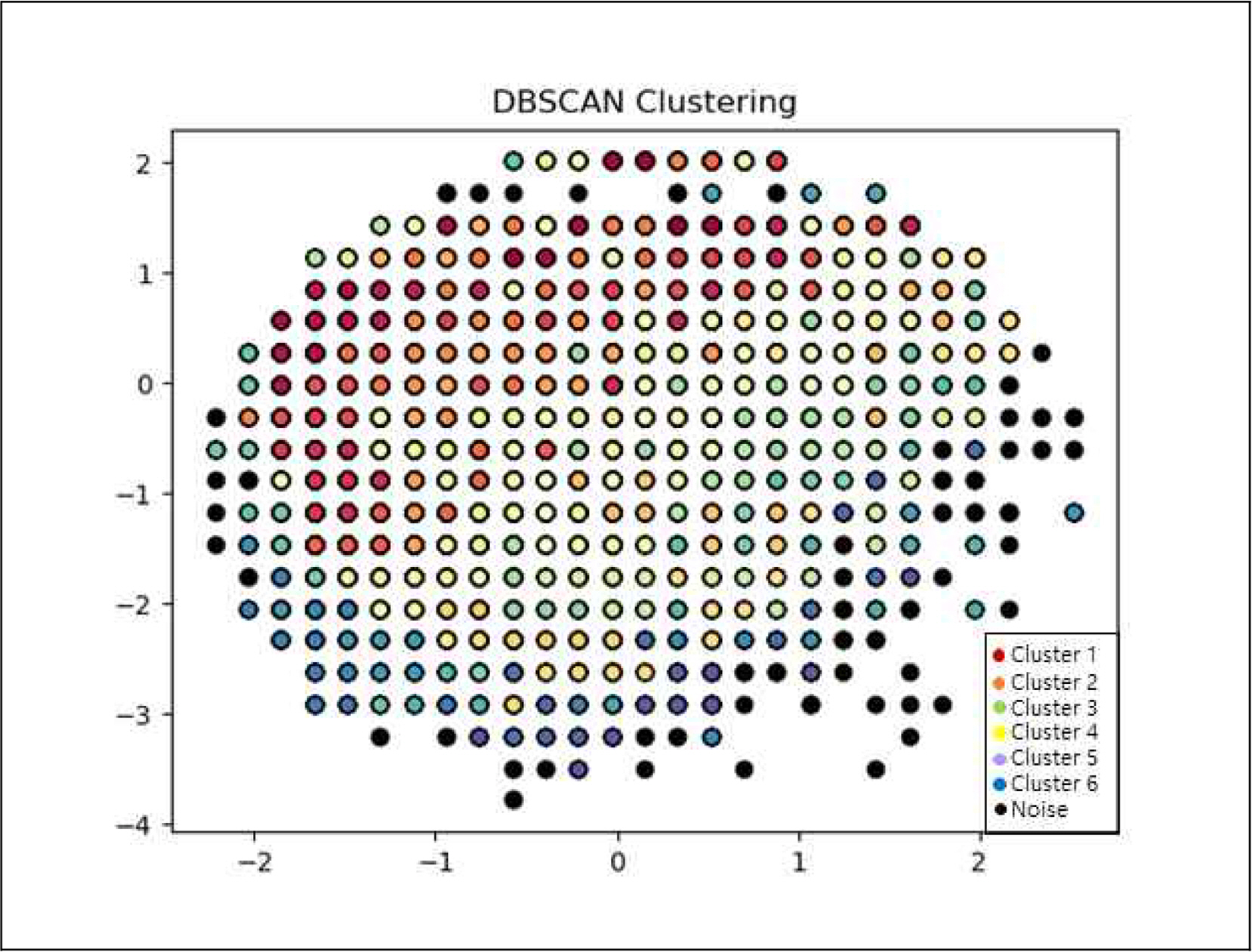
Fig. 11은 k-NN 알고리즘 이용 산출한 ε 값 0.000028과 minPts 4를 적용하여 이출거리 이내 위치 데이터에 대한 DBSCAN Clustering 결과를 보여주고 있으며 여러 가지 형태의 Cluster( )가 형성되었고 ε와 minPts를 만족하지 못하는 검정색 point가 Noise로 신뢰성 있는 이출거리 이내 위치 데이터에서도 Noise가 검출됨을 알 수 있으며 검출된 Noise는 Fig. 10의 이출거리 이내 위치 데이터의 산점도(Scatter plot)에서 나타난 것과 같이 밀집도가 낮은 부분에서 검출되었으며 통신 오류나 위치 오류로 추정된다.
)가 형성되었고 ε와 minPts를 만족하지 못하는 검정색 point가 Noise로 신뢰성 있는 이출거리 이내 위치 데이터에서도 Noise가 검출됨을 알 수 있으며 검출된 Noise는 Fig. 10의 이출거리 이내 위치 데이터의 산점도(Scatter plot)에서 나타난 것과 같이 밀집도가 낮은 부분에서 검출되었으며 통신 오류나 위치 오류로 추정된다.
Fig. 12는 2차 DBSCAN Clustering에서 검출한 Noise 데이터만을 나타내고 있는 것으로 여러 과정과 절차를 통해 Noise를 검출하고 정제된 위치 데이터를 획득할 수 있었다.
이와 같이 획득한 정제된 위치 데이터를 관리자 및 사용자에게 제공함으로써 위치 데이터에 대한 신뢰성 향상과 효율적인 등부표 관리 및 항해 안전사고 예방에도 도움이 될 것으로 판단된다.
5. 결 론
본 연구는 항로표지용 AIS 또는 RTU가 설치된 등부표 수신 위치 데이터에 대한 DBSCAN Clustering을 통해 오류 데이터(Noise)를 검출하고 정제된 데이터를 획득하는 방안에 대한 기초 연구로서 군산항 1호등부표(LL-26(M))의 21년도 위치 데이터(49,640개)를 사용하여 DBSCAN Clustering하였다.
DBSCAN Clustering을 하기 위해 필요한 ε(Epsilon) 값은 k-NN 알고리즘을 이용 산출하였고 minPts(Minimum Points)는 2차원 데이터에서 일반적으로 사용하는 4를 적용하였다.
ε와 minPts를 적용하여 수신한 전체 위치 데이터와 이출거리 이내 위치 데이터에 대한 1차, 2차 DBSCAN Clustering한 결과 ε와 minPts를 만족하지 못하는 Noise를 검출하였고 정제된 위치 데이터를 획득할 수 있었다.
수신한 전체 위치 데이터(49,640개)에 대한 1차 DBSCAN Clustering에서는 이출거리 이내(33.13m)의 위치 데이터에서 1개의 Cluster( )와 이출거리를 초과한 위치 데이터에서도 Noise로 처리되지 않고 3개의 Cluster(
)와 이출거리를 초과한 위치 데이터에서도 Noise로 처리되지 않고 3개의 Cluster( )가 형성되어 관리자와 사용자에게 제공되는 위치 데이터에 대한 신뢰도가 낮다고 볼 수 있으며 ε와 minPts를 만족하지 못하는 Noise는 이출거리를 초과한 위치 데이터에서 검출되었으며 기간 중 등부표의 위치 이동이나 교체가 없었기 때문에 통신오류 또는 위치오류로 추정할 수 있다.
)가 형성되어 관리자와 사용자에게 제공되는 위치 데이터에 대한 신뢰도가 낮다고 볼 수 있으며 ε와 minPts를 만족하지 못하는 Noise는 이출거리를 초과한 위치 데이터에서 검출되었으며 기간 중 등부표의 위치 이동이나 교체가 없었기 때문에 통신오류 또는 위치오류로 추정할 수 있다.
신뢰성이 있는 이출거리 이내(33.13m) 위치 데이터(44,370개)에 대한 2차 DBSCAN Clustering에서는 여러 형태의 6개 Cluster( )가 형성되었으며 ε와 minPts를 만족하지 못하는 Noise도 검출되었다. 이는 조차가 큰 서해안의 특성과 조류의 방향에 따른 타원형 분포 형태를 고려 시 일부 밀집도가 낮은 부분에서 검출되으며 통신오류 또는 위치오류로 추정할 수 있다.
)가 형성되었으며 ε와 minPts를 만족하지 못하는 Noise도 검출되었다. 이는 조차가 큰 서해안의 특성과 조류의 방향에 따른 타원형 분포 형태를 고려 시 일부 밀집도가 낮은 부분에서 검출되으며 통신오류 또는 위치오류로 추정할 수 있다.
이와같이 본 연구에서는 수신한 전체 위치 데이터와 이출거리 이내 데이터에서 DBSCAN Clustering을 통해 ε와 minPts를 만족하지 못하는 Noise(통신오류 또는 위치오류)를 검출할 수 있었고 2차 DBSCAN Clustering을 통해 정제된 위치 데이터를 획득할 수 있었다. 이는 위치 데이터의 품질 향상을 위한 기초 자료로 활용할 수 있으며 관리자와 사용자에게 신뢰성 있는 위치 데이터를 제공함으로써 효율적인 등부표 관리 및 항해안전 사고 예방에도 큰 도움이 될 것으로 판단된다.
하지만 본 연구가 가진 한계점으로 특정 해역의 등부표 1기를 대상으로 분석이 제한적으로 수행되어 있어 우리나라 전 해역과 등부표 종류별로 제안된 방안에 대한 검증 과정이 필요할 것으로 판단된다.
따라서 추후 연구에서는 본 연구를 바탕으로 각 해역별, 등부표 종류별로 위치 데이터 품질 향상을 위한 위치 오류 데이터 검출방안에 대해 폭넓은 연구가 필요하다.
Acknowledgements
이 논문은 2023년 해양수산부 재원으로 해양과학기술진흥원의 지원을 받아 수행된 연구임(해양 디지털 항로표지 정보협력시스템 개발(3/5) (20210650)).