9.77톤급 소형어선의 3자유도 구속모형시험을 통한 선속 별 운항성능 추정
Estimation of a 9.77 G/T Small Fishing Vessel’s Operating Performance Depending on Forward Speed Based on 3-DoF Captive Model Tests
Article information
Abstract
본 연구에서는 연안 및 항만 내에서 운항이 빈번한 총톤수 9.77톤급 소형어선을 대상으로 구속모형시험을 수행하고, 선속 별 운항 성능을 추정하였다. 연안 및 항내에서는 소형 어선이 주로 중저속 운항함을 고려하여, 구속모형시험은 8노트 이하에서 수행하였다. 실선을 1/3.5 축소한 모형선을 대상으로 선형예인수조의 프로펠러 단독특성, 저항, 자항추진 시험을 통하여 실선 선속 별 저항추진성능을 추정하였다. 그리고 타 단독특성, 3자유도 정적 및 동적 HPMM 시험을 수행하고 수평면 운항모델 내 유체력 미계수들을 도출하였다. 특히 사항 및 순수 선수동요시험은 2∼8노트 영역에서 수행되었고, 주요 선형 유체력 미계수들이 선속에 따라 현저하게 변화함을 파악하였다. 선형 유체력 미계수들을 Froude 수에 대한 함수화 한 후, 선속 별 시뮬레이션을 통하여 대상 어선의 조종성능을 검토하였다.
Trans Abstract
In this study, a mathematical model of a 9.77 G/T small fishing vessel was established based on captive model tests. The powering and manoeuvring performances of the vessel in the harbor and coastal sea were focused on, so captive model tests were conducted up to the full-scale speed of 8 knots. Propeller open water, resistance, and self-propulsion tests of a 1/3.5-scaled model ship were performed in a towing tank, and the full-scale powering performance was predicted. Hydrodynamic coefficients in the mathematical model were obtained by rudder open water, horizontal planar motion mechanism tests of the same model ship. In particular, in static drift and pure yaw tests which were conducted at a speed of 2 to 8 knots, the linear hydrodynamic coefficients varied with the ship speed. The effect of the ship speed on the linear coefficients was considered in the mathematical model, and manoeuvring motions, such as turning circles and zig-zags, were simulated with various approach speeds and analyzed.
1. 서 론
해상에서 선박 교통량은 항만 및 연근해에 집중되며 특히 항만 근처에서는 소형어선들의 입출항이 빈번하다. 선박들의 안전한 운항을 위하여 소형어선을 포함한 다양한 선종의 운항성능을 설계 단계에서 미리 예측할 필요가 있다. 한편 최근 선박의 무인화, 자율화 추세에 따라, 특히 항만 근처에서 조우하는 선박들의 운항 성능을 사전에 예측하고 이를 자선의 항로 계획, 회피 기동에 고려하는 기술도 요구된다.
소형어선은 해상 교통량에서 많은 비율을 차지하나, 운항성능에 대한 체계적인 분석이 부족한 상태로 건조, 운용되는 경우가 많다. 최근 통계에 의하면 해양사고의 약 70%가 어선과 관련되며, 사고 어선의 65%가 총톤수 10톤 미만의 소형어선이다 (Park and Yeo, 2015). 소형어선의 안전하고 효율적인 운항을 도모하기 위하여 설계 과정부터 저항추진, 조종 등 운항성능에 대하여 보다 정밀한 해석 및 검토가 필요하다.
국내외의 선행 연구 사례를 보면 소형어선의 운항성능에 대한 체계적 연구는 많지 않다. Yoshimura et al. (2003, 2012)에 의하여 길이 20m 이상 어선들의 구속모형시험 기반 시뮬레이션 및 미계수 추정식이 개선된 바 있다. Obreja et al.(2010), Patalong(2012) 에 의하여 하드차인 및 센터킬을 갖는 30m급 어선의 구속모형시험, 조종시뮬레이션이 수행되었다. 국내에서는 Park et al. (2013)에 의한 20톤급 어선의 타형상 개선 및 선속, 조종 시운전, Lee et al.(2018), Kim et al.(2021) 에 의하여 대형 트롤 어선 경험식 기반 운항 시뮬레이션, 최근 Choi et al.(2023) 연구에서 소형어선의 선형 및 타형상에 따른 운항성능을 CFD로 추정한 사례가 있다. 반면, 대형 선박에 대한 조종성능 추정 연구는 이전부터 다양하게 수행되어 왔다. 수학모델 시뮬레이션으로 범위를 한정한다면 Abkowitz (1964), Ogawa & Kasai (1978) 등의 연구에서 전선 모델, 모듈형 모델이 제안된 후, 구속모형시험으로 모델 내 유체력 미계수를 도출하고 조종시뮬레이션을 수행한 여러 연구들이 있으며 (Lee et al., 1997; Kim et al., 2011), 최근에는 전산유체계산을 통하여 미계수를 도출하고 시뮬레이션을 수행한 사례도 있다 (Sung and Park, 2015). 이와 같이 주로 대형 선박에 초점을 두어 진행된 구속모형시험 및 시뮬레이션 기술을 소형 어선에 적용하여 운항성능을 신뢰도 높게 추정하는 응용 연구가 필요하다.
본 연구에서는 국내에서 기 개발된 소형어선 표준선형을 대상으로 프로펠러, 타 각각의 단독특성 시험을 포함한 3자유도 구속모형시험을 수행하였다. 시험 결과를 통하여 대상 실선의 정수 중 선속 별 저항추진 성능을 추정하고, 운항모델 내 유체력 미계수들을 도출하였다. 특히 선속에 따른 주요 선형 유체력 미계수의 변화를 파악하고, 이를 수식화하여 운항모델에 반영하는 방법을 제안하였다. 제안 모델의 시뮬레이션을 통하여 대상 어선의 선속 별 조종성능을 추정하였다.
2. 대상선 및 운항모델
2.1 9.77 G/T 소형어선
최근 국립수산과학원에서 연안어선의 표준선형 개발 연구를 통하여 (Jeong, 2019), 4.99톤급, 9.77톤급 연안 어선에 대한 표준선형이 개발되었다. 해당 기관의 협조를 받아 표준선형 도면을 활용하여 운항모델 연구를 수행하였다. Fig. 1은 국립수산과학원 연구에서 도출된 9.77톤급 연안복합어선의 일반배치도이고, 설계속도는 12노트, 엔진 출력은 480마력이다.
본 연구에서 Fig. 2처럼 실선을 1/3.5 축소한 모형선을 제작하여 구속모형시험을 수행하였다. 대상 실선 및 모형선의주요 제원을 Table 1에 요약하였다.
모형선의 프로펠러 축계는 Fig. 1 일반배치도에 따라 기준선(baseline)과 5.0° 의 경사각을 가지며, 프로펠러는 선체 전후 방향으로 1번 스테이션에 위치한다. 타는 유사 어선들의 실사례들을 참고하여, 횡단면이 직사각형 형상인 스페이드 타로 형상을 일부 수정하였고, 횡면적은 Fig. 1과 동일하다. 타 단면은 NACA0020 형상이다.
2.2 수평면 운항모델
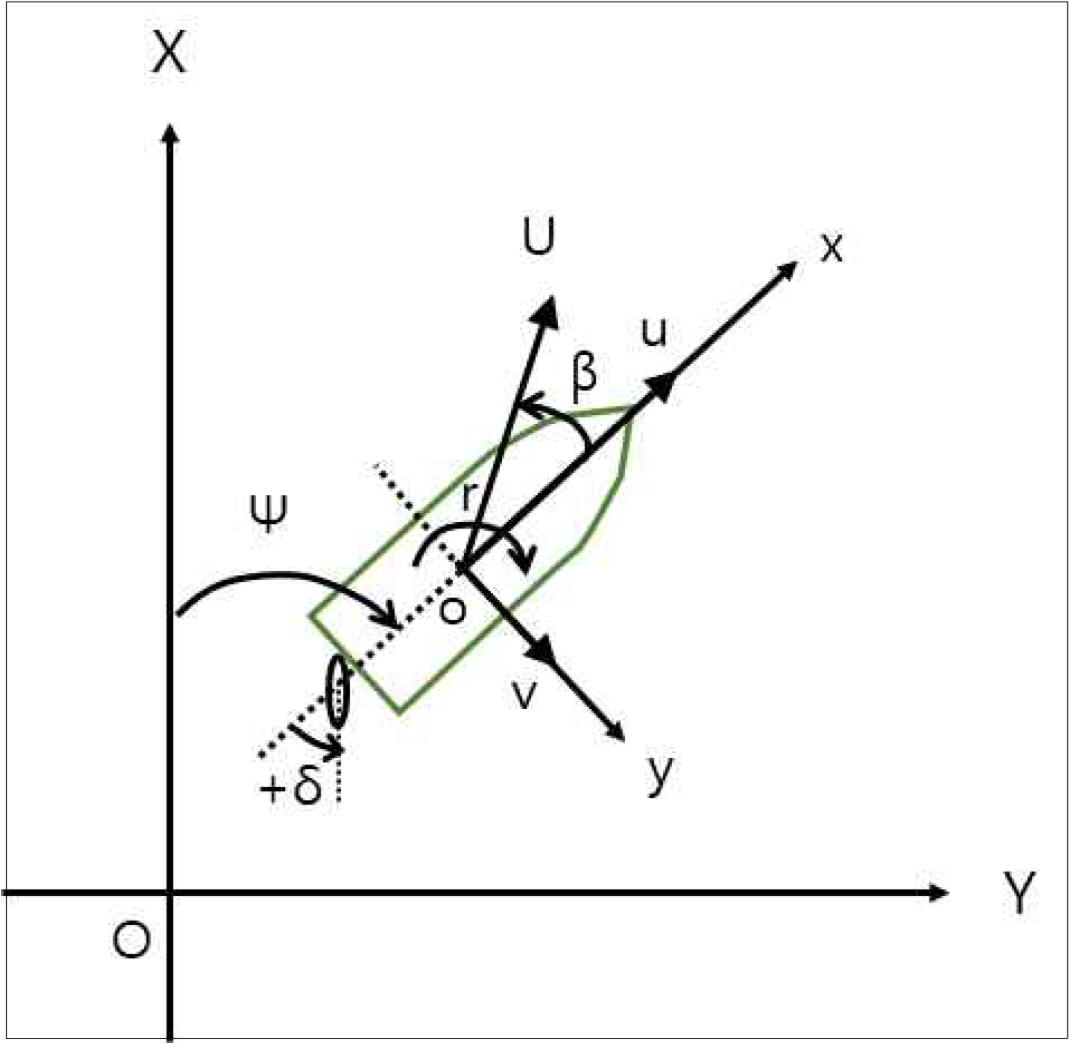
대상선의 수평면 상 거동을 표현하기 위하여 Fig. 3과 같이 공간고정좌표계 O-XY와 선박고정좌표계 o-xy를 설정하였다. 선박고정좌표계 중심 o는 선박의 중앙부(midship), 센터라인, 흘수의 교점에 위치한다. 타각은 선체를 우현 선회시키는 방향, 즉 위에서 볼 때 반시계방향으로 회전하는 각도을 양의 부호로 정의하였다.
식 (1)은 surge-sway-yaw 3자유도 운항모델이며, 우변의 아래첨자 H, P, R는 각각 선체력, 추력, 타력을 의미한다. 각 외력 성분은 구체적으로 식 (2), (3), (4)와 같다.
식 (2)에서 RT는 선체의 전저항이다. 식 (3)에서 t는 추력감 소계수, ρ는 물 밀도, DP는 프로펠러 직경, KT는 프로펠러 추력을 ρn2D4P으로 무차원화 한 계수이며 전진비 JP에 대한 함수이다. 식 (4)에서 tR, aH, xH는 타-선체 간섭계수, FN은 타 직압력, UR, αR은 각각 타유입속도 및 유입각, fα는 타유입각 에 대한 타양력계수 기울기이다. uR, vR 및 uP, vP는 각각 타와 프로펠러 위치에서 전후, 좌우방향 유속 성분이다. ϵ, κ는 타유입속도 관련 미계수, η는 타 전체 횡면적 중 프로펠러 증 속류가 지나는 면적의 비율이다. ϒR, lR은 각각 타 위치의 정 류계수 및 선회각속도 영향에 의한 계수이다. w는 직진 중 프 로펠러 위치의 반류계수, wP는 사항 및 선회 거동 중 변화한 반류계수이다. CP는 반류보정계수이다.
운항모델 내 모든 힘과 모멘트는 식 (5)와 같이 무차원화 한 값으로 변환하여 사용하였다.
2.3 구속모형시험 조건
앞 절에서 소개한 운항모델 내 계수들을 결정하기 위하여 선박해양플랜트연구소 선형예인수조에서 구속모형시험을 수행하였다. 수조 길이, 폭, 깊이는 각각 200 m, 16 m, 7 m 이다.
저항추진 구속모형시험 조건은 Table 2와 같다. 프로펠러 단독특성 (POW) 시험, 저항시험, 자항추진시험으로 구성된다.
POW시험은 프로펠러 전진비 0.0부터 1.1 범위에서 수행되었다. 저항 및 자항추진시험은 실선 기준 8노트까지 수행되었으며, 대응하는 최대 모형선 예인속도는 2.2 m/s이다. 대상 9.77 톤급 어선의 설계속도는 12노트이지만, 원양이 아닌 항내 및 연안에서는 주로 이보다 낮은 속도에서 운항함을 반영하여 본 연구에서는 최대 8노트까지 모형시험을 수행하였다.
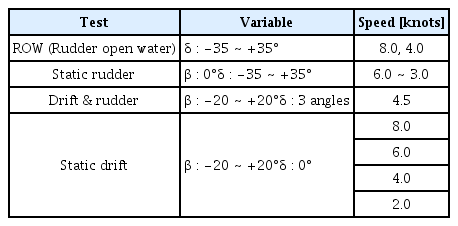
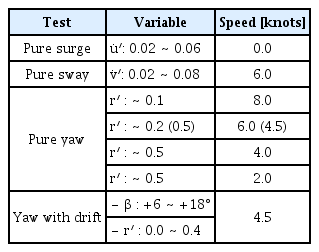
Tables 3, 4에 수평면 조종구속시험 (HPMM; Horizontal planar motion mechanism)의 정적 및 동적시험 조건을 요약하였다. 모형 타의 양력 성능을 정밀 도출하기 위하여 타 단독특성 (ROW; Rudder open water) 시험을 추가하였다. 전체 HPMM 시험은 실선 속도 6노트 기준이며, 선체 주요 선형 미계수를 도출하는 사항시험, 순수선수동요시험의 경우 2∼8노트의 넓은 범위에서 수행하였다.
3. 실선 저항추진성능 추정
3.1 POW 시험 - 프로펠러 단독특성
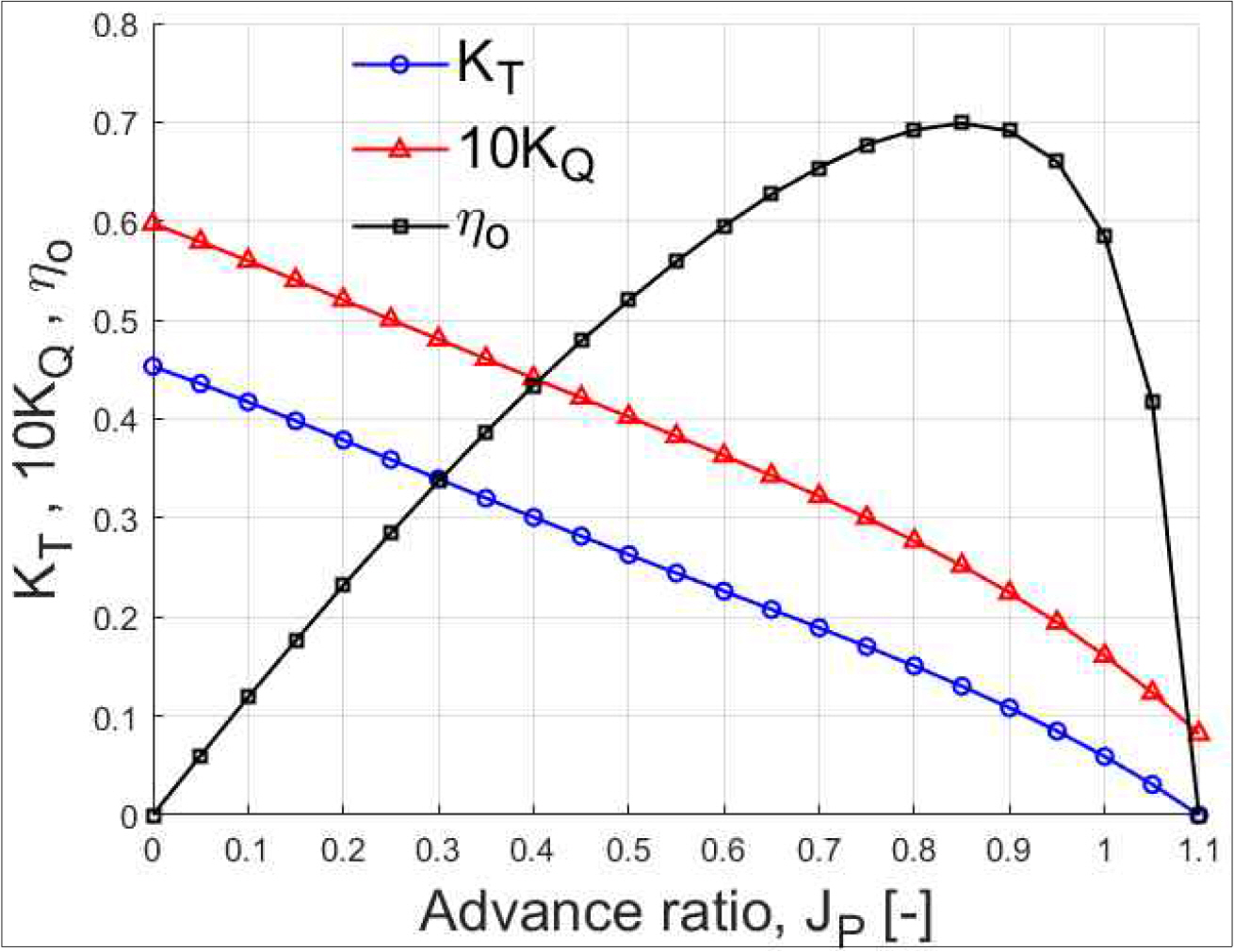
대상 어선의 설계 프로펠러에 대한 POW 시험을 수행하였고, 도출된 추력계수 KT , 토크계수 KQ, 그리고 단독효율 ηo를 전진비에 대하여 나타내면 Fig. 4와 같다. 본 운항모델에서는 추력계수를 식 (6)과 같이 전진비에 대한 2차식으로 근사하여 사용하였다. 2차 근사식 내 계수들은 Table 6과 같다.
3.2 저항 시험 - 실선 유효마력 추정
프로펠러가 없고 타만 장착한 모형선에 대하여 2∼8노트 선속 별 저항시험을 수행하고, 그 결과를 기반으로 실선 유효마력을 추정하였다. 식 (7)과 같이 2차원 확장법을 통하여 모형선 전저항을 마찰저항과 잉여저항으로 분리하고, ITTC 모형선-실선 상관곡선으로부터 실선 마찰저항을 추정하였다. 실선 전저항 계수는 마찰저항계수, 잉여저항계수에 모형선-실선 상관계수 CA를 합하여 도출하였다. CA는 0.000370을 사용하였다. 본 연구에서 공기저항 성분은 고려하지 않았다.
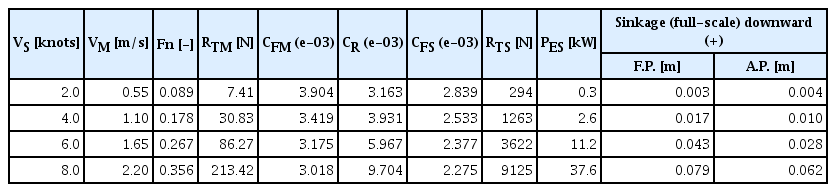
Table 7에 선속 별 계측된 모형선 저항 및 실선 유효마력 추정 결과를 정리하였다. 각 선속 별 저항시험 중 항주자세는 Fig. 5와 같다. 선속이 증가할수록 선체가 침하하며, 특히 선수부가 물에 잠기면서 8노트에 이르면 많은 파가 발생한다.
모형선 원점 기준 침하량(sinkage)은 연직하방을 양의 값, 트림(trim)은 선수흘수에서 선미흘수를 뺀 값, 즉 선수트림을 양의 값으로 각각 정의하였다. Fig. 6에 침하량과 트림 계측 결과를 선속에 대한 그래프로 나타내었다. 선속이 증가하면서 모형선이 꾸준히 침하하고, 선수트림도 증가한다. 대상 어선은 좌우 측면과 후면이 각각 하드차인 및 트랜섬으로 각진 형상이고 선저는 평판에 가깝다. 이와 같은 선저면은 Froude 수 약 1.0 이상의 고속에서 양력으로 부상하기 유리하나, 본 시험 최대 속도인 8노트는 Froude 수 0.356 으로 침하 및 선수트림이 증가하는 영역이다.
하드차인 활주선은 대체로 Froude 수 0.4∼0.5 부근까지 침하하다가 그 이상 선속에서 점차 부상한다. 또한 저속에서 발생한 선수트림은 Froude 수 0.5 부근에서 다시 0이 되고, 이후 고속에서는 선수가 들리는 선미트림을 갖는 것이 일반적이다. 대상 어선의 선저가 평판에 가까운 활주선 형상임을 고려할 때, 설계속도인 12노트인 Froude 수 0.534 까지 침하량은 여전히 큰 양수이고, 트림은 양수나 혹은 0에 가까울 것으로 추정된다.
3.3 자항추진 시험 - 실선 전달마력 및 추진기 회전수 추정
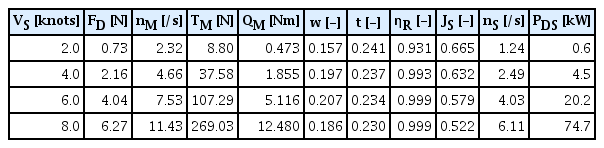
대상선의 자항추진시험을 수행하고 ITTC 1978 실선 성능 추정법에 의하여 실선 전달마력 및 추진기 회전수를 추정하였다(ITTC, 2017). 모형선-실선 마찰저항계수 차이 (skin friction correction) FD를 고려하여 예인하면서 모형선의 선속 별 추력 TM, 토크 QM, 프로펠러 회전수 nM 을 계측하고, 이로부터 반류계수 w 및 추력감소계수 t 를 구하였다. 또한 각 선속 별 추정되는 프로펠러 하중 계수 KTS/J2S 에서 실선 프로펠러의 전진비 JS 를 도출하며, 이에 대응하는 실선 토크 및 전달마력 PDS, 프로펠러 회전수 nS 등을 추정하였다. Table 8과 같다.
본 연구의 운항모델 내에서는 예를 들어 기준 선속 6노트일 때 실선 전저항 RT는 3.62 kN, 추력감소계수 t 및 반류계수 w는 각각 0.234, 0.207, 그리고 대응하는 프로펠러 회전수 nS 4.03 rps 등의 정보를 활용한다.
4. 조종성능 모델링
4.1 ROW 시험 - 타 단독특성
2.1절에서 소개한 바와 같이 직사각형 횡단면 형상의 스페이드 타를 제작하여 모형시험에 활용하였다. 실선 타의 스팬, 코드는 각각 0.98 m, 0.63 m 이며 종횡비 (aspect ratio)는 1.556이다. 타 성능 계측을 위한 타 단독특성 (ROW) 시험 장비는 Fig. 7 과 같으며, 자유수면 영향을 배제하기 위하여 타 상단이 1.0 스팬 길이 이상 물에 잠기도록 설치하였다. 특정 속도로 예인 중 타각에 따른 저항, 양력, 토크를 계측하였다.
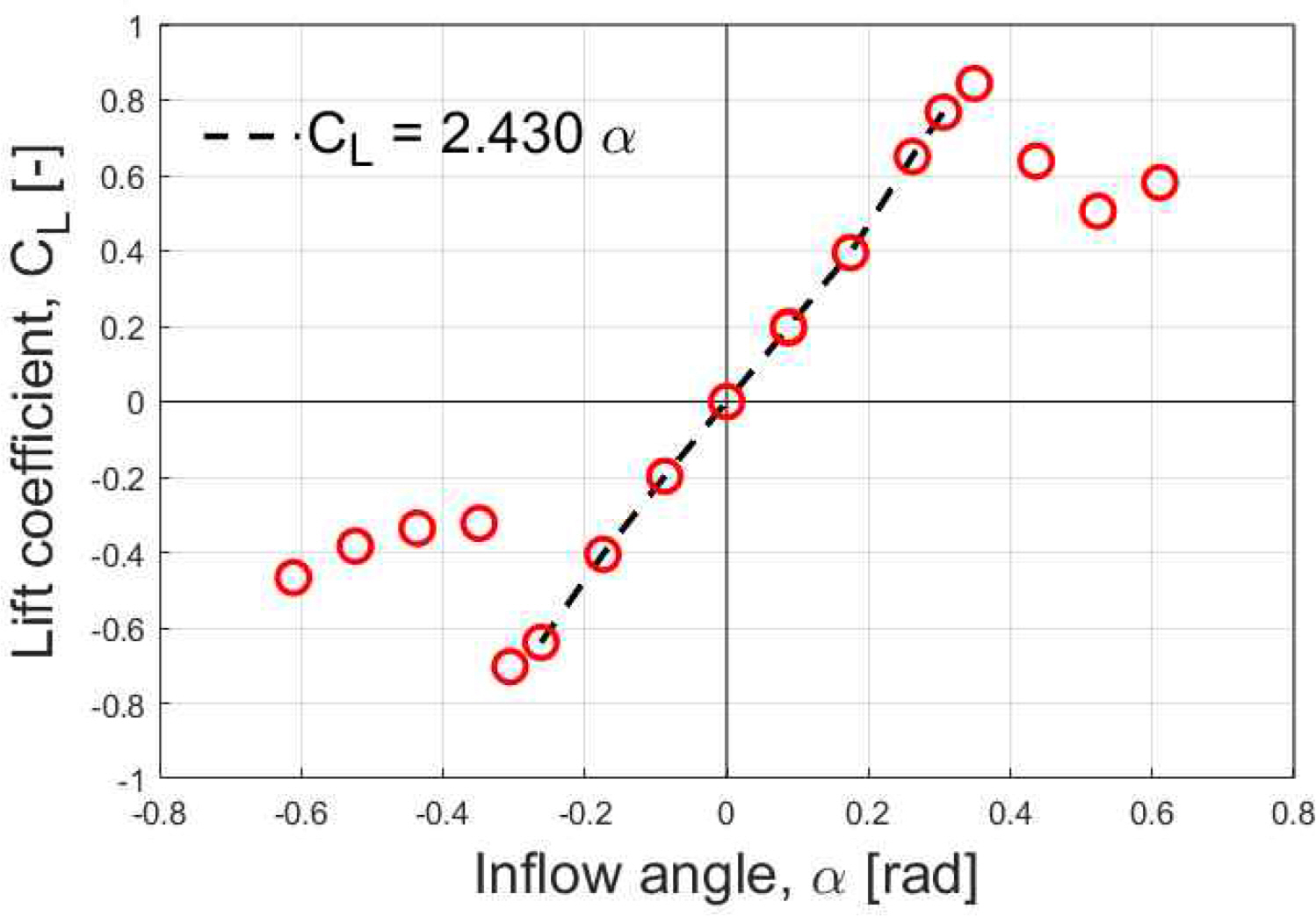
Fig. 8은 ROW 시험에서 계측한 타각 별 양력계수이다. 그래프의 기울기 fα는 2.430 이다. 스페이드 타의 양력계수 기울기는 Fujii (1961) 의 연구에서 추정식이 제안된 바 있으며, 추정식에 의한 값은 2.506 으로 본 ROW 시험 결과와 유사하다. 이하 운항모델에서는 시험 결과인 2.430 을 사용하였다.
4.2 HPMM 시험 - 유체력 미계수
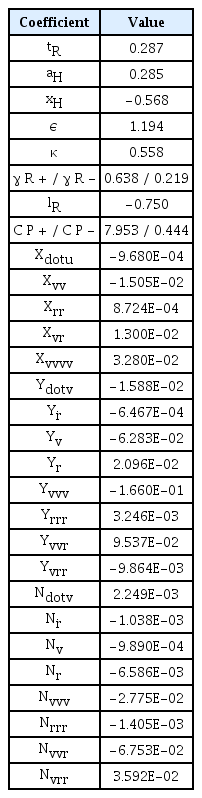
조종성능 관련 미계수들을 도출하기 위하여 Fig. 9와 같이 대상선 6노트 기준 HPMM 시험을 수행하였다. 모형시험에서 도출된 유체력 미계수는 Table 9 와 같다. 모든 미계수는 식 (5)의 방식에 따라 무차원화 된 것이며, 실선 운항모델 내에서도 동일한 무차원 값을 사용하였다.
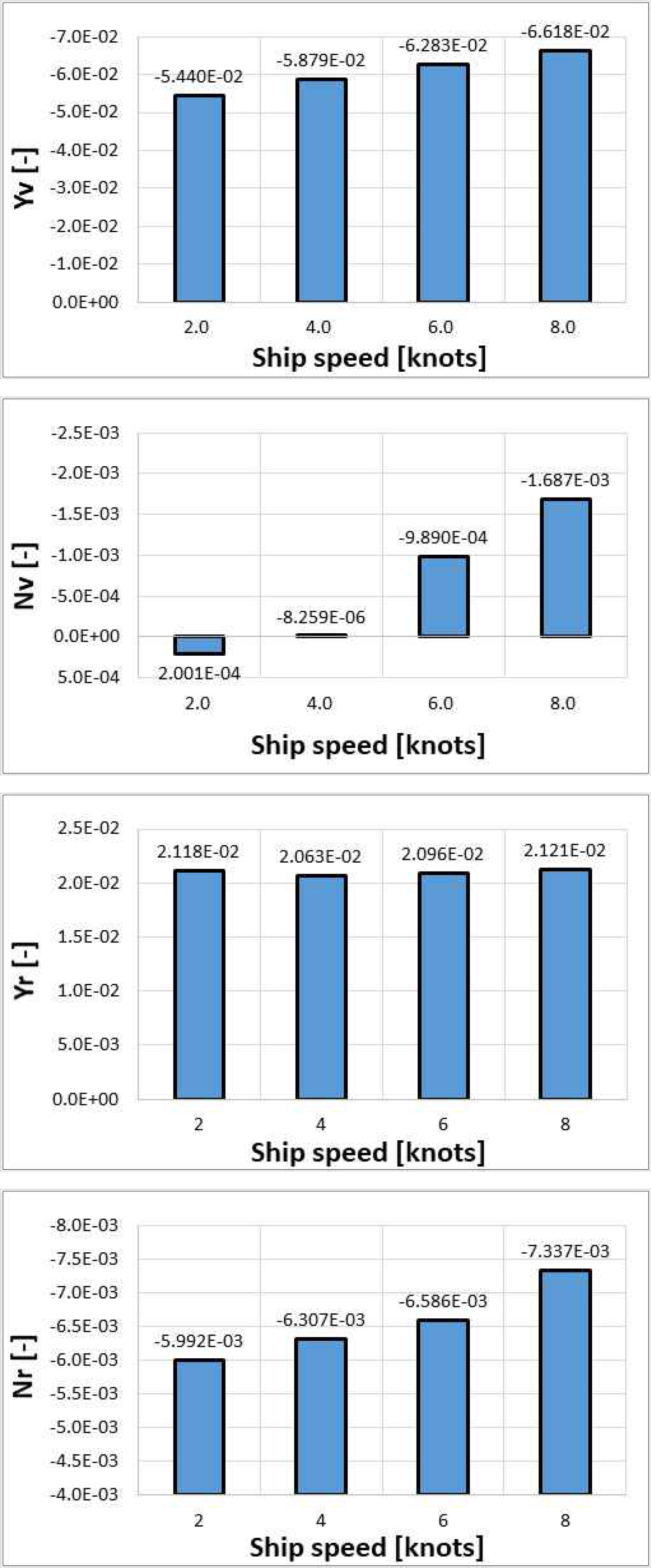
Table 9의 유체력 미계수는 대체로 기준 선속 및 그 부근에서 상수로 간주되나, 선속 별 항주 자세가 Fig. 6과 같이 달라진다면, 특히 선체력 관련 미계수들도 선속에 따라 변화할 수 있다. 2∼8노트 영역에서 수행된 사항시험 및 순수선수동요시험으로 도출된 선속 별 주요 선형 미계수는 Fig. 10과 같다.
Yr 은 큰 변화가 없으나, Yv, Nv, Nr 은 선속이 증가할수록 뚜렷하게 음으로 감소하는 경향을 보인다. Fig. 6에서 선속이 높아지면서 선체가 꾸준히 침하하였고, 수면 아래 선체 침수 횡단면적이 증가하면서 Yv, Nr의 절대값이 커진다. 더불어 선속이 높아질수록 선수트림에 의하여 선수부 침수부피가 늘어나고 유체력 중심도 선수 쪽으로 이동하면서 Nv의 절대값이 커지는 것으로 분석된다.
주요 선형 미계수의 변화에 따라 선속 별 직진안정성 및 조종성능이 달라지며, 정밀한 운항모델을 위하여 이와 같은 선속 별 운항성능 변화를 추가 고려할 필요가 있다.
4.3 주요 선형 유체력 미계수의 선속 영향 반영
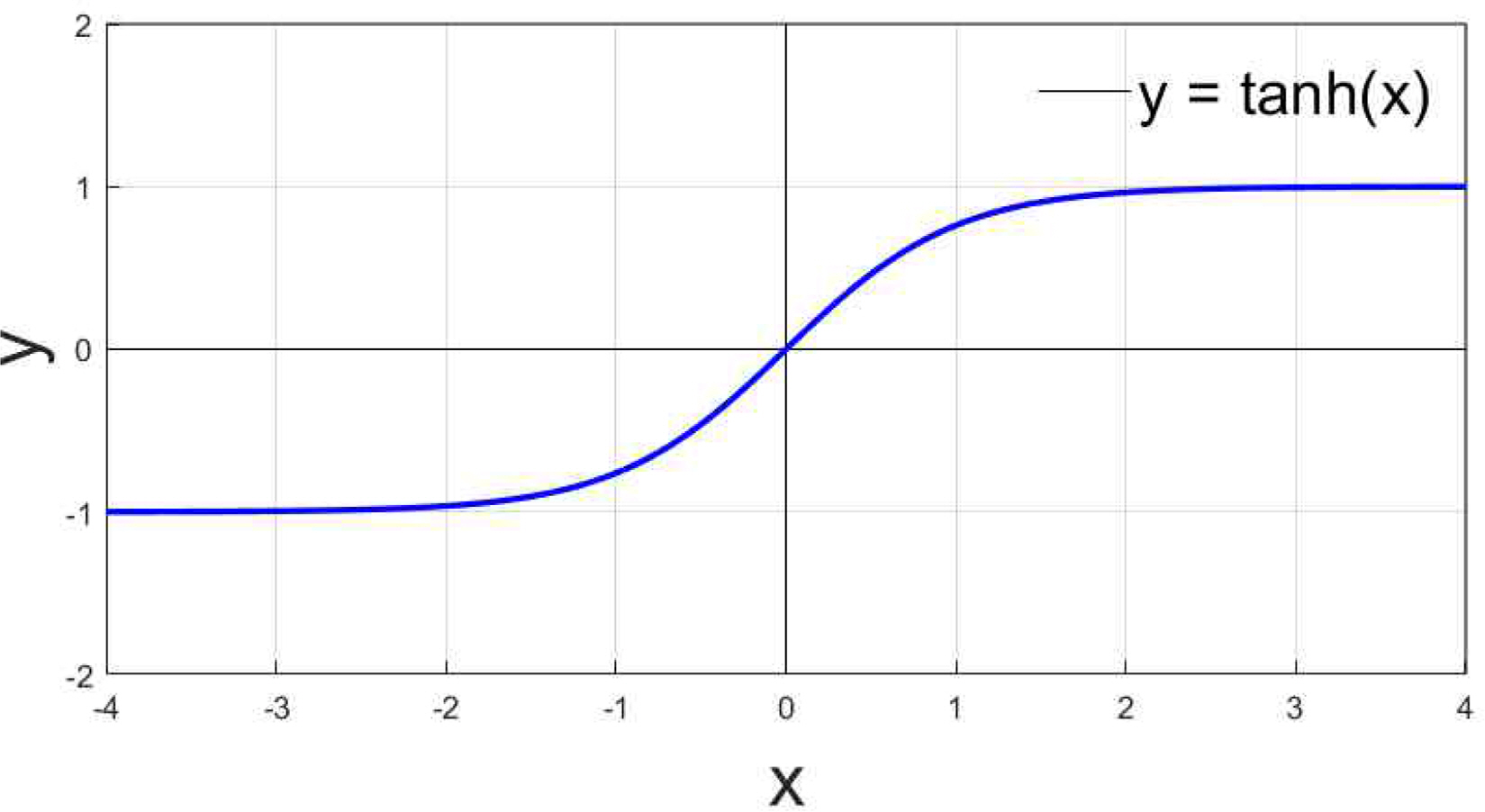
Fig. 11은 hyperbolic tangent 함수 그래프이다. (0, 0) 원점을 지나고, 원점을 대칭으로 x가 감소, 증가할수록 y 값이 각각 -1과 1에 수렴하는 형태이다.
Hyperbolic tangent 함수를 활용하여 선형 미계수 Yv, Nv, Nr을 각각 Froude 수에 대하여 함수화하기로 한다. 3.2절과 같이 대상 어선의 설계속도인 12노트까지 침하량은 양수로 조금 더 증가, 트림은 양수, 혹은 0에 가까운 값이 예상된다. 따라서 선형 미계수들도 8노트 값을 기준으로 12노트까지 거의 유사하거나, 혹은 조금 더 음으로 감소할 것이다. 한편 2노트 이하 저속에서는 항주 자세 변화가 거의 없고, 2노트 미계수를 그대로 사용하여도 무방하다.
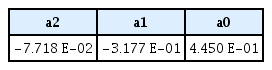
각 미계수들은 중속 6노트 (Fn = 0.267)에서의 미계수를 기준으로 그 이하에서는 2노트 (Fn = 0.089)의 값으로 수렴하고, 그 이상에서는 12노트 (Fn = 0.534)까지 절대값이 완만하게 증가하면서 수렴하는 형태이다. Hyperbolic tangent 함수 원점을 각 미계수의 6노트 값으로 이동시킨 후, 적절한 계수를 추가하여 Fig. 12처럼 Froude 수에 대한 함수식을 생성하였다. 최종 도출된 수식은 Table 10과 같다.
5. 제안 모델을 활용한 실선 조종성능 추정
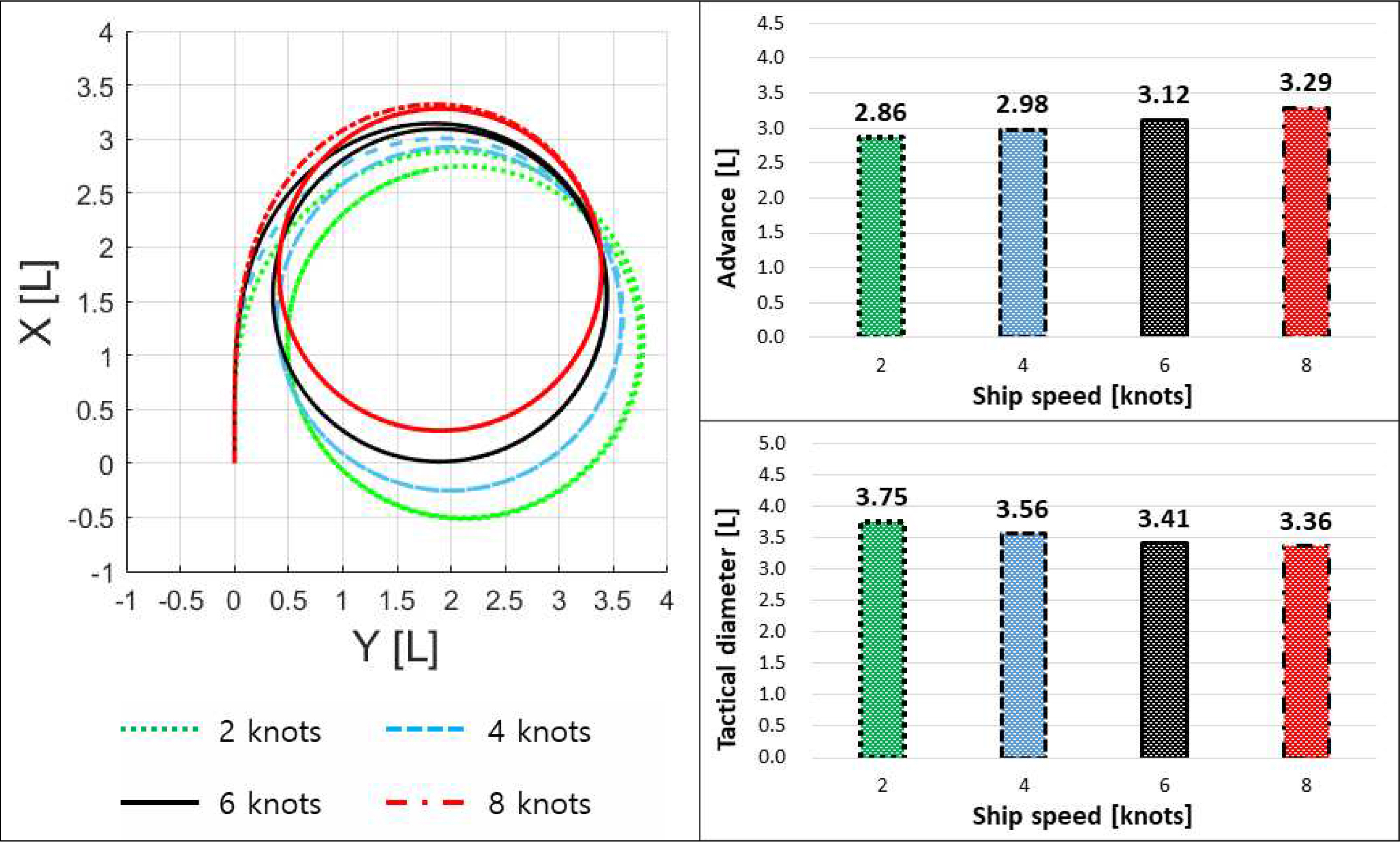
제안된 모델을 활용하여 대상 실선의 초기속도 2∼8노트에 대한 35° 우현 선회, 10°/10° 우현 지그재그 시뮬레이션을 수행하였다. 타 각속도는 4°/s 로 설정하였다. 조종성능 시뮬레이션 결과는 Figs. 13, 14 와 같다.
선속이 높을수록 선회 중 전진거리는 증가, 전술직경은 감소한다. 그리고 지그재그 중 1차, 2차 오버슈트각은 꾸준히 증가한다. 만약 주요 선형 미계수의 선속 영향을 고려하지 않는 경우에도 시뮬레이션 상에서 성능 지수들의 변화는 예측되지만 그 변화량은 상대적으로 적으며 본 결과와 차이가 있다. 제안한 모델을 통하여 선속 별 변화하는 유체력을 보다 사실적으로 추정하고, 이를 통하여 조종성능 시뮬레이션 정확도가 향상되었을 것으로 사료된다. 다만 향후 자유항주 모형시험, 실선 시운전 등을 통하여 모델의 정량적인 검증이 필요하다.
6. 결 론
본 연구에서는 총톤수 9.77톤급 소형어선을 대상으로 연안 및 항내 운항 선속에 초점을 둔 저항추진 및 조종 구속모형시험을 수행하고, 시험 결과에 기반하여 선속 별 조종성능을 추정하였다. 주요 결론은 다음과 같다.
· 대상 어선의 저항추진성능을 추정하기 위하여 최대 8노트 선속에 대하여 POW, 저항, 자항추진시험을 수행하였다. 프로펠러 단독특성, 실선 유효마력, 전달마력, 추진기 회전수 등을 추정하고, 운항모델에 활용하였다. 선속이 높아질수록 대상선의 침하 및 선수트림이 증가함을 확인하였다.
· 대상 어선의 조종성능을 추정하기 위하여 선속 6노트에 초점을 둔 ROW 및 HPMM 정적, 동적시험을 수행하였다. 타 단독특성 및 운항모델 내 유체력 미계수들을 도출하였다.
· 8노트 이하에서 선속 별 수행된 사항 및 선수동요시험으로부터 선속에 따른 주요 선형 유체력 미계수의 현저한 변화를 확인하였다. 운항모델 내 선형 유체력 미계수를 선속에 대하여 함수화하고, 시뮬레이션을 통하여 선속 별 조종성능 변화를 검토하였다.
본 모형시험에서 도출된 유체력 미계수의 무차원 값은 하드차인과 센터킬을 갖고, 길이-폭 비 등 제원이 유사한 타 소형어선의 성능 추정에도 참고 자료로 활용될 수 있다. 다만 수행된 조종모형시험은 중저속 영역의 수평면 거동에 한정되므로, 고속 운항 중 횡동요 등을 다룰 경우 추가 시험 및 해석이 요구된다.
향후 자유항주 모형시험, 혹은 시운전 정보를 활용하여 제안한 운항모델의 정밀도를 검증하는 것이 바람직하다. 또한 모델의 선속 적용 범위 및 자유도를 확장하는 연구도 필요할 것이다.
Acknowledgements
본 연구는 산업통상자원부 및 산업기술평가관리원 연구비 지원으로 수행된 ‘자율운항선박 기술개발사업(20011689, 자율운항 지능형 시스템 실증 및 성능시험 개발(PNS4610))’ 연구결과입니다. 대상 어선의 도면 및 정보를 공유해 주신 국립수산과학원 정성재 박사님께 감사드립니다.