Pallet Size Optimization for Special Cargo Based on Neighborhood Search Algorithm
Article information
Abstract
A pallet, typically a form of tertiary packaging, is a flat x`structure used as a base for the unitization of goods in the supply chain. Standard pallets, such as T-11 and T-12, are used throughout the logistics industry to reduce the cost and enhance the efficiency of transportation. However, it is impossible to handle special cargo using a standard pallet due to its size and weight, so customized pallets have been developed and are now in use. This study suggests a pallet size optimization method to calculate the optimal pallet size, which minimizes the loss of space on a pallet. The main input features are the specifications and the storage quantity of each cargo, and an optimization method that modified the Neighborhood Search Algorithm calculates the optimal pallet size. A comparative analysis was conducted through simulation to verify the optimality of the developed algorithm.
1. Introduction
A pallet is a device that serves as a platform for carrying cargo and allows for transporting multiple pieces of cargo as a single unit(NLIC, 2023). In logistics, pallets are used as a basis for handling, stacking, storing, loading, and transporting goods and cargo. Additionally, pallets are a fundamental and essential element for logistics efficiency, as they significantly impact all industries, from raw material procurement to consumer delivery(Kim et al. 2009).
Pallets can be classified by their material, such as wood, plastic, paper, or steel, and their dimensions can vary depending on their purpose and the industry they are used. In South Korea, the standard pallet dimensions for unit load transportation were revised in late 2013(KS T0006), which included 1,200mm x 1,000mm (T-12 type) in addition to the 1,100mm x 1,100mm (T-11 type) that had been used as a national standard until then (Kim, 2014). The ISO international standard pallet dimensions include 1,219mm x 1016mm (US standard), 1,200mm x 800mm (commonly used by 18 European countries), 1,165mm x 1,165mm (Australian standard), and 1,140mm x 1,140mm (for maritime use).
There are clear advantages when using these standardized pallets, such as cost savings through consistent transport, standardization of trade units, efficiency advancements in transportation operations, and working conditions for loading and unloading operations. However, when handling special cargo, it is common to use customized pallets due to the limitations regarding their size and weight.
Special cargo refers to goods that require special attention during transportation and are transported according to separate handling procedures(Baek, 2020). These include dangerous goods, valuable goods, heavy and oversized cargo, fragile cargo, live animals, and other cargo that exceeds typical levels in terms of properties, shape, weight, price, etc.
In the case of handling special cargo, appropriate transport equipment has been developed and used according to the characteristics of the cargo in order to minimize the damage that occurs during transportation. In addition, for heavy and oversized cargo such as automobile parts and large machinery, it is generally impossible to load them onto standardized pallets due to their weight and size. Therefore most companies are now using their own customized pallets.
Customized pallets that are currently being used in the industry, can be divided into civilian and military use. In the civilian sector, logistics equipment companies such as Helper TLS developed glass-specific pallets and roll pallets. The glass-specific pallets, including A-Frame, L-Frame, and Stillage, are shock-mounted which allows stable transportation of the fragile glass plates. On the other hand, the roll pallets are designed specifically to store cylindrical films and are produced in detachable and attached variable types. Other companies have introduced different types of pallets for handling special cargo, such as the Multiple Transport Platform, a heavy-duty pallet designed for transporting high-end automobiles by air, and the Coil Deck, a coil-specific pallet that minimizes damage to coils using rubber pads.
For military use, the 436L Master Pallet(HCU-6/E), currently in use by the US Air Force, is an air cargo and military goods-specific pallet designed to be loaded and unloaded on military transport planes and Civilian Reserve Air Fleet(CRAF) cargo planes. The pallet's specifications include the size that is more than four times larger than that of the international standard pallet at 2,235mm x 2,743mm and a maximum load capacity of 4.5 tons.
Even though various customized pallets are designed to match the cargo's characteristics, only the cargo's size and weight are taken into consideration. However, as space utilization directly affects the efficient allocation of resources, it is necessary to determine their size considering the loss of space. By doing so, it becomes possible to maximize the use of available space, ensuring that the available area is utilized to its full potential. As a result, this can lead to cost savings by minimizing wasted space and reducing the number of pallets required.
For this reason, this study aims to compare the total loss space incurred by loading all quantities of specific special cargo and to derive the optimal pallet size that minimizes the loss of space. The optimization algorithm was designed by modifying the neighborhood search technique, and the optimality of the proposed method was verified by confirming the derivation of the global optimal solution through simulation. It is expected that minimizing the loss of space generated when using pallets will not only improve space utilization but also reduce the time and cost required to handle special cargo.
The structure of the paper is as follows. Chapter 2 describes related previous studies, explains the limitations of the previous studies and the direction of this study. Chapter 3 defines the pallet size optimization problem and proposes the optimization algorithm to solve it. Chapter 4 describes the input/output data composition for the simulation and verifies the optimality of the proposed method through simulation. Finally, Chapter 5 discusses the conclusion and implications of the study.
2. Literature Review
2.1 Related Studies
Efforts to minimize the loss of space caused when using standardized pallets have led to many studies on standardization and optimization of packaging container sizes considering pallet loading efficiency.
Morabito et al. (2000) applied an optimization model to the problem of loading products onto a pallet and placing the pallet within a transport vehicle, discussing an approach to optimize the size of the packaging box, pallet, and transport vehicle.
Suh et al. (2005) proposed an integrated packaging container size that can be used for various agricultural products by comparing and evaluating the pallet loading efficiency between the standard agricultural packaging size and the plastic packaging container size using Monte Carlo simulation techniques.
Jung and Han (2015) investigated the pallet loading patterns used in a warehouse-type discount store(Membership Wholesale Club, MFC) that displays products on pallets and proposed a standard specification for a Retail Ready Package(RRP) that can improve the loading efficiency of the block loading method.
For pallets for special cargo that can not be loaded on standardized pallets, research related to material and structural design that suits the characteristics of the product is mainly conducted in an effort to minimize the cost and the damage during storage.
Park et al. (2008) aimed to find the number of boards required to load a certain number of coils using the First-Fit Decreasing algorithm to minimize the number of pallets required.
Li et al. (2017) proposed an optimal design method for heavy-duty pallet systems based on reliability theory and compared the Modulus of Elasticity (MOE) and Modulus of Rupture(MOR) of various materials. The result showed that Laminated Veneer Lumber(LVL) is the ideal pallet material.
2.2 Limitation of the Previous Studies
When looking at the previous researches, we see that it has focused on standardizing and optimizing the dimensions and specification of packaging containers considering the pallet loading efficiency. However, all of these assume the use standardized pallets with fixed size, so that the affects of the pallet size has on storage and transport were not taken into account. In the case pallets for special cargo, researches only discuss the structural design that matches the product's characteristics, and there is a lack of research that focuses on optimizing pallet sizes and its relationship with space utilization.
Therefore, this study aims to compare the total pallet loss space according to the size of the pallet and to derive the optimal pallet size that minimizes the loss space, taking into account the type, size, weight, and quantity of special cargo stored in limited spaces.
3. Pallet Size Optimization
3.1 Problem Description
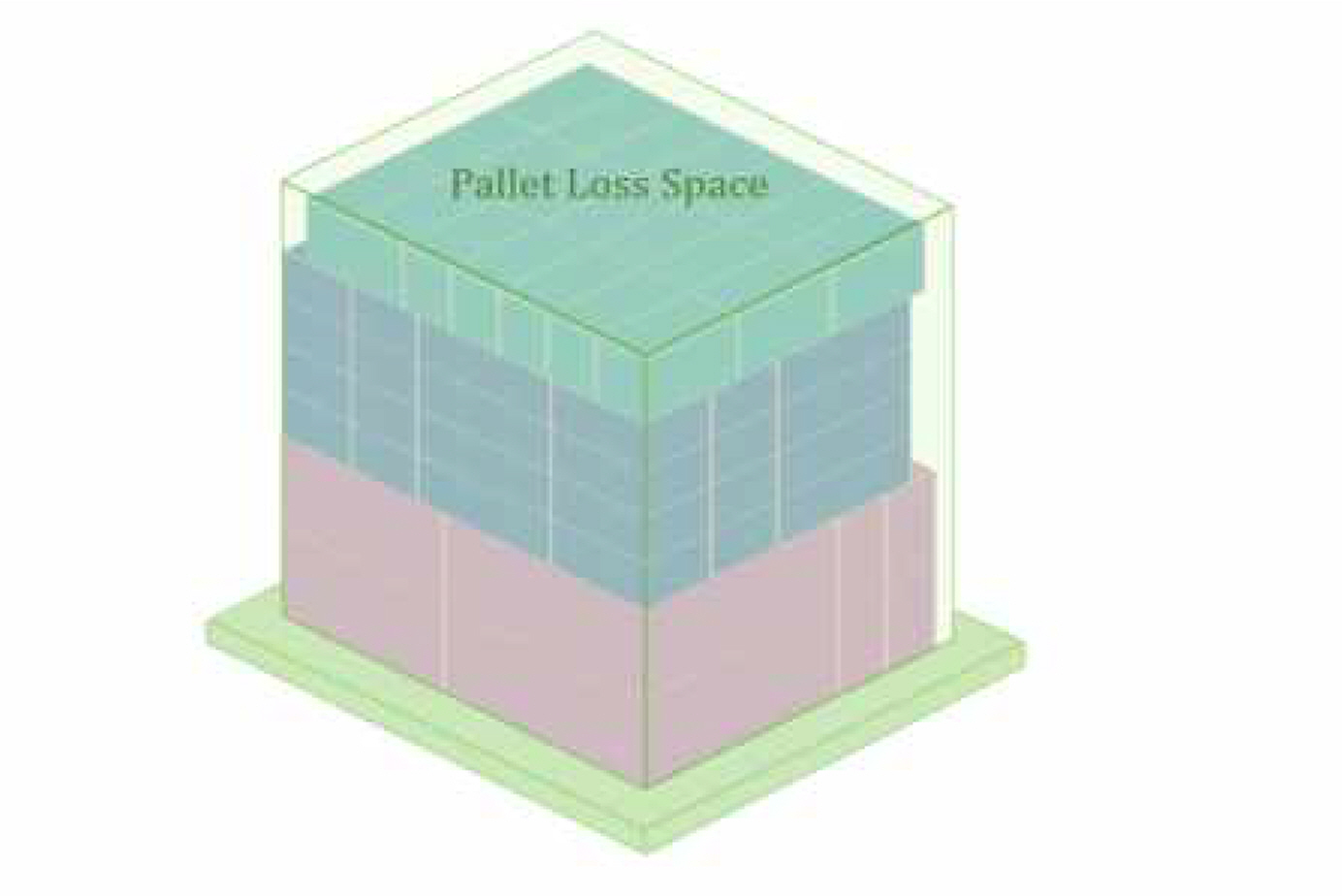
When loading cargo onto pallets, loss of space occurs depending on the stacking method. The loss space on a single pallet is determined by the size of the cargo, the stacking direction and method. The total loss space is determined by the storage quantity, which determines the number of pallets required.
Loss space when loading a pallet
In this study, we aim to solve the problem of optimizing the pallet size to minimize the total loss space required for loading all quantities of cargo for various types of specialized cargo, assuming only one type of cargo can be loaded onto a single pallet.
3.2 Objective Function and Constraints
The objective function and constraints of the pallet size optimization problem with pallet length Lpal and width Wpal as the determinant variable are defined as follows.
i: Special Cargo Type
I: Number of Special Cargo Type
Lpal: Pallet Length
Wpal: Pallet Width
TLS(Lpal, Wpal): Total Loss Space
LSi (Lpal, Wpal): Pallet Loss Space of Special Cargo i
Qpali (Lpal, Wpal): Number of Required Pallets for Special Cargo i
Nxi (Lpal, Wpal): Number of Special Cargo i stacked in x axis
Nyi (Lpal, Wpal): Number of Special Cargo i stacked in y axis
Nzi (Lpal, Wpal): Number of Special Cargo i stacked in z axis
ni (Lpal, Wpal): Stackable Quantity per Pallet for Special Cargo i
Hpalmax: Maximum Height
Gpalmax: Maximum Load Capacity
Li: Length of Special Cargo i
Wi: Width of Special Cargo i
Hi: Height of Special Cargo i
Gi: Weight of Special Cargo i
C: Clearance Distance
The objective function in Equation (1) represents the total loss space according to the pallet size and aims to derive the pallet length and width that minimize it. Constraints (2) and (3) limit the pallet length and width to their allowable ranges, respectively. Constraints (4) and (5) show that the minimum clearance distance that are required for cargo stowage should be considered. Constraint (6) indicates the maximum height for loading cargo onto the pallet, and Constraint (7) indicates that the total weight of the cargo loaded onto the pallet cannot exceed the maximum load capacity of the pallet.
3.3 Pallet Size Optimization
In this study, calculation of the total loss space according to the size of the pallet is repeatedly done, and a modified neighbor search algorithm is used to search for the optimal pallet size that minimizes the total loss space.
3.3.1 Calculation of the total loss space
The process of calculating the total loss space based on the pallet size is shown in Fig. 2.
Total Loss Space calculation procedure
1) Set the initial pallet length and width
Firstly, the initial values for the length and width of the pallet are set within the user-defined allowable range.
2) Select the appropriate stacking method
After the pallet size is set, an appropriate stacking method is selected for each type of cargo based on its specifications. The number of cargo or containers stacked in the direction of the x axis(length) and the y axis(width) is determined, considering the maximum loading limit height of the pallet. The number of cargo stacked in the direction of the z axis(height) is then determined by considering the loading capacity and clearance distance of the pallet.
3) Calculate the stackable quantity per pallet
The stackable quantity per pallet for each type of cargo is then calculated by multiplying the number of cargo stacked in the direction of the x axis, y axis, and the z axis determined in the previous step.
For special cargo loaded in containers, the user-defined quantity of cargo that can be loaded into each container is multiplied by type to indicate the quantity of cargo that can be loaded onto a single pallet.
4) Calculate the number of required pallets
The required number of pallets is calculated by dividing the user-defined storage quantity of the special cargo by the stackable quantity per pallet for each type of cargo
where Qreqi notes the storage quantity of special cargo i
5) Calculate the loss space for each type of cargo and the total loss space
The loss space for a single pallet of a given type of cargo is calculated by subtracting the volume occupied by the cargo from the total space available on the pallet.
The total loss space is calculated by adding up the loss space for each type of cargo, multiplied by each required number of pallets.
3.3.2 Proposal of the modified Neighborhood Search algorithm
The Neighborhood Search algorithm is a method of improving solutions by iteratively searching for neighboring solutions from an initial solution, and is classified into Hill-climbing search, Simulated Annealing, and Tabu search, etc(Glover and Laguna, 1997; Kang, 2004). As many real-world optimization problems are nonlinear and non-convex, meaning the objective function may have multiple local optima or suboptimal solutions. Neighborhood Search Algorithms, with their ability to explore and exploit the local search space, can navigate through these complex landscapes and identify good solutions even in the presence of multiple optima. Furthermore, Neighborhood Search Algorithms offer flexibility in problem representation and solution search. They can be applied to a wide range of optimization problems, including combinatorial optimization, continuous optimization, and mixed-integer optimization. Additionally, these algorithms can be adapted and customized to incorporate problem-specific constraints, objectives, and solution representations. Therefore, Neighborhood Search algorithm was applied among various heuristic techniques to compare the total loss space and to derive the optimal pallet size.
Among them, Hill-climbing search is a method that repeats the search until there is no better neighboring solution than the current solution, using the steepest ascent strategy to select the best solution among all neighboring solutions. Although this particular method has a relatively simple structure, it has the disadvantage of terminating when it reaches a local optimum or when all neighboring solutions have the same value, even though a better solution exists globally(Hwang, 2009).
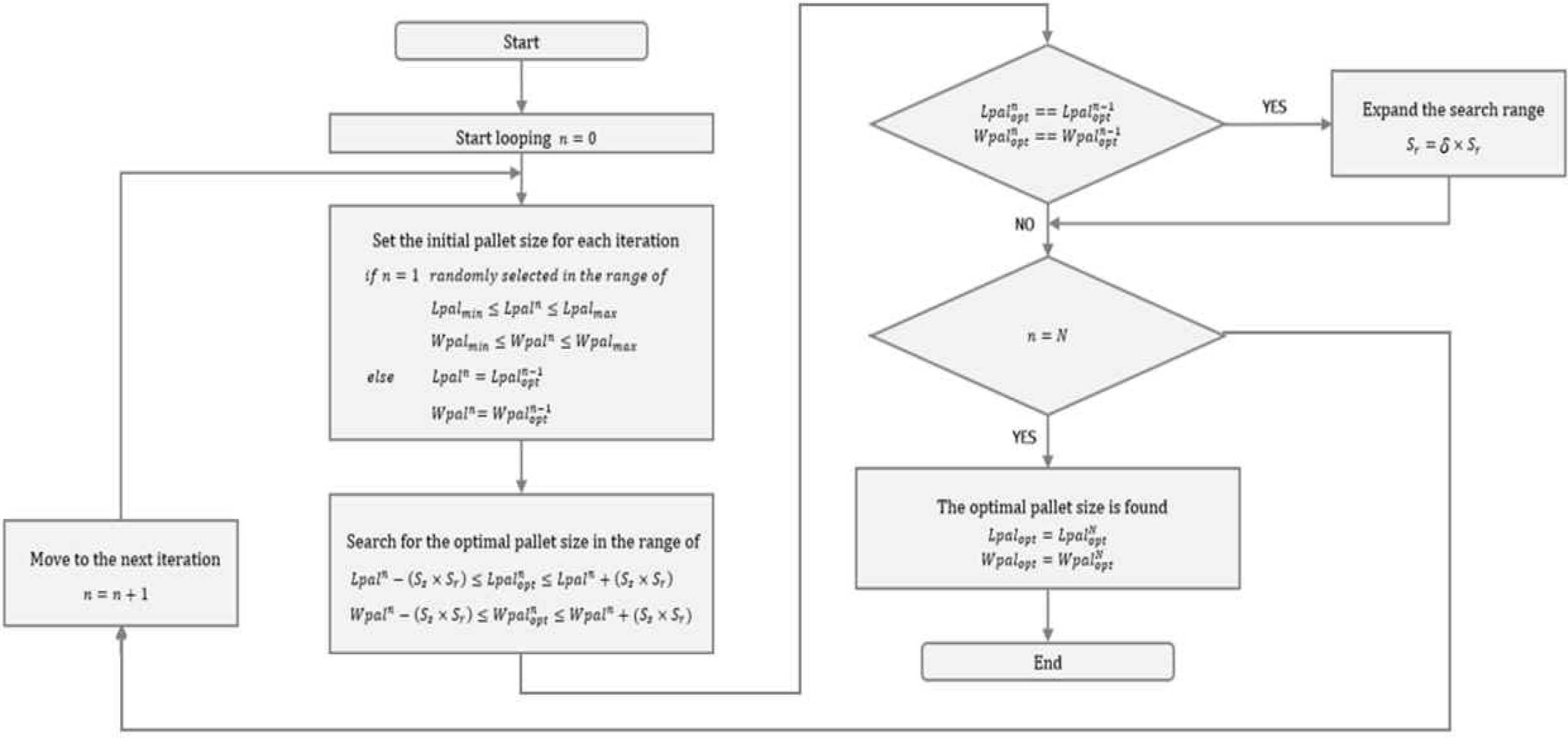
In this study, the traditional Hill-climbing search(steepest ascent strategy) method is modified to enable the search for the global optimal solution and to select the optimal pallet size as shown in Fig. 3.
Search algorithm for the optimization of the pallet size
First, the total loss space of all neighboring pallet sizes within a specific range is calculated based on the pallet size that corresponds to the initial solution. The pallet size that shows the minimum loss space is selected and becomes a current solution. This process is repeated for a specified number of times and if the objective function value of the neighboring solution is better than the current solution, the search continues by changing the current solution to the neighboring solution. Unlike the traditional Hill-climbing search, if the objective function value of the neighboring solution is greater than or equal to the current solution, the search is not terminated, but the optimal pallet size corresponding to the global optimal solution is calculated by expanding the search range. As a result, the proposed algorithm is capable of finding the optimal length and width of the pallet within the allowable range.
4. Simulation and Optimality Verification
4.1 Simulation Environment
In this study, a pallet size optimization module using MATLAB software was developed to simulate and apply the proposed algorithm to real-world cases. The optimization module was then implemented using the following hardware and operating system: Windows 10 Pro, AMD Ryzen 5 4600G with a Radeon Graphics 3.70 GHz processor, NVIDIA GeForce RTX 3060 Ti, and 32 GB of RAM. Users can run the program and input data regarding the specifications and storage quantity of special cargo by type, as well as constraint-related information. The optimization module then calculates the optimal pallet size that minimizes the total loss space based on the input data. The output module is designed to display the optimal pallet size information, the stackable quantity information, and the pallet loss space information as the result of the optimization module.
4.2 Input and Output Data Composition
4.2.1 Input data
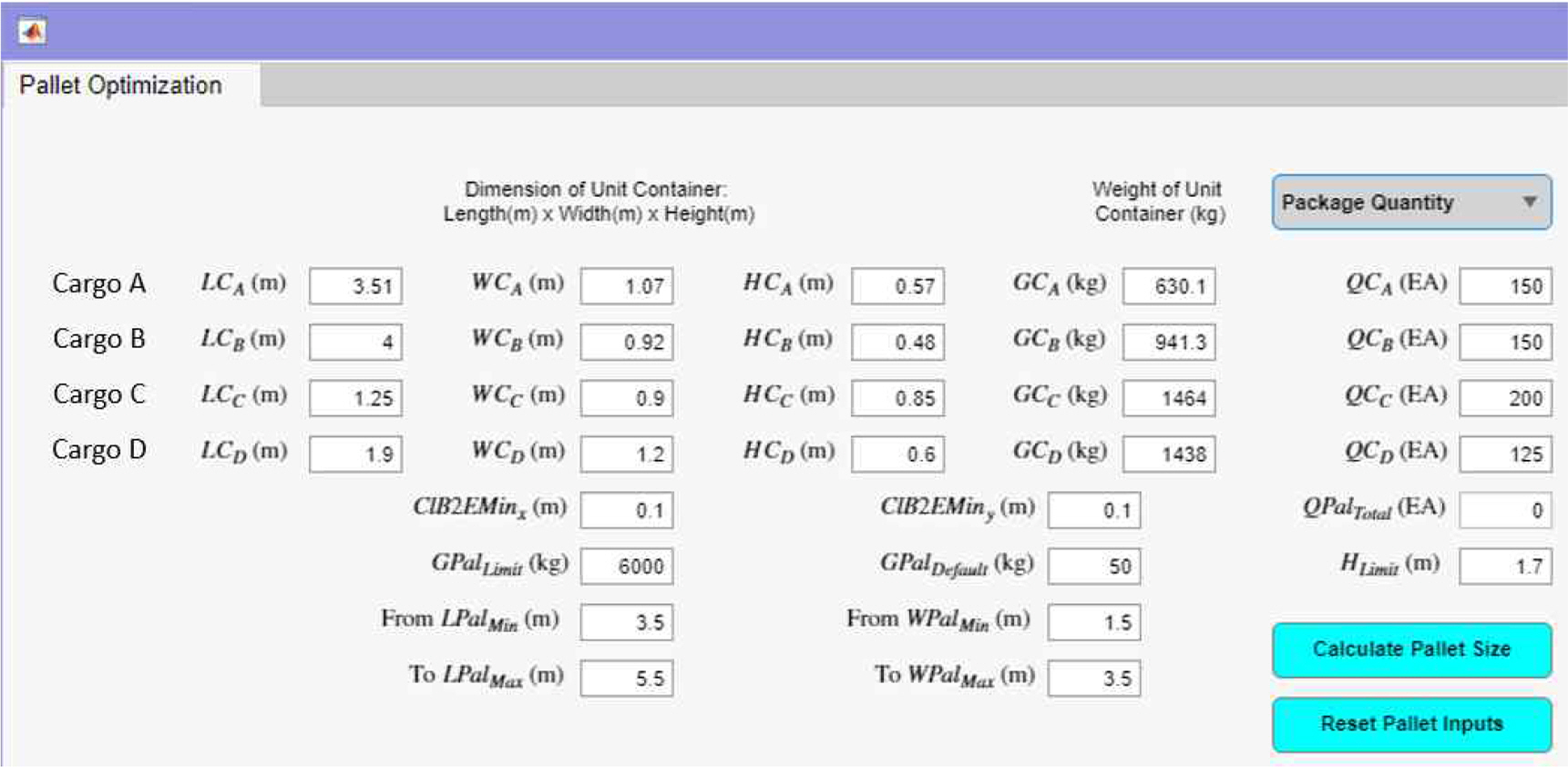
When the program is executed on a Window, the interface of the input module is displayed on the screen. Users can directly input and modify the information for each item through the input window of the interface.
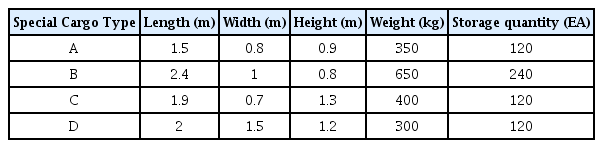
Input data is divided into special cargo specifications and storage quantity information by type, and constraint-related information. The special cargo specification information is composed of the length, width, height, and weight of the cargo. For special cargo loaded in containers, the specifications of the packaging container used should be also entered, and the loading capacity inside the packaging container should be priorly set.
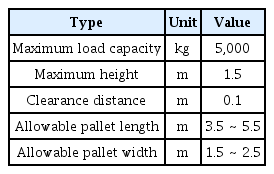
After completing the configuration of special cargo specification and storage quantities, constraint-related information for the pallet should be entered. The related input data includes the maximum load capacity and maximum height of the pallet, the clearance distance between the pallet edge and the cargo, and the allowable range of the pallet length and width.
Input interface of the optimization module
Pallet size optimization module
Input features of the optimization algorithm
4.2.2 Output data
The output data are the optimal pallet size information, stackable quantity information, and pallet loss space information.
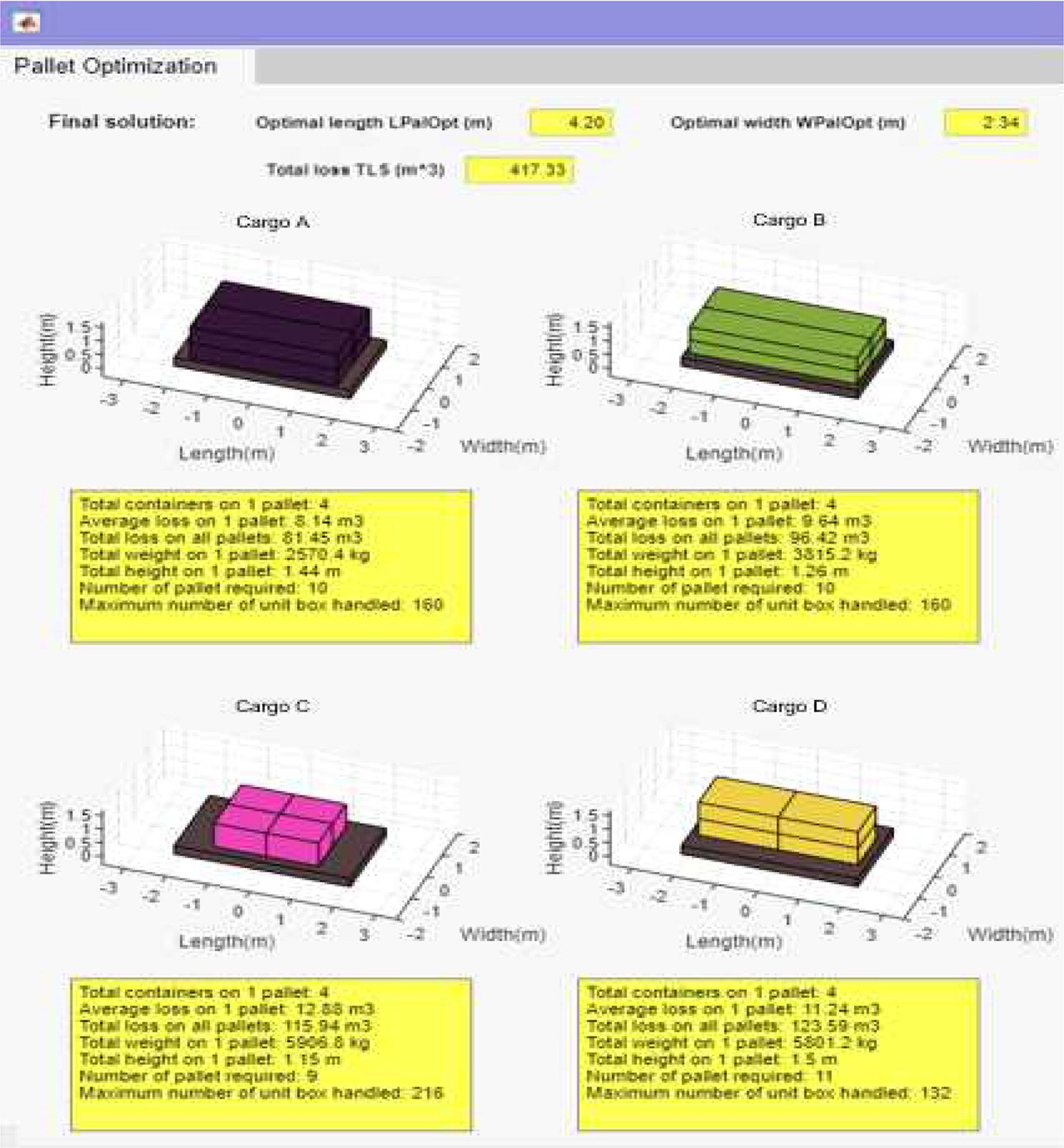
The optimal pallet size information includes the optimal pallet length and width calculated by the optimization module. The stackable quantity information is calculated by the quantity of cargo or containers that can be loaded on a single pallet when applying the optimal pallet size, as well as the number of pallets required to load all quantities of cargo. In addition, the stacking method is visualized as a 3D model, and the single pallet loss space and total loss space are finally calculated.
Output interface of the optimization module
Output features of the optimization algorithm
4.3 Optimality Verification
The proposed pallet size optimization algorithm was then verified by performing simulation analyses on randomly set special cargo. Four types of cargo (A, B, C, and D) were constructed with arbitrarily set dimensions, weights, heights, and storage quantities. Among them, the storage quantities for each type were limited to a total of 600, taking into account the limited storage space.
Specifications of the special cargo used in the simulation
Input features regarding the constraints used in the simulation
As mentioned in the previous section, the optimization algorithm in this study was designed to continue the search by expanding the range corresponding to the neighboring solutions if the objective function value of the neighboring solution is greater than or equal to the current solution instead of terminating the search. This was done by setting the search expansion coefficient δ.
Furthermore, to confirm whether the final global optimal solution was derived without being trapped in a local optimal solution during the search process, simulation was repeated by setting five different initial pallet sizes.
Initial pallet size for each cases
4.4 Simulation Result
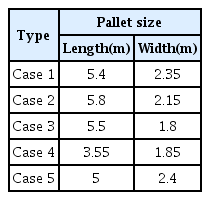
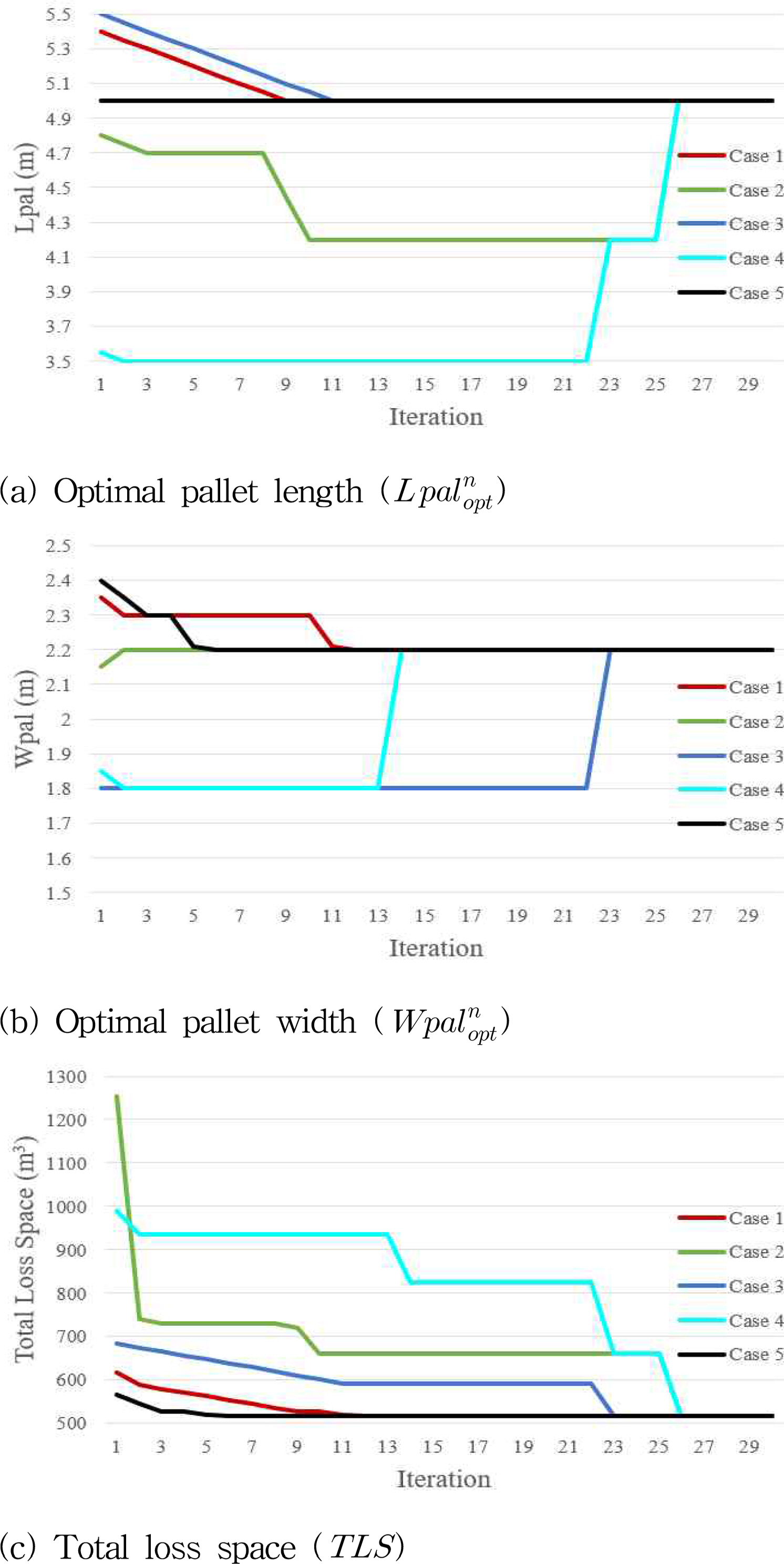
The simulation was repeatedly done with five different pallet sizes, and the optimal pallet size with the total loss space for each iterations were plotted in Fig. 7. The number of iterations required to reach the optimal solution varied for each case (12 for Case 1, 26 for Case 2, 23 for Case 3, 26 for Case 4, and 6 for Case 5), but all five cases resulted in the same optimal pallet size (length: 5m, width: 2.2m).
Simulation result of each cases
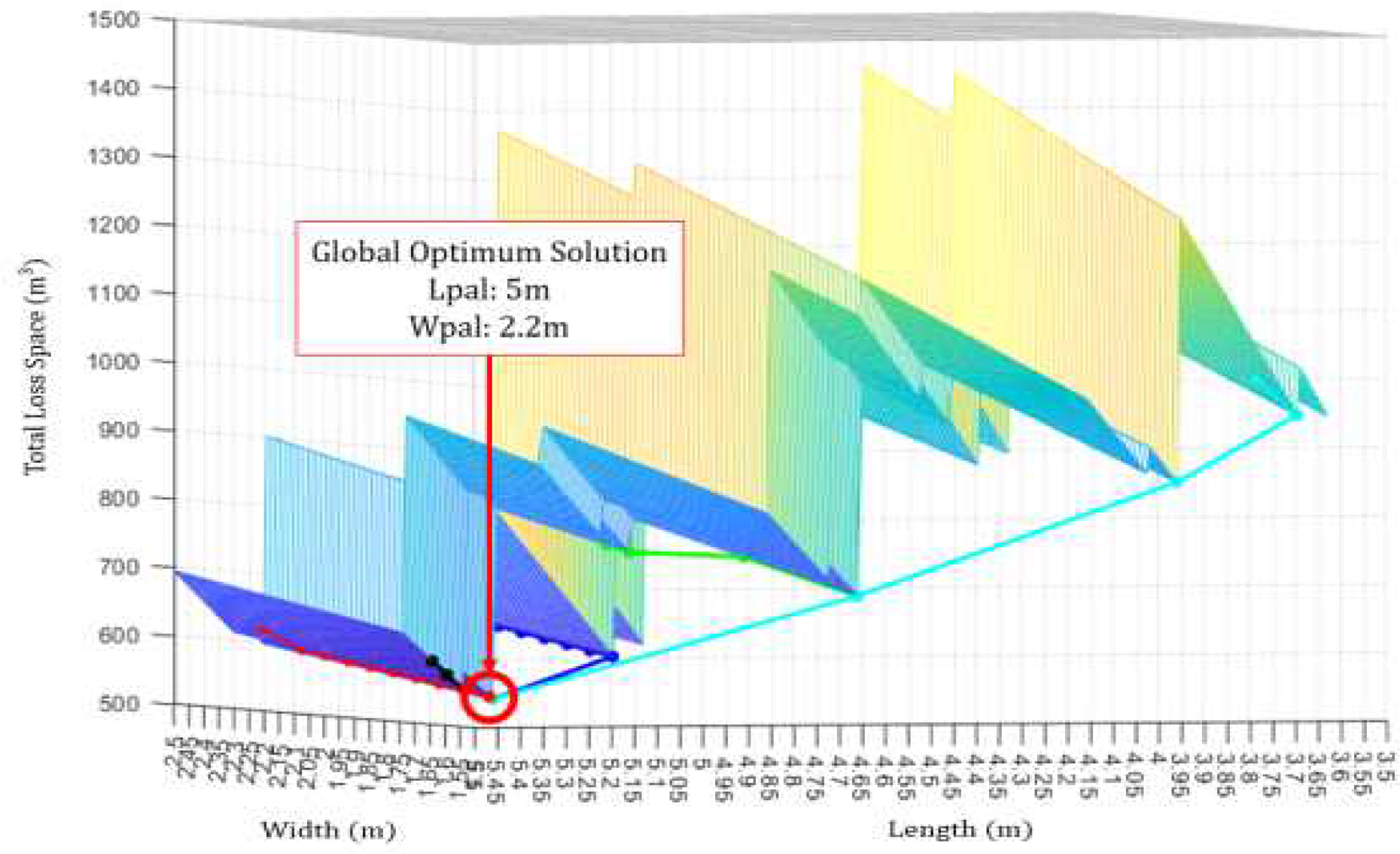
In addition, in order to confirm whether the optimal pallet size is found by the proposed optimization algorithm within the allowable range, the search process of pallet size for each cases were plotted in a 3D graph.
As shown in Fig. 8, when the pallet length is 5m and the width is 2.2m, the total pallet loss is minimized (515.32 ㎥), confirming that the optimal pallet size of the module is the global optimum solution. It was also shows that regardless of the initial palette size, the search process does not settle for a local optimum solution.
3D Visualization of the pallet size optimization result
5. Conclusion
In this study, we defined the pallet size optimization problem to minimize the loss space of pallets that load multiple special goods. We proposed an algorithm to search for the global optimal solution by modifying the traditional hill-climbing search.
The algorithm is designed to output the optimal pallet size information, stackable quantity information, and pallet loss space information based on the specifications and storage quantity of each type of goods, as well as constraint-related information. In order to search for the global optimal solution, we modified the method of hill-climbing search by extending the search range.
Furthermore, simulation analysis was performed on arbitrary special goods, and the optimality of the algorithm was verified by confirming that it ultimately derived the global optimal solution without terminating during the search process.
Therefore, it is expected that the developed algorithm in this study can improve space utilization and reduce time and cost by minimizing total loss space that occurs when handling multiple special goods. With optimized pallet sizes, companies can design efficient storage systems, plan effective picking and packing operations, and optimize warehouse layout and flow. This streamlines material flow, reduces handling time, and improves overall operational productivity. Also, such optimization algorithm could contribute to better inventory management. By selecting the right pallet size, companies can organize and track inventory more efficiently. This enables faster inventory replenishment, accurate stock counting, and improved visibility of available goods. Effective inventory management leads to reduced stockouts, better demand forecasting, and improved customer service levels.
For future work, since the simulation of this study has been done based on random set value, the verification is required based on actual cases of handling special cargo. Additionally, in order to prove that the proposed algorithm could be applied regardless of the searching range for, it would be necessary to review the searching process when the allowable range of pallet size is expanded.
Acknowledgements
This research was supported by the Defense Rapid Acquisition Technology Research Institute, Korea (UC200008D)