선박의 동적위치유지 시스템을 위한 Sliding Mode 제어 연구
A Study on a Sliding Mode Control Algorithm for Dynamic Positioning System of a Vessel
Article information
Abstract
본 연구에서는 선박 또는 해양구조물에 설치되는 터렛(Turret)과 같이 제어 대상의 무게 중심 주변이 아닌 임의 지점을 운동 중심으로 선정하여 제어할 수 있는 동적위치유지(Dynamic positioning; DP)용 슬라이딩모드(Sliding mode) 제어기를 연구하였다. 이러한 슬라이딩모드 제어기는 선박 및 해양구조물 동역학 모델의 불확실성, 시공간에서 변화하는 미지의 해양환경에 의한 외력, DP 제어시스템의 과도 성능을 고려한 제어가 가능하다. 선박 및 해양구조물의 임의 지점을 기준으로 제어하기 위해 제어 대상의 기구학 방정식에 포함되는 자코비안(Jacobian) 행렬을 수정하여 슬라이딩모드 제어기를 설계하였다. 제어기의 강건성(Robustness)을 확보하기 위해 슬라이딩모드 제어기 설계에리아프노프(Lyapunov) 안정도 판별 이론을 적용하였다. 일반적으로 DP 제어에서 제어기의 강건성 확보를 위해 PD(Proportional derivative) 제어 알고리즘 기반의 이득 스케줄링(Gain scheduling)을 사용한다. 그러나 이득 스케줄링을 적용하기 위한 적절한 이득을 찾는 것은 DP 시스템 적용을 복잡하게 만든다. 따라서 본 연구에서는 이러한 선박 및 해양구조물 DP 제어기의 복잡성을 해소하기 위해 슬라이딩모드 제어 알고리즘을고려하였다. 제안된 슬라이딩모드 제어 알고리즘의 유효성을 검증하기 위해 시간 영역 시뮬레이션을 구현하였으며, 제어 알고리즘의 성능평가에활용되었다. 제안된 슬라이딩모드 제어기의 유효성 검토를 위해 일반적인 PD 제어 알고리즘을 적용한 DP 제어 시뮬레이션 결과와 비교하였다.
Trans Abstract
In this study, a sliding mode (SM) controller for dynamic positioning (DP) was specifically designed for a turret connection operation of a ship or an offshore structure in which an arbitrary point on the structure could be controlled as the motion center instead of the center of mass. The SM controller allows control of the arbitrary point and provides capability to manage uncertainties in the dynamics of ships and offshore structures, external forces caused by unknown changing marine environments, and transient performance of DP systems. The Jacobian matrix included in kinematic equations of the controlled object was modified to design the SM controller to control based on an arbitrary point of ships or offshore structures. To ensure robustness of the controller, the Lyapunov stability theory was applied in the design of the SM controller. In general, for robustness in DP control, gain scheduling based on a proportional-derivative (PD) control algorithm is employed. However, finding appropriate gains for gain scheduling complicates the application of DP systems. Therefore, in this study, the SM control algorithm was considered to mitigate the complexity of the DP controller for ships and offshore structures. To validate the proposed SM control algorithm, time-domain simulations were conducted and utilized to evaluate the performance of the control algorithm. The effectiveness of the proposed SM controller was assessed by comparing simulation results with results of a conventional PD control algorithm applied in DP control.
1. 서 론
최근 인류의 생산 활동 범위가 수천 미터 이상의 깊은 해양과 극지(Arctic and Antarctic region)까지 다양한 공간으로 확대되는 상황에서 진보된 해양기전(Marine mechatronics) 시스템에 대한 요구가 높아지고 있다. 대표적인 해양기전 시스템 중 하나인 동적위치유지(Dynamic positioning; DP) 시스템은 해양구조물 또는 선박이 다수의 추진시스템을 활용하여 해양에서 시간의 흐름에 따라 변화하는 외력을 극복하고 자신의 위치를 유지하거나 정해진 경로를 따라 운항하도록 제어하는 시스템이다. DP 시스템을 탑재한 해양 시스템은 깊은 바다나 적은 매장량을 갖는 소규모 해양 유전 개발에서 많이 활용된다. 이는 DP 시스템이 전통적인 해양구조물의 위치 유지 방법인 계류 시스템(Mooring system) 또는 자켓 구조물(Jaket structure)을 사용하는 것보다 이러한 환경에서 경제적, 기술적으로 유리하기 때문이다. 또한 DP 시스템은 해양 시추(Marine drilling), 준설(Dredging), 구조물 승하강(Lifting), 파이프 설치(Pipelaying), 해중 구조물 설치 및 유지보수(Subsea installation and maintenance), 해양구조물 간 작업인력 운송(Passenger cruises), 해양 조사(Oceanographic research), 해상 로켓 발사(Rocket launch) 등의 다양하면서 새로운 해양 작업에서 활용되고 있는 상황으로 미래 해양산업의 필수 요소로 자리 잡아 가고 있다(Fossen, 2011; Shi et al., 2017).
해양에서 다양한 목적으로 사용되는 DP 시스템의 효과적인 운용을 위해서는 시스템의 적절한 제어 성능 확보가 필수적이다. 1960년대 초 DP 시스템이 처음 개발되었을 때 전후동요(Surge), 좌우동요(Sway), 선수동요(Yaw)를 독립적으로 제어하는 SISO(Single input single output) 구조의 비례-미분(Proportional derivative; PD) 제어기가 저주파수 통과 필터(Low-pass filter)와 함께 적용되었다(Steinbeck, J., 1961). 그 이후 다양한 DP 시스템 제어기법들이 연구되어오고 있다. Balchen et al.(1976)과 Grimble et al.(1979) 등은 DP 시스템에 다변수 최적 제어(Multivariable optimal control) 기법과 칼만 필터(Kalman filter)를 적용하는 연구를 성공적으로 수행하였다. 이는 오늘날까지 DP 시스템이 해양의 많은 분야에서 활용될 수 있도록 하는 시스템 신뢰성과 안정성을 확보하는 토대가 되었다. Fossen et al.(2001)과 Kim et al.(2015)은 비선형 제어(Nonlinear control) 이론을 적용하여 선박에 작용하는 주 외력 방향으로 해양구조물 또는 선박의 선수각(Yaw angle)을 자동으로 조정하여 최소의 해양환경 외력이 작용하는 조건을 만들어 사용 에너지를 최소화하는 웨더베닝(Weathervaning) 제어 알고리즘을 개발한 바 있다. Kim et al.(2017)은 더 나아가 직렬배치(Tandem arrangement)된 FPSO(Floating production, storage, and offloading)와 셔틀탱커(Shuttle tanker)의 적하역 작업에 웨더베닝 제어기법을 적용하여 효과적인 DP 시스템의 다수 부유체 간 적하역 작업 활용 가능성을 보였다. 이외에도 최근까지 이루어진 다양한 DP 제어기법에 대한 소개는 Sørensen(2011)을 참조하기 바란다.
국내에서도 다수의 DP 제어 연구가 이루어지고 있다. Lee et al.(1988)은 칼만필터와 LQG(Linear quadratic Gaussian) 제어기를 적용하여 반잠수식 해양구조물의 DP 제어 시뮬레이션을 수행하였다. Yoo et al.(1996)은 H∞제어기법을 DP 제어에 적용하였고 시뮬레이션을 통해 LQG 제어기와의 성능을 비교하였다. Lee et al.(2003)은 최적 제어 이론인 LQR(Linear quadratic regulator)과 LQI(Linear quadratic regulator with error integrator)를 DP 제어에 적용하였다. 또한 Kim et al.(2013)은 셔틀탱커 DP 제어시스템에 적분(Integral) 제어기의 발산 성향을 억제하는 안티 와인드업(Anti windup) 제어기를 포함하는 비례-적분-미분(Proportional integral derivative; PID) 제어기를 적용하여 모형시험과 시뮬레이션을 통해 그 유효성을 보였다. 또한 Jeon et al.(2017)은 퍼지시스템을 적용한 DP 시스템용 PID 이득 스케줄링(Gain scheduling)을 연구한 바 있다.
최근 해양 작업의 종류와 실행 빈도가 증가함에 따라 다양한 선종 및 작업 시나리오에 적용이 가능한 강건한 DP 제어기법에 관한 연구가 필요하다. 이를 위해 선박의 수학 모델, 센서 측정과 지속적인 해양환경 변화 및 선박 상태 변화에 강인한 슬라이딩모드(Sliding mode; SM) 제어기가 고려되고 있다. Tannuri 연구팀은 터렛 계류된 FPSO의 선수동요 제어를 위해 SM 제어기를 적용하였고, 전후동요, 좌우동요, 선수동요 방향의 수평면 3 자유도(3 degrees of freedom) 운동을 동시에 제어하도록 확장하였다(Tannuri et al., 2001, 2010). 국내에서는 Lee et al.(2005)이 SM 제어기로 컨테이너의 흔들림을 제어하며 정해진 이송궤적을 추종하는 크레인 제어기법을 연구하였다. Kim(2006)은 무인잠수정의 심도 및 평면 조종제어에 SM 제어를 적용하여 시뮬레이션을 통해 그 유효성을 보인 바 있다. Kim et al.(2011)은 Manta 형 UUV (Unmaned underwater vehicles)의 자유항주 실험에서 잠수정 제어에 SM 제어기를 적용한 바 있다. 선박 제어와 관련해서는 Xu et al.(2018)가 주어진 경로점들(Way points)을 추종하는 선박의 조종을 위해 SM 제어기를 적용한 바 있다.
본 논문에서는 선박 또는 해양구조물의 터렛(Turret) 접속 작업에 활용이 가능한 DP 제어기로서 SM 제어기를 적용하였다. 일점계류(Single point mooring) 방식인 터렛 접속을 위해서는 터렛 접속부가 해양구조물의 중심부에 위치하지 않을 때가 있으므로 구조물의 임의 지점을 회전 중심으로 하면서 이 회전 중심이 터렛 접속 완료가 될 때까지 정해진 위치를 유지하는 DP 제어 알고리즘이 필요하다. 제어 대상의 임의 지점을 제어하기 위해 기구학 방정식에 포함되는 자코비안(Jacobian) 행렬을 수정하여 제어기를 설계하였다. 일반적으로 DP 시스템용 PD 제어기의 경우 성능 확보를 위해 환경 외력 변화에 대하여 그 특성에 맞는 이득(Gain)을 직접 조정하거나 다층의 이득을 미리 설정해 놓고 상태 및 환경에 맞추어 자동으로 이득을 조정하는 이득 스케줄링(Gain scheduling)을 사용한다. 그러나 이러한 이득 스케줄링은 시스템의 복잡성과 적정 이득 조정의 어려움을 가져오며, 때때로 DP 시스템과 같은 비선형 플랜트 제어에서 만족스럽지 못한 성능을 보이기도 한다. 이에 본 연구에서는 비선형 제어기법의 하나인 SM 제어기를 DP 시스템 제어에 활용하여 해양환경에서의 외란에 강인한 DP 성능을 확보하고자 한다. 아울러 제어 대상 선박의 응답 특성을 직관적으로 고려하는 제어 파라미터 선정을 통한 제어 성능 확보에 대하여 검토하였다. 또한 선박 및 해양구조물의 운동을 수치적으로 모사할 수 있는 MATLAB/ Simulink 기반의 시뮬레이터를 구성하여 제안하는 제어 알고리즘의 유효성을 평가하였다. SM 제어기 설계를 위해 미지의 외력 항을 포함하는 간략화된 운동방정식이 활용되었고, 제어기의 강인성(Robustness)을 확보하기 위해 리아프노프(Lyapunov) 안정도 판별 이론을 적용하여 SM 제어기를 설계하였다. 설계된 제어기는 시간영역(Time domain) 시뮬레이션을 통해 평가되었고 일반적인 PD 제어기 적용 결과와 비교하여 유효성 및 우수성을 검토하였다.
본 논문에서는 DP 시스템 성능평가를 위한 시뮬레이터 구성과 이에 활용된 선박 운동 이론을 2장에 정리하였다. 선박의 특정 위치를 중심으로 DP 제어가 가능하게 하는 SM 제어기 설계는 3장에서 소개한다. 해양환경 조건에서의 DP 제어 시뮬레이션 결과를 4장에서 보이며, 마지막 5장에서는 연구내용을 요약 및 정리하여 결론을 제시한다.
2. DP 제어 검증을 위한 시뮬레이터 및 수학 모델
본 장에서는 DP 제어 성능평가를 위한 시뮬레이터와 선박 운동 모델, 센서 모델, 필터 모델을 소개한다. DP 시스템을 탑재한 선박의 운동 및 제어 응답을 평가하기 위해 전후동요, 좌우동요, 선수동요의 수평면 3 자유도 운동을 모사하는 해양구조물 시뮬레이터가 Matlab/Simulink 기반으로 개발되었다. 해당 시뮬레이터는 선박의 운동을 계산하는 선박 모듈(Vessel module)과, 측정되는 센서 신호를 모사하는 센서 모듈(Sensor module), 제어를 위해 제거되어야 하는 신호를 분리하는 필터 모듈(Wave Filter module), 그리고 대상 구조물의 상태로부터 제어력을 계산하는 제어기 모듈 (Controller module)로 구성된다. 본 시뮬레이터의 GUI (Graphical user interface)를 Fig. 1에 보이고 있다 (The Math Works, Inc., 2022).
해양 외력인 파력(Wave forces), 조류력(Current force), 해상풍력(Wind force)의 영향을 고려하여 해양구조물 또는 선박의 운동 응답을 계산하는 수학 모델을 본 장에서 소개하고자 한다. 해양에서 운항하는 선박은 6 자유도(6 degrees of freedom) 운동을 하게 되며, 이는 3 자유도의 직선 운동인 전후동요, 좌우동요, 상하동요(Heave)와 3 자유도 회전운동인 횡동요(Roll), 종동요(Pitch), 선수동요이다. 그러나 본 연구의 대상이 되는 DP 시스템은 3 자유도 수평면 운동 즉, 전후동요, 좌우동요, 선수동요만을 고려하므로 본 장에서 3 자유도 수평면 운동 모델을 소개한다.
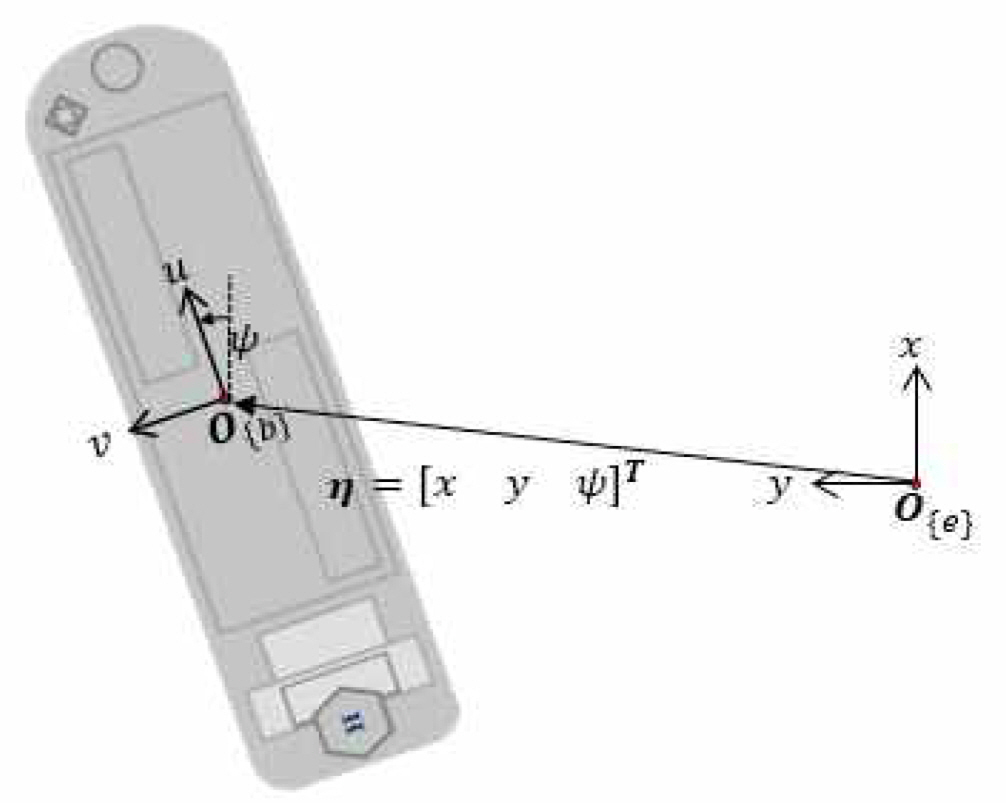
선박의 운동은 식 (1)과 같이 표현되며, η는 Fig. 2에 보이는 바와 같이 지구고정좌표계 {e}에서 정의되는 선박의 위치(x,y)와 선수각(ψ)을 나타내는 상태 변수 벡터이다. 선박의 운동방정식을 기술하기 위한 좌표계를 Fig. 2에 보이고 있다. 선박의 운동은 파랑 표류력(Wave drift force), 조류력, 해상풍력의 영향으로 나타나는 저주파수 운동 ηL과 파랑 기진력(Wave exciting force)에 의해 나타나는 고주파수 (또는 파주파수) 운동 ηH로 구성된다.
선박의 운동방정식 중 기구학식은 식 (2)로 표현되며, 지구고정좌표계 {e}와 물체고정좌표계 {b} 사이의 운동 변환을 나타낸다. 여기서 ν는 물체고정좌표계에서 정의되는 선박의 운동 속도로 u,v,r은 각각 전후동요, 좌우동요, 선수동요의 속도이다. R(ψL)은 물체고정좌표계 {b}의 속도를 지구고정좌표계 {e}의 속도로 변환하는 오일러 각 변환 행렬(Euler angle transformation matrix)이다.
선박의 운동방정식 중 동역학식은 식 (3)과 같이 표현할 수 있다. M0는 선박의 관성 행렬로서 선체 질량과 선체 주변 유체에 의해 나타나는 부가질량(Added mass) 중 저주파수에서의 부가질량의 합이다. 일반적으로
수선면 위로 드러난 구조물은 형상에 따라 해상풍 하중을 받게 되며, 이는 아래 식 (4)와 같이 표현된다. 여기서 τwind는 선박에 작용하는 해상풍력을 나타내는 해상풍력 벡터이고, ρa는 공기의 밀도이다. Uw는 해상풍 속도로
선박에 작용하는 파랑 표류력 τwave는 2차 비선형 전달 함수(Quadratic transfer functions; QTF)를 활용하여 식 (5)와 같이 표현된다. 운동 방향마다 파랑 표류력이 계산되어야 하며 식 (5)에서는 전후동요, 좌우동요, 선수동요 방향을 -방향 파랑 표류력을 표현하였다. 여기서 Aj와 Ak는 해양파(Wave)를 구성하는 N개의 파주파수 성분 중 j번째 및 k번째 파주파수의 진폭(Amplitude)을 의미하며, 이 진폭은 주어지는 파스펙트럼(Wave spectrum)으로부터 불규칙파(Irregular wave)를 생성할 때 계산된다. 비선형 전달함수는 고차경계요소법(High-order boundary element method) 등을 활용한 수치해석 프로그램을 통해 계산되는 파랑 표류력을 표현하는 복소함수이며,
고주파수 운동 ηH는 식 (6)과 같이 고차경계요소법 등을 활용하는 수치해석 프로그램을 통해 계산할 수 있는 선형 전달 함수(Linear transfer function)인 RAO(Response amplitude operator)를 이용하여 표현할 수 있다. 여기서 RAO 역시 복소함수로 표현되며,
DP 제어 응답 평가를 위한 수평면 3자유도 선박 운항 시뮬레이터의 센서 오차 신호를 모사하는 Fig. 1의 센서 모듈에 사용된 노이즈 생성은 식 (7)의 1차 Gauss-Markov process를 활용하였다. 여기서 yi는 측정 물리량, w는 가우시안(Gaussian) 백색 잡음(White noise), μ ≥ 0는 물리량 계측 센서의 장주기 오차를 만들어내는 시정수(Time constant)의 역수이다.
또한 시뮬레이터에는 선박의 저주파수 운동, 파주파수 운동 및 센서 노이즈로 구성된 선박 운동 계측 정보로부터 저주파수 운동을 분리해 내고, 선박의 운동을 만들어낸 해양환경 외력을 추정하는 확장 칼만 필터(Extended Kalman filter)를 구성하여 적용하였다. 아울러 선박 모델에 포함된 추진시스템 모델은 각 추진기 특성의 최대 변화 속도가 제한되는 1차 미분 방정식 모델로 구성하였다. 또한 제어기에서 계산된 3 자유도 제어력을 다수의 추진기로 분배하는 추력 분배 알고리즘 역시 라그랑지 승수(Lagrange multiplier) 이론을 기초로 구성하여 적용하였다. 본 문단에서 언급된 확장 칼만 필터, 추진시스템 모델, 추력 분배 알고리즘은 본 논문에서 논하지 않으므로 자세한 설명은 Fossen(2011), Sørensen(2012), Kim(2018)을 참조하기 바란다.
3. Sliding Mode 제어기 설계
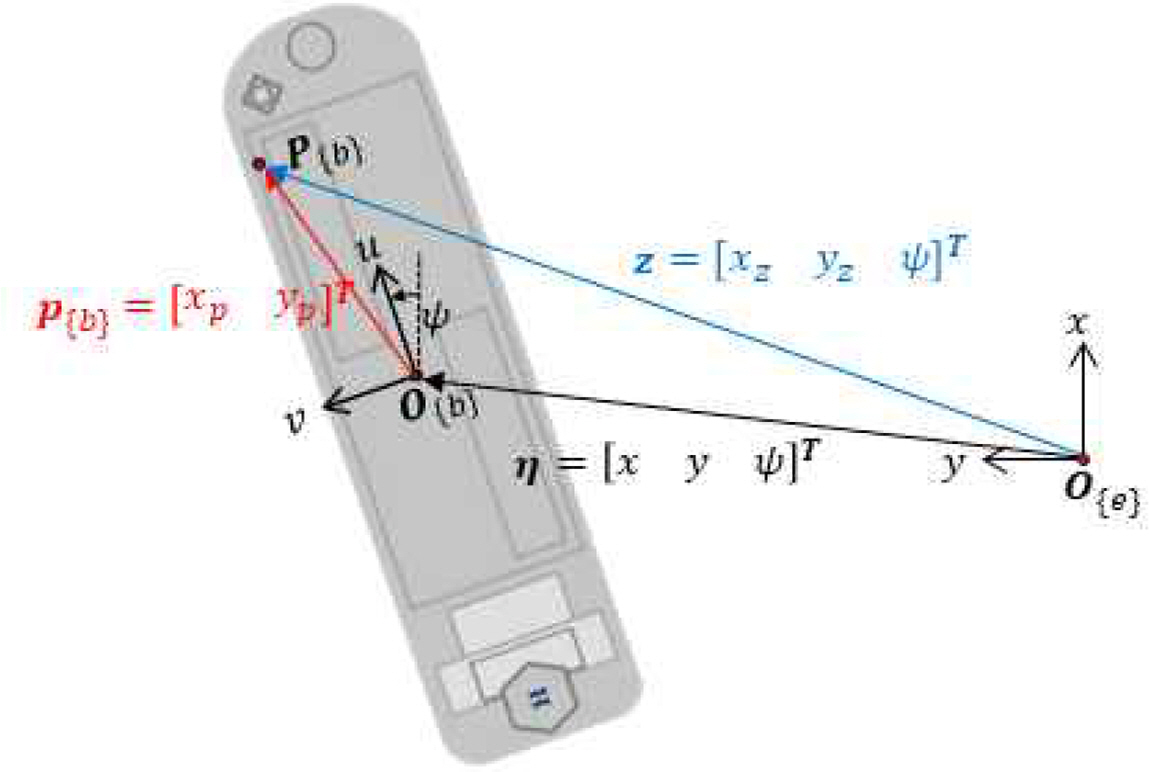
본 장에서는 터렛 접속 작업을 수행하는 FPSO의 터렛 접속부 위치를 제어하기 위한 SM 제어기 설계를 소개한다. Fig. 3에 보이는 바와 같이 접속 작업을 수행할 터렛 접속부(P{b})는 FPSO의 선수부 임의 위치에 있다고 가정하였다. 선수부에 위치하는 특정 지점(z)을 목표 지점zd에 고정되도록 제어를 수행해야 하므로 선박의 운동을 변환하기 위한 기구학식을 식 (8)과 같이 구성하였다. 물체고정좌표계 {b}에서 정의되는 터렛 접속부의 위치를
본 논문에서 다루는 제어 목표는 선수부 터렛 접속부의 위치를 특정 지점에 고정하고, 선박의 운동 속도가 0이 되도록 하는 것이며 이를 식 (11)과 같이 표현할 수 있다.
상기 언급된 제어 목표를 달성하기 위해 먼저 제어 대상 오차를 식 (12)와 같이 정의하고, SM 제어를 위한 슬라이딩 평면(Sliding surface)을 식 (13)과 같이 정의한다. 여기서 Iλ는 시스템 상태가 슬라이딩 평면에 올랐을 때 되먹임 제어(Feedback control)를 위한 이득으로 모든 요소가 양의 값을 가져야 하며, 따라서 s=0의 조건을 충족할 때 시스템 오차 e가 자동으로 0으로 수렴하게 된다.
강인 제어기 설계를 위해 제어시스템의 리아프노프 함수(Lyapunov candidate function)를 슬라이딩 평면 변수를 활용하여 식 (14)와 같이 선정하고, 제어시스템의 안정성을 판별하기 위해 해당 리아프노프 함수의 미분을 취하면 식 (15)와 같이 정리된다.
SM 제어기 u는 되먹임(Feedback) 제어기 uf와 스위칭(Switching) 제어기 us로 구성한다. 우선 되먹임 제어기 uj를 식 (16)과 같이 선택하고 리아프노프 함수의 미분식에 대입하면 식 (17)을 얻게 된다. 여기서
마지막으로 스위칭 제어기 us를 식 (18)과 같이 선택한다. 여기서 F는 미지의 외력 w과 외력 추정값
식 (18)과 같이 선택된 스위칭 제어기 us를 식 (17)에 대입하면 식 (19)와 같이 유도된다. 선박의 질량 행렬은 상수 행렬로 M=MT>0이며, M-1>0이다. 또한 수치해석을 통해 {-π ≤ ψ ≤ π}조건에서 JM-1>0이 성립함을 확인하였다. 따라서
4. 수치시뮬레이션
본 장에서는 SM 제어기를 적용한 FPSO의 DP 시뮬레이션 내용과 결과를 소개하고 SM 제어기의 특성 및 유효성을 논의한다.
4.1 수치시뮬레이션 구성
SM 제어기를 구현하기 위해서는 동역학 시스템 모델 및 외력의 불확실성 추정이 필요하며, 되먹임 제어기 식 (16)과 스위칭 제어기 식 (18)에서 보이는 바와 같이
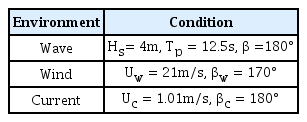
본 연구에서는 해양에서 터렛 접속 작업을 수행하는 FPSO를 가정하고, SM 제어기를 적용하여 그 유효성을 평가한다. 대상으로 하는 FPSO는 300m급으로 Table 1에 주요 제원 및 물리적 파라미터들을 정리하였다. 또한 FPSO의 DP 제어를 위해 최대 추력 500kN 생성이 가능한 아지머스(Azimuth) 추진기 6기가 설치되어 있다고 가정하였고, 추진기의 종류, 설치 위치 및 용량 정보를 Table 2에 정리하였다. 시뮬레이션을 위해 선정된 해양환경 조건은 Table 3에 정리하였다. 본 연구에서 선정한 해양환경 조건은 터렛 접속 작업의 한계 조건(operation limit)을 가정하여 결정하였다.
SM 제어기의 제어 변수로는 시스템이 슬라이딩 평면에 도달했을 때 작용하는 되먹임 제어 이득 Iλ, 스위칭 제어 이득 F와 β0, 그리고 채터링 감소를 위한 슬라이딩 평면 경계 변수 ϵ가 있다. 본 연구에서는 Tanurri et al. (2010)가 제안한 SM 제어 변수 설정법을 고려하여 제어 변수를 Table 4와 같이 설정하였다. 여기서 treach는 슬라이딩 변수가 슬라이딩 평면 경계 밖에 위치할 때 다시 경계 안으로 들어오는 시간을 의미하며, 본 연구에서는 30s로 설정하였다. 또한 emax는 전후동요, 좌우동요, 선수동요의 최대 허용 오차를 의미하며, 각각 ±2m, ±2m, ±1°로 설정하였다.
4.2 수치시뮬레이션 결과 및 토의
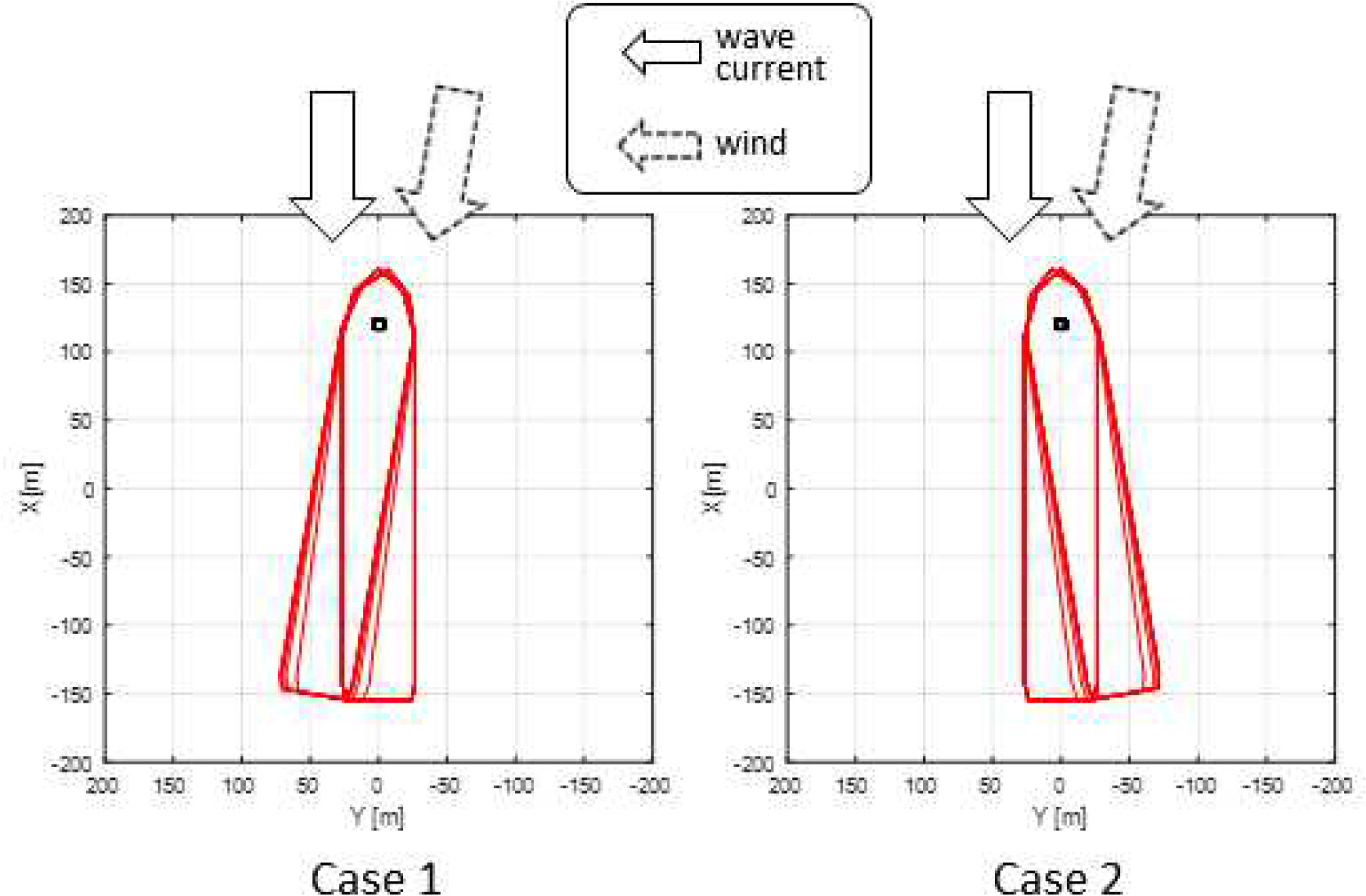
터렛 접속 작업을 수행하는 FPSO의 위치를 동적으로 제어하기 위해 설계된 SM 제어기의 성능평가를 위해 Table 5에 보이는 두 가지 제어 시나리오를 고려하였다. 첫 번째 시나리오 Case 1은 선박에 설치된 터렛이 접속 작업을 수행하기 위한 위치에 도달하였다고 가정하고, 초기에는 파랑과 조류의 입사각에 대하여 선체가 평행하게 유지하는 선수각 0°를 유지하다가 나중에 해상풍의 입사각과 선체가 평행을 유지하도록 선수각을 -10°로 변환하는 조건이다. 두 번째 시나리오 Case 2는 Case 1과 동일한 초기 제어를 수행하다가 선수각을 10°로 변환하여 어떤 환경 외력과도 평행을 이루지 않는 조건이다. 따라서 Case 1보다 Case 2가 선체에 상대적으로 더 큰 환경 외력이 작용하는 조건임을 알 수 있다. 제어 시나리오의 이해를 돕기 위해 Fig. 5에 선박의 운동을 환경 외력 작용 방향과 함께 도시하였다.
DP를 위해 설계된 SM 제어기와 성능 비교를 위해 일반적인 PD 제어기를 설계하여 적용하였다. 두 제어기의 성능 비교를 위해 초기 제어 시간 1,000s에서 2,500s까지 1,500s 동안 사용된 제어력의 절댓값 합(=Σ|u|)이 서로 비슷하도록 PD 제어기 이득(Gain)을 조정하였고, 각 제어 시나리오에서의 변화를 비교하였다. 시뮬레이션에서 사용된 PD 제어기 이득을 Table 6에 정리하였다.
SM 제어기와 PD 제어기를 적용한 FPSO가 Case 1 시나리오를 따라 제어된 시뮬레이션 결과를 Fig. 6에 함께 도시하였다. 해당 결과를 분석하는 데 있어 제어는 해양구조물의 무게 중심 위치를 기준으로 이루어진 것이 아니고 선수부에 위치한 터렛 접속부 위치를 기준으로 제어가 실행되었음을 기억하기 바란다. 따라서 분석에서의 운동과 오차는 터렛 접속부가 지구고정좌표계 {e}의 터렛 접속 작업 요구 위치에 고정되는 제어 상황을 고려하였음을 밝힌다. 시뮬레이션의 초기 1,000s는 파랑, 조류, 해상풍의 해양환경이 완전히 발전할 때까지의 구간으로 결과 분석에 포함하지 않는다.
SM 제어기 사용의 경우 시뮬레이션 시간 2,500s에서 선수각을 0°에서 -10°로 변경하는 제어 명령을 입력하였다. 이 계단 입력(Step input)에 따른 과도구간(Transient section)이 나타나고 오버슈트(Overshoot) 없이 3,000s 근방에서 시스템이 안정화됨을 Fig. 6 (b)에서 확인할 수 있으며, 이때 FPSO가 움직인 궤적(Footprint)을 Fig. 6 (a)에 표시하였다. 제어기에 입력된 제어 목표와 FPSO가 움직인 운동을 Fig. 6 (b)에 표시하였고, 이때 발생한 제어 오차를 Fig. 6 (c)에 보인다. 결과로부터 SM 제어기를 사용할 때 전후동요 방향은 제어 목표 120m를 중심으로 약 ±0.23m 이하의 오차를 보이며, 좌우동요의 경우 초기에는 제어 목표 0m를 중심으로 약 ±0.13m 이하의 오차를 보이다가 선수각 변경 후 -0.32m를 중심으로 ±0.17m 이하의 오차를 보인다. 선수각 오차는 계단 입력 직후에 최대 –8.84°의 오차를 가지며 점점 0°으로 수렴한다. Fig. 6 (d)는 슬라이딩 모드 제어기로부터 출력되는 제어력을 보이고 있으며, 선수각 변환 제어 명령에 의해 제어력이 급격히 증가하였다가 시스템의 선수각이 제어 목표에 수렴하면서 제어력이 서서히 감소함을 보이고 있다.
SM 제어기와 비교를 위해 설계된 PD 제어기를 적용한 FPSO가 Case 1 시나리오를 따라 제어된 시뮬레이션 결과 역시 Fig. 6에 같이 도시하였다. SM 제어기 시뮬레이션과 마찬가지로 2,500s에서 선수각을 0°에서 -10°로 변경하는 제어를 명령하였다. 이 계단 입력에 따른 과도구간이 나타나고 오버슈트를 거쳐 2,700s 근방에서 시스템이 안정화됨을 Fig. 6 (b)에서 볼 수 있다. 제어기에 입력된 제어 목표와 FPSO의 운동을 비교할 때 전후동요는 초기에 제어 목표 120m에 미치지 못하는 117.35m를 중심으로 약 ±0.34m 정도의 오차를 보이다가 선수각 변경 후 117.51m를 중심으로 약 ±0.38m 정도의 오차를 보인다. 좌우동요의 경우 초기에는 1m를 중심으로 약 ±0.12m 이하의 오차를 보이다가 선수각 변경 후 -0.4m를 중심으로 약 ±0.16m 이하의 오차를 보인다. 선수각은 계단 입력 직후에 -6.8°를 지나며 오버슈트 -10.6°를 거쳐 -10°근방으로 수렴한다. PD 제어에 의한 제어력 역시 선수각 변환 제어 명령에 의해 제어력이 급격히 증가하였다가 선수각이 제어 목표 근방으로 수렴하면서 제어력이 감소하는 현상을 보인다.
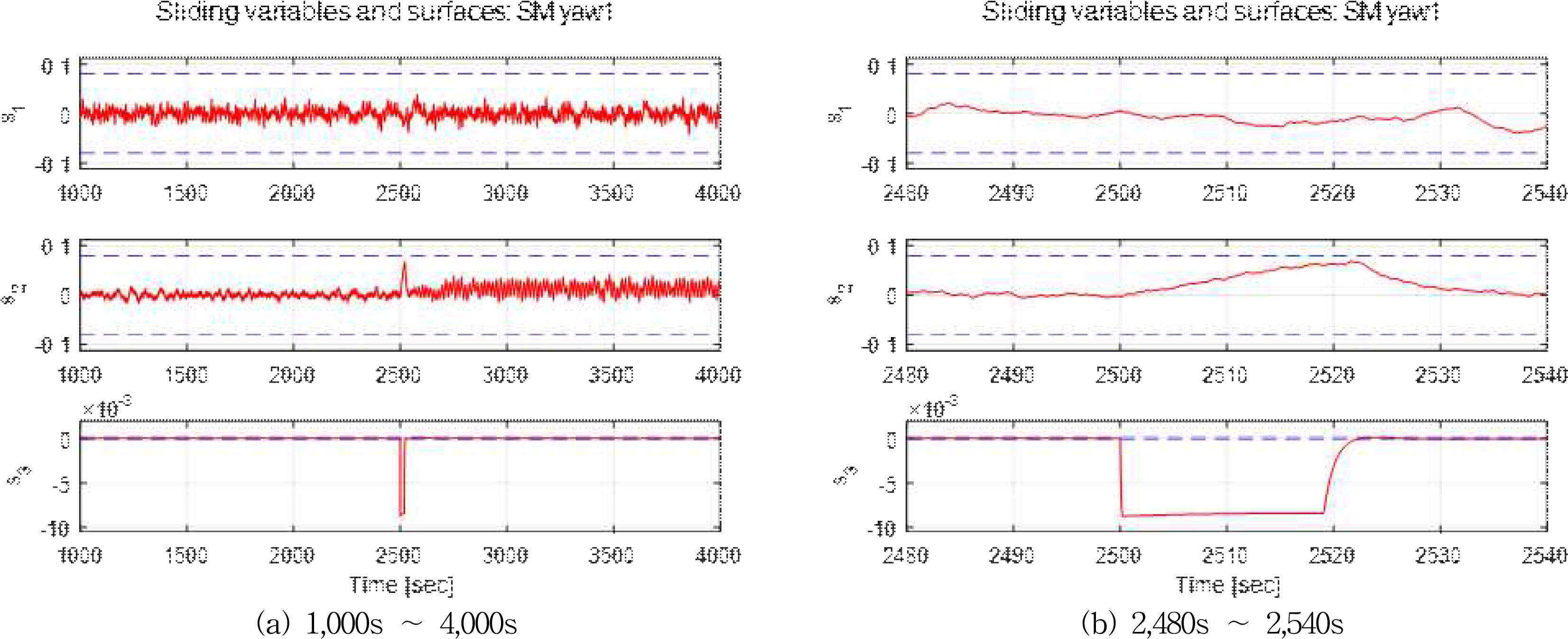
Fig. 7은 식 (13)에서 정의한 슬라이딩 모드 제어기의 슬라이딩 평면 응답을 보이고 있다. 여기서 s1, s2, s3는 각각 전후동요, 좌우동요, 선수동요 방향의 슬라이딩 변수를 나타내며, 점선은 슬라이딩 모드 제어기의 채터링 현상을 완화하기 위해 설정한 슬라이딩 평면 경계 변수 ϵ에 대응하는 값을 의미한다. 전후동요 및 좌우동요의 경우 슬라이딩 변수가 슬라이딩 평면 경계 내부에 위치하면서 s=0의 안정적인 슬라이딩 평면 응답을 보이고 있고, 선수동요의 경우 계단 입력이 시스템에 인가되었을 때 슬라이딩 변수가 슬라이딩 평면 경계 밖으로 이동했다가 일정한 시간 안에 슬라이딩 평면 경계 안으로 돌아오는 응답을 보이고 있다. Fig. 7 (a)와 (b)에서 보이는 바와 같이 선수각 변경 명령에 의한 계단 입력이 인가된 순간(시간 2500s) 선수동요 방향의 슬라이딩 변수는 슬라이딩 평면의 경계를 벗어나고 약 23s 후 다시 슬라이딩 평면 경계 안으로 돌아오는 것을 알 수 있다. 이는 Table 4에서 설정한 treach 즉 슬라이딩 변수의 슬라이딩 평면 경계 도달 시간 30s를 만족하는 결과이다. Fig. 8은 슬라이딩 변수 s를 구성하는 오차 e와 이 오차의 미분값
SM 제어기와 PD 제어기를 적용한 FPSO가 Case 1 시나리오를 따라 제어된 시뮬레이션 결과 비교를 위해 구간별 오차와 소요 제어력을 Table 7과 Table 8에 정리하였다. 구간은 선수각 제어 목표 변경 전을 ‘구간 1 (Duration I)’으로, 선수각 제어 목표 변경 후 시스템이 안정화된 영역을 ‘구간 2 (Duration II)’로 정의하였고, 제어 명령 입력에 의해 선수각의 급격한 변화가 나타나는 과도상태도 포함하는 전체 시뮬레이션 구간을 ‘구간 3 (Duration III)’으로 정의하였다. FPSO가 터렛 접속 작업을 수행하는 동안 소요한 제어력 비교를 위해 제어기로부터 산출되는 제어력의 절대값에 대한 합을 산출하였다.
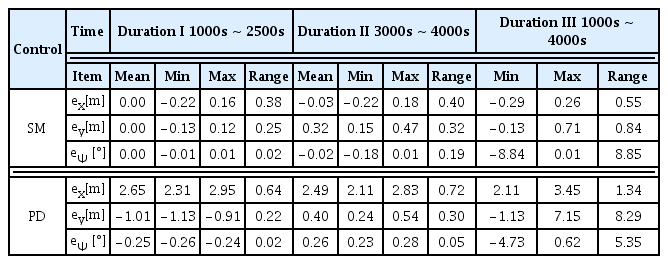
전후동요 방향의 경우 앞서 정의한 구간에 따른 오차 변화는 크지 않게 나타나고 있으나, 적용 제어기별 특성이 확연히 드러나고 있다. SM 제어기의 경우 구간 1에서 0.00m, 구간 2에서 –0.03m의 평균 오차을 보이고 있으나, PD 제어기의 경우 구간 1에서 2.65m, 구간 2에서 2.49m의 평균 오차를 보이고 있다. 이는 PD 제어기에 정상상태(Steady state) 오차를 제거하는 I(Integral) 제어기가 포함되지 않았기 때문에 발생하는 결과이다. DP 제어는 지속적으로 불규칙하게 진동하는 파랑기진력에 의한 환경 외력이 존재하므로 파랑기진력 성분을 완벽히 제거하는 필터링 기술을 사용하지 않을 때는 I 제어기를 사용하지 않고 정상상태 오차를 보상하기 위해 제어 목푯값을 다시 지정하여 운영하는 것이 일반적이다. 이와 비교하여 본 연구에서 제안하는 SM 제어기는 정상상태 오차를 제거하는 기능이 구조적으로 제어기에 포함되어 있어 큰 정상상태 오차가 없음을 확인할 수 있다. 과도상태를 포함하는 전체 시뮬레이션 구간인 구간 3에서의 오차는 SM 제어기의 경우 최대 오차 0.26m, 최소 오차 –0.29m가 관찰되었고, PD 제어기의 경우 최대 오차 3.45m, 최소 오차 2.11m가 나타났다. 오차의 변화 크기를 확인하기 위해 최대 오차(Max)에서 최소 오차(Min)를 뺀 오차 범위(Range)를 산출하였다. 그 결과 SM 제어기의 경우 오차 범위가 구간 1에서 0.38m, 구간 2에서 0.40m, 구간 3에서 0.55m가 나타났으며, PD 제어기의 경우 구간 1에서 0.64m, 구간 2에서 0.72m, 구간 3에서 1.34m가 관찰되었다. 이를 통해 SM제어기의 전후동요 오차 범위가 PD 제어기 대비 작음을 확인할 수 있다. 소요 제어력은 모든 구간에서 SM 제어기와 PD 제어기가 비슷한 제어력을 산출하고 있음을 확인할 수 있는데 구간 1보다 구간 2가 적은 제어력이 사용함을 알 수 있으며, 이는 해상풍과 평행하도록 FPSO가 선수각을 제어할 때 더 적은 환경 외력이 전후동요 방향으로 작용함을 의미한다.
좌우동요의 경우 구간에 따른 변화가 나타난다. SM 제어기는 구간 1에서 0.00m, 구간 2에서 0.32m 평균 오차를 보이고, PD 제어기는 구간 1에서 –1.01m, 구간 2에서 0.40m 평균 오차를 보이고 있다. 이는 전후동요 제어 결과와 마찬가지로 두 제어기의 정상상태 오차 제거 기능의 유무에 따른 특성으로 판단된다. 여기에 선수각 변화 과도상태를 포함하는 구간 3에서 SM 제어기의 오차 범위는 0.84m이고 PD 제어기의 오차범위는 8.29m로 큰 차이를 보인다. 이러한 결과로부터 PD 제어기를 사용할 경우 터렛 접속 작업시 터렛 접속부의 이탈이 상당히 크게 발생할 수 있음을 유추할 수 있다. 이는 SM 제어기는 선수각 제어를 수행함과 동시에 다른 운동 즉 전후동요 및 좌우동요와의 간섭을 고려하여 제어를 수행하는 MIMO(Multi input multi output) 시스템인 반면 PD 제어기는 모든 운동을 독립된 제어 요소로 고려하는 SISO(Single Input Single Output) 시스템이기 때문이다. Table 8로부터 좌우동요 제어를 위해 구간 1과 구간 2에 대하여 SM 제어기와 PD 제어기가 비슷한 소요 제어력을 사용하고 있음을 확인할 수 있다. 그러나 선수각 변화가 있는 과도 상태인 구간 3에서 PD 제어기의 경우 좌우동요 방향에서 다소 큰 오차가 발생하였고 이를 제어하기 위한 더 많은 소요 제어력이 사용되었다. 그 결과 SM 제어기는 구간 3에서 1.22E+07kN의 소요 제어력을 사용하였고, PD 제어기는 1.52E+07kN 사용한다. 이는 SM 제어기가 PD 제어기 대비 약 20%의 제어력을 더 적게 사용하였음을 의미한다.
마지막으로 선수동요의 경우 구간 1과 구간 2에서 SM 제어기는 정상상태 오차가 거의 없으나, PD 제어기는 구간 1에서 –0.25°, 구간 2에서 0.26°를 보인다. 그러나 구간 3에서의 최소 에러는 SM 제어기가 –8.84°, PD 제어기가 –4.73°를 보이고 있다. 이는 PD 제어기의 반응이 SM 제어기보다 빨라서 나타나는 현상으로 생각된다. 그러나 빠른 선수각 제어 응답성을 갖는 PD 제어기의 경우 선수각 응답에서 눈에 띄는 오버슈트(Overshoot)가 나타나고 있음을 Fig. 6 (b)에서 확인할 수 있으며, 이는 더 많은 제어력 소모를 유발할 수 있다. 소요 제어력을 비교해 보면 구간 1과 구간 2에서는 두 제어기가 비슷한 소요 제어력을 사용하는 반면에 선수각 제어 과도 상태를 포함하는 구간 3에서는 SM 제어기 4.96E+08kNm, PD 제어기 8.48E+08kNm를 보이고 있다. 앞서 언급한 빠른 응답성에 따른 과도한 제어력 사용의 현상으로 보여진다. 해당 결과로부터 약 42% 제어력 감소가 PD 제어기 대비 SM 제어기 사용 상태에서 나타나고 있음을 확인할 수 있다.
앞서 소개한 바와 같이 SM 제어기는 허용오차 를 설정하여 설계되었다. 전후동요, 좌우동요의 과도상태를 포함하는 구간 3의 오차를 보면 ±0.29m(전후동요), ±0.71m(좌우동요) 이내로 발생하고 있으며, 이는 설정된 emax 값 ±2m(전후동요), ±2m(좌우동요)를 만족한다. 그러나 선수동요의 경우 직접적인 계단 입력(0° → -10°)을 받았으므로 설정된 허용오차 emax 인 ±1°를 만족하지는 못한다. 이와 비교하여 PD 제어기의 구간 3에서의 오차를 살펴보면 전후동요 ±3.45m, 좌우동요 ±7.15m 이내의 오차가 발생하고 있다. 이를 근거로 제안된 SM 제어기가 터렛접속 작업에 더욱 적합한 DP 제어기라고 주장할 수 있다.
Case 2 시나리오를 따라 SM 제어기와 PD 제어기로 시뮬레이션 수행한 결과를 Fig. 9에 도시하였다. SM 제어기의 경우 시뮬레이션 시간 2,500s에서 선수각을 0°에서 10°로 변경하는 제어 명령을 입력하였다. 이 계단 입력에 따른 과도구간이 나타나고 오버슈트 없이 3,000s 근방에서 시스템이 안정화됨을 Fig. 9 (b)에서 확인할 수 있으며, 이때의 대상 FPSO 궤적을 Fig. 9 (a)에 표시하였다. 제어기에 입력된 제어 목표와 FPSO가 움직인 운동을 Fig. 9 (b)에 도시하였다. 시뮬레이션 중 발생한 제어 오차를 Fig. 9 (c)에 보였다. Fig. 9 (d)는 제어기로부터 출력되는 제어력을 보이고 있으며, 선수각 변환 명령에 의해 급격히 증가하였다가 선수각이 제어목표에 수렴하면서 감소하였다. 결과로부터 전후동요 방향은 초기에 제어 목표 120m를 중심으로 약 ±0.22m 이하의 오차를 보이다가 선수각 변경 후 120.38m를 중심으로 약 ±0.2m 이하의 오차를 보인다. 좌우동요의 경우 초기에는 제어 목표 0m를 중심으로 약 ±0.13m 이하의 오차를 보이다가 선수각 변경 후0.4m를 중심으로 약 ±0.2m 이하의 오차를 보인다. 선수각 오차는 계단 입력 직후에 최대 약 8.88°의 오차를 가지며 점점 0°로 수렴한다. 비교 대상인 PD 제어기를 결과 역시 Fig. 9에 같이 도시하였다. SM 제어기 시뮬레이션과 마찬가지로 2,500s에서 선수각을 0°에서 10°로 변경하는 제어를 명령하였다. 이 계단 입력에 따른 과도구간이 나타나고 2,700s 근방에서 시스템이 안정화됨을 Fig. 9 (b)에서 볼 수 있다. 제어기에 입력된 제어 목표와 FPSO의 운동을 볼 때 전후동요는 초기에 제어 목표 120m에 미치지 못하는 117.35m를 중심으로 약 ±0.34m 정도의 오차를 보이다가 선수각 변경 후 117.17m를 중심으로 약 ±0.4m 정도의 오차를 보인다. 좌우동요의 경우 초기에는 1m를 중심으로 ±0.12m 이하의 오차를 보이다가 선수각 변경 후 2.4m를 중심으로 ±0.19m 이하의 오차를 보인다. 선수각은 계단 입력 직후에 7.3°를 지나 오버슈트 11.06°를 거쳐 제어 목표인 10°근방으로 수렴한다. PD 제어에 의한 제어력 역시 선수각 변환 제어 명령에 의해 제어력이 급격히 증가하였다가 시스템의 선수각이 제어 목표 근처로 수렴하면서 제어력이 감소하는 현상을 보인다.
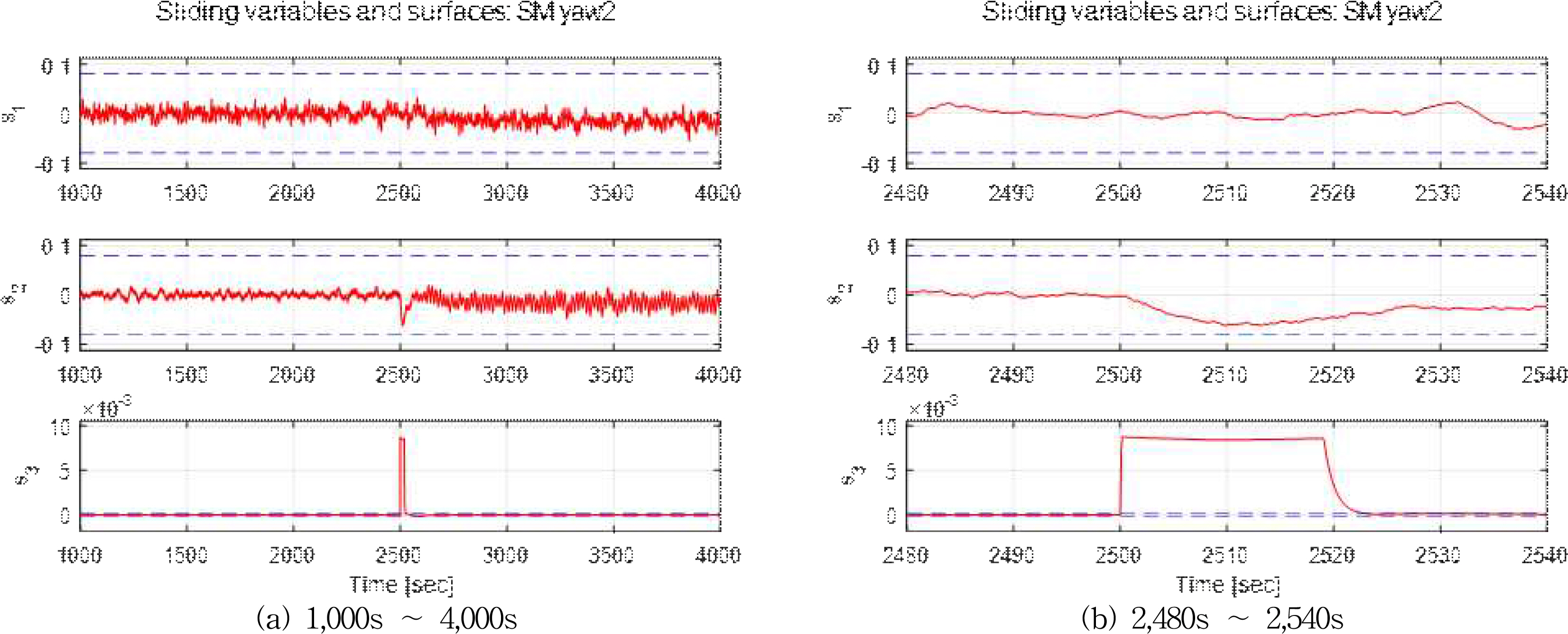
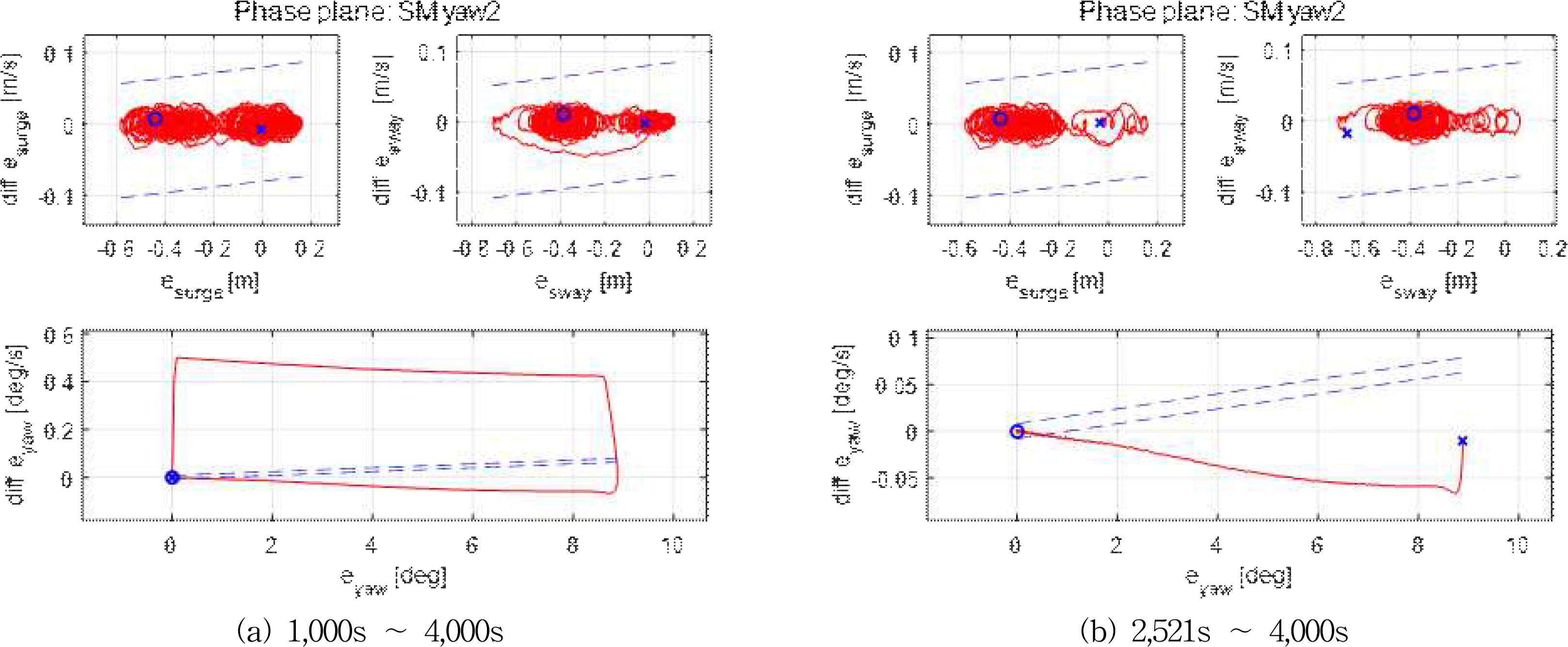
Fig. 10은 Case 2 시나리오에서 작동한 SM 제어기의 슬라이딩 평면 응답을 보인다. 여기서 s1, s2, s3는 각각 전후동요, 좌우동요, 선수동요 방향의 슬라이딩 변수를 나타내며, 점선은 슬라이딩 모드 제어기의 채터링 현상을 완화하기 위해 설정한 슬라이딩 평면 경계 변수 ϵ을 의미한다. 전후동요 및 좌우동요의 경우 슬라이딩 변수가 슬라이딩 평면 경계 내부에 위치하면서 s=0의 안정적인 슬라이딩 평면 응답을 보이고 있고, 선수동요의 경우 계단 입력이 시스템에 인가되었을 때 슬라이딩 변수가 슬라이딩 평면 경계 밖으로 이동했다가 일정한 시간 안에 슬라이딩 평면 경계 안으로 돌아오는 응답을 보인다. Fig. 10 (b)에서 보이는 바와 같이 선수각 제어에 대한 계단 입력이 인가된 순간 선수동요 방향의 슬라이딩 변수는 슬라이딩 평면의 경계를 벗어나고 약 23s 후 다시 슬라이딩 평면 경계 안으로 돌아오는 것을 알 수 있다. Fig. 11 (a)는 시뮬레이션 전 구간에서의 위상평면 응답이며, Fig. 11 (b)는 선수각 제어에 대한 계단 입력 이후의 오차 안정화를 확인하기 위한 짧은 구간의 위상평면 응답이다. 그림에서 ‘X’표시는 주어진 시뮬레이션 시간에서의 처음 오차 상태이며, ‘○’는 시뮬레이션에서 마지막 오차 상태이다. 결과로부터 오차와 그 미분값이 동시에 저감되면서 0으로 수렴하는 과정을 보이고 있다.
Case 2 시나리오에서의 SM 제어기와 PD 제어기의 결과 비교를 위해 구간별 오차와 소요 제어력을 Table 9와 Table 10에 정리하였다. 구간 1과 구간 2에서 전후동요 평균 오차는 SM 제어기의 경우 0.00m와 –0.38m가 PD 제어기의 경우 2.65m와 2.83m가 관찰되었다. 구간 2의 결과는 Case 1과 직접 비교가 가능한데 앞서 시나리오 소개에서 설명한 바와 같이 Case 2가 더 큰 환경 외력을 선박이 받는 조건이므로 전후동요의 경우에도 더 큰 환경 외력 작용에 따른 더 큰 밀림 현상이 관찰되고 있다. 소요 제어력의 경우에도 Case 1과 차이가 나타나고 있다. Case 1에서는 구간 2의 소요 제어력이 구간 1의 소요 제어력보다 작았으나, Case 2의 경우에는 전후동요 제어를 위해 소요한 제어력이 구간 1에과 구간 2에서 큰 차이가 없음을 확인할 수 있다. 좌우동요의 경우에도 구간 1과 구간 2의 평균 오차가 SM 제어기의 경우 0.00m와 –0.40m가 PD 제어기의 경우 –1.01m와 –2.43m이 관찰되었다. 또한 소요 제어력의 경우에도 SM 제어기는 구간 1과 구간 2에서 각각 7.71E+06kN과 1.22E+07kN이 관찰되었고, PD 제어기의 경우에는 7.96E+06kN과 1.29E+07kN이 관찰되었다. 선수각 변경 후 더 큰 환경 외력이 작용함에 따라 좌우동요 제어를 위한 소요 제어력과 오차가 커졌음이 확인되었다. 선수각 변경 과도구간을 포함하는 구간 3에서 좌우동요 제어를 위해 사용한 제어력은 SM 제어기가 2.55E+07kN, PD 제어기가 3.00E+07kN으로 SM 제어기가 PD 제어기 대비 약 15% 적은 제어력을 사용함을 알 수 있다. 선수동요의 경우 구간 3에서 최대 오차는 SM 제어기에서 발생하나, 선수각 제어를 위해 사용된 소요 제어력은 SM 제어기가 9.21E+08kNm, PD 제어기가 1.26E+09kNm로 SM 제어기가 PD 제어기 대비 약 26.9% 더 적은 제어력을 사용함을 확인하였다.
SM 제어기를 사용하여 Case 2의 시나리오로 시뮬레이션하였을 때 전후동요, 좌우동요의 구간 3에서의 차를 보면 ±0.58m(전후동요), ±0.71m(좌우동요) 이내로 SM 제어기에서 설정한 허용오차 emax 값 ±2m(전후동요), ±2m(좌우동요)를 만족함을 확인할 수 있다. 그러나 선수동요의 경우 앞선 Case 1과 마찬가지로 직접적인 계단 입력(0° → 10°)을 받았으므로 설정된 허용오차 emax ±1°를 만족하지는 못하였다. 이와 비교하여 PD 제어기의 구간 3에서의 오차를 살펴보면 전후동요 ±4.62m, 좌우동요 ±9.48m 이내의 오차가 발생하고 있다. 이를 근거로 다시 한번 제안된 SM 제어기가 터렛접속 작업에 더욱 적합한 DP 제어기라고 주장할 수 있다.
5. 결 론
본 논문에서는 최근 해양 작업의 종류와 실행 빈도가 증가함에 따라 다양한 선종과 해양 작업에 적용 가능한 강건한 DP 제어기법으로 고려되는 SM(Sliding mode) 제어 알고리즘을 소개하고, 그 유효성을 시뮬레이션을 통해 평가하였다. SM 제어기를 적용한 DP 시스템의 성능평가를 위한 시뮬레이터를 Matlab/SIMULINK 환경에서 구성하였다. 해당 시뮬레이터는 제어기 모듈, 선박 운동 모듈, 센서 모듈, 필터 모듈로 구성되었으며, 시뮬레이터에 적용된 선박 운동 모델, 센서 모델을 소개하였다. 선수부에 설치된 터렛의 접속 작업을 수행하는 FPSO를 가정하여 선수부 터렛 접속부의 위치를 동적으로 유지하는 SM 제어기를 설계하였다. SM 제어기의 안정성을 확보하기 위해 설계 단계에서 리아프노프(Lyapunov) 안정도 판별 이론을 적용하여 제어시스템의 안정성을 확보하였다. 제안한 DP 시스템을 위한 SM 제어기의 유효성 평가를 위해 PD 제어기를 구성하여 비교하였다. 환경 외력이 상대적으로 크게 작용하는 환경조건(Case 2)의 결과로부터 선수각 변경 과도상태를 포함하는 구간(구간 3)에서 SM 제어기를 사용할 때 PD 제어기를 사용하는 것보다 오차의 크기가 전후동요와 좌우동요에서 각각 ±4.62m → ±0.58m, ±9.48m → ±0.71m로 저감됨을 확인하였다. 따라서 선수부로 가정된 터렛접속부의 위치를 고정하고 작업해야 하는 터렛 접속 작업에서 SM 제어기를 사용하는 DP 시스템이 더 적합하리라 생각된다. 여기에 더하여 동일한 환경조건(Case 2)에서 선수각 변경 제어 전후의 모든 상태(구간 3)에서 사용된 제어력 절대값의 총합을 비교할 경우, 각각 3.05E+07kN → 3.01E+07kN(전후동요), 3.00E+07kN → 2.55E+07kN(좌우동요), 1.26E+09kNm → 9.21E+08kNm(선수동요)로 저감되었다. 이는 SM 제어기를 사용할 때 PD 제어기 사용할 때 보다 1.3%(전후동요), 15%(좌우동요), 26.9%(선수동요) 저감된 제어력을 사용함을 보이는 것이다. 이를 통해 SM 제어기는 PD 제어기에 대하여 작은 오차, 적은 제어력 사용의 상대적으로 우수한 제어 성능을 보이고 있음을 확인하였다. 이는 SM 제어기가 정상상태 오차 보정이 가능하고, 제어 대상 선박의 물리적 특성을 고려한 제어 파라미터 조정이 가능하며, 전후동요, 좌우동요, 선수동요의 각 운동 간 간섭을 고려하여 제어를 수행하는 MIMO(Multi input multi output) 시스템이기 때문에 갖는 장점으로 판단된다. 특히, 제어 대상 선박의 응답 특성을 직관적으로 고려하는 제어 파라미터 선정을 통한 제어 성능 조정은 점점 더 다양해지고 복잡해지는 해양 작업 수행에서 큰 매력으로 작용할 것으로 기대된다.
제안된 SM 제어기의 신뢰성 확보를 위해 향후 실험을 통한 성능평가 연구를 희망하며, 성능 향상을 위해 변화하는 해양환경에서 선박 또는 해양구조물에 작용하는 환경 외력을 정밀하게 추정하는 기술개발을 추진하고자 한다.
Acknowledgements
본 논문은 해양수산부의 국가연구개발사업인 “전기추진 차도선 및 이동식 전원공급시스템 개발” 과제(20200469-01, PMS4980)와 선박해양플랜트연구소 주요사업인 “친환경 선박 연료 신뢰성· 안전성 평가기술 개발” 과제(PES4301)의 지원으로 수행되었음을 밝히며, 연구비 지원에 감사드립니다.