Optimal Route Planning for Maritime Autonomous Surface Ships Using a Nonlinear Model Predictive Control

Article information

Abstract

1. Introduction

A ship's route should be determined before the start of a voyage with consideration given to a ship's maneuvering behavior as well as the critical factors on the route features. With the increase of interest in developing Maritime Autonomous Surface Ships (MASS), an optimal route planning is gradually gaining popularity as one of the important subsystems for the autonomy of modern marine vessels (Li et al, 2019). It should be mentioned that planning an optimal route is of great importance in order to achieve fully autonomous navigation at sea, which can contribute to ensuring safe and efficient autonomous navigation operations of ships.

For route planning optimization, it is imperative to ensure the safety of ship operations at sea when a ship follows a predefined route. The route planning that does not take into account the maneuvering performance of a ship can cause large deviations from the predefined route, resulting in navigational casualties such as grounding and collision. In other words, the route planning algorithm for MASS should take into account the accurate maneuvering performance of a ship, i.e., the complicated interactions between the hull, propeller, and rudder during its operation when generating a reference route. However, numerous past studies in the field of route planning for marine vehicles have been devoted to employing a simplified mathematical ship model in the assumption that vehicles use a constant velocity during their operations for simplicity. For example, Rhoads et al. (2010) dealt with the problem of steering a fixed-speed autonomous underwater vehicle to the desired target position in minimum time by solving a dynamic Hamilton Jacobi Bellman equation for the optimal “time-to-go” and related optimal feedback control law. The velocities of autonomous marine vehicles were maintained constant in Zeng et al. (2017), where a distributed shell-space decomposition for rendezvous route planning by means of a B-spline-based quantum particle swarm optimization technique. Due to changes in engine power and rudder deflection, it has been observed in real operations that marine vehicles experience continual variations in their velocities such as surge, sway and yaw velocities. Given this, this paper was motivated to take into account the nonlinear dynamic aspect of a maneuvering ship when performing route planning optimization by means of a nonlinear Model Predictive Control (MPC) technique.

MPC has its roots in optimal control, and its fundamental principle is to use a nonlinear dynamic model to forecast system behavior and optimize the forecast with the aim to make the best decision (Rawlings et al, 2017). When solving a route planning problem, MPC has the advantage of efficiently handling hard constraints for the input constraints and soft constraints for the output or state constraints. Sandeepkumar et al.(2022) claimed in their paper that “MPC owes its popularity to its constraint handling capabilities enabling maximum performance to be extracted when the system is pushed to the operational limits”.

The present study is devoted to the route planning optimization problem for marine vehicles, using a nonlinear MPC model combined with a Maneuvering Modelling Group (MMG) model. The complicated mutual interactions between the hull, propeller, and rudder during manoeuvres can be taken into account by adopting the MMG model for route optimization, consequently capable of accurately dealing with complex constraints.

2. Problem formulation

This section will present the problem of distance-optimal route planning of marine vehicles, with a detailed description of the mathematical ship model and MPC approach in the included sub-sections.

2.1 Route planning

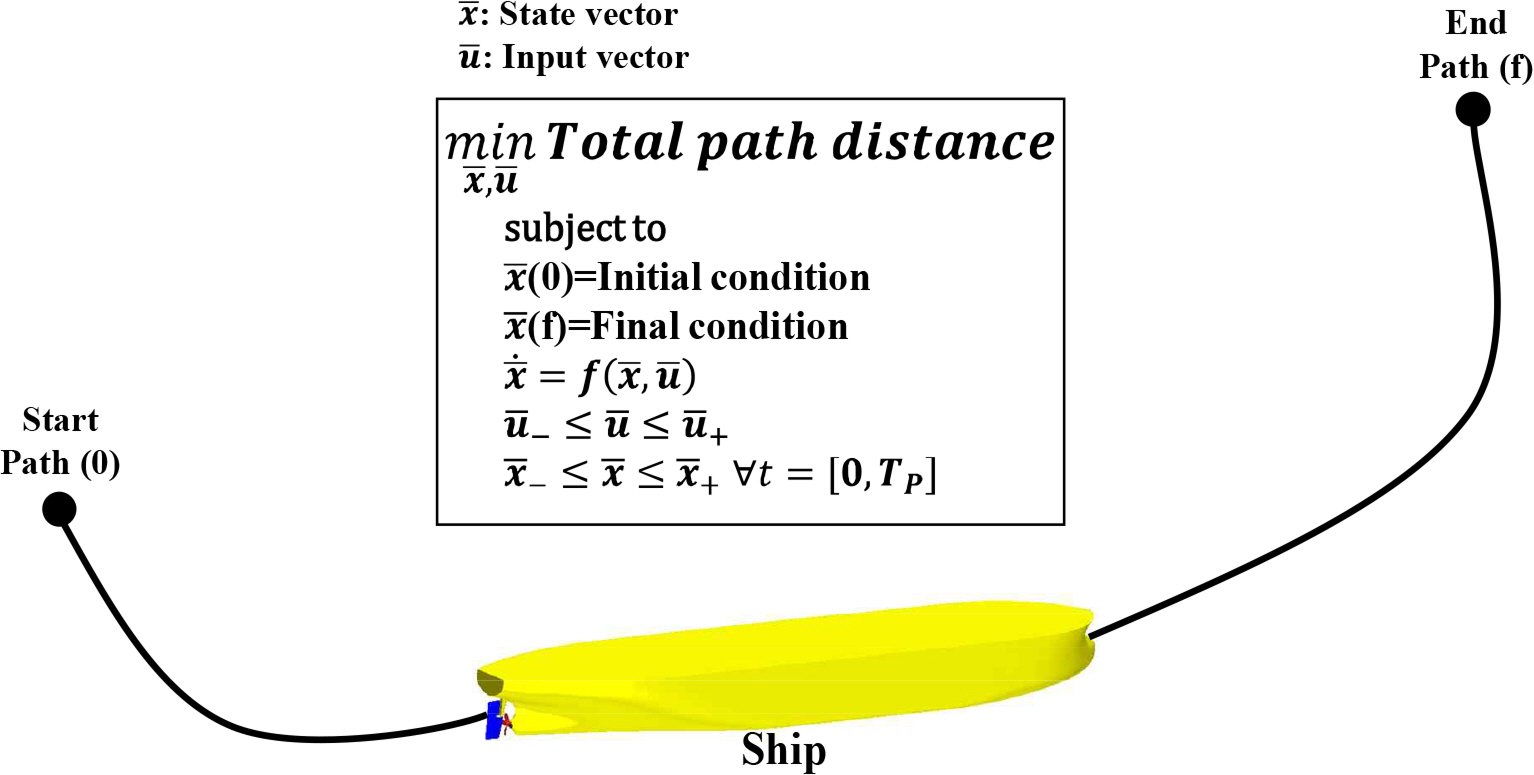
Marine vehicles should be capable of following the predefined route based on the Estimated Time of Arrival (ETA), ensuring navigational safety at sea. Thus, a route planning procedure should impose constraints on states (e.g., kinematic parameters) or outputs (e.g., engine power or rudder angle) for safety and operational reasons, as depicted in Fig. 1.

Fig. 1.

Sketch of distance-optimal route planning for marine vehicles by means of an MPC approach

2.2 Ship geometry and coordinate systems

In this study, the well-known benchmarking KVLCC2 (KRISO Very Large Crude Carrier 2) was adopted for the optimal ship route planning problem. Fig. 2 depicts the overview of the ship geometry, which is characterized by a traditional single rudder / single propeller configuration, and the principal particulars of the ship are listed in Table 1.

Fig. 2.

KVLCC2 geometry with a semi-balanced rudder and a propeller

Table 1.

Main particulars of the KVLCC2

For the route planning problem for the ship, three right-handed coordinate frames were defined as displayed in Fig. 3: (1) Earth-fixed frame (o_e − x_ey_ez_e), (2) Ship-fixed frame (o_s − x_sy_sz_s), and (3) Rudder-fixed frame (o_r − x_ry_rz_r).

Fig. 3.

The coordinate systems of the ship adopted in this study

2.3 Nonlinear state space model

The governing equations of rigid body motion (for 3 DoF) were used to resolve the nonlinear dynamics of the ship operating at sea, which can be expressed as follows (Yasukawa, H., & Yoshimura, Y.,2015):

(1) (m+mx)u˙-(m+my)vr-xGmr2=X(m+my)v˙+(m+mx)ur+xGmr˙=Y(IZG+x2Gm+JZ)r˙+xGm(v˙+ur)=N

in which m is the mass of body (unit: kg)

u, v, r are the surge/sway/yaw velocities (units: m/s, m/s, and deg/s, respectively)

u̇, v̇, ṙ are the surge/sway/yaw accelerations (units: m/s², m/s², and deg/s², respectively)

m_x, m_y are the added masses of x axis direction and y axis direction (unit: kg)

x_G is the longitudinal coordinate of center of gravity of the ship (unit: m)

I_ZG is the moment of inertia about the z axis (unit: kg·m²)

J_Z is the added moment of inertia about the z axis (unit: kg·m²)

X, Y are the surge/sway resultant forces acting on the ship (unit: N)

N is the yaw resultant moment acting on the ship (unit: N·m)

The hydrodynamic forces (X, Y) and moment (N) in Eq. (1) are decomposed into three components in the MMG model: the bare hull, rudder, and propeller.

(2) X=XH+XR+XP+XWY=YH+YR+YWN=NH+NR+NW

where the subscripts H, R, P denote hull, rudder, and propeller, respectively. X_W,Y_W, N_W mean the external forces and moment acting on the hull induced by waves. In this work, the nonlinear and linear MMG models were used for the validation study about the accuracy of the ship’s maneuvering performance. The hydrodynamic derivatives for the nonlinear maneuvering MMG model are expressed in Eq. (3), whereas the hydrodynamic derivatives for the linear MMG model are given in Eq. (4).

(3) XH=Xuu+Xvvv2+Xvrvr+Xrrr2+Xvvvvv4YH=Yvv+Yrr+Yvvvv3+Yvvrv2r+Yvrrvr2+Yrrrr3NH=Nvv+Nrr+Nvvvv3+Nvvrv2r+Nvrrvr2+Nrrrr3

(4) XH=XuuYH=Yvv+YrrNH=Nvv+Nrr

in which X_u, X_vv, X_vr, X_rr, X_vvvv, Y_v, Y_r, Y_vvv, Y_vvr, Y_vrr, Y_rrr, N_v, N_r, N_vvv, N_vvr, N_vrr, and N_rrr are called the hydrodynamic derivatives. For more details on the MMG model, reference can be made to Yasukawa, H., & Yoshimura, Y. (2015).

It has to be stated that the hydrodynamic coefficients, propeller thrust, rudder forces and moments for the KVLCC2 were determined from the captive model experiment reported in Yasukawa, H., & Yoshimura, Y. (2015). In addition, second-order wave loads for the KVLCC2 were determined from the circular motion tests reported in Jeon et al. (2021).

The numerical simulations of the turning, zigzag characteristics were carried out to ensure that the nonlinear MMG model accurately assessed the maneuvering behavior of the KVLCC2 (Fig. 4, 5, and 6). It was found that the linear MMG model could not estimate the maneuvering behaviors accurately due to the only consideration of the linear terms on the right-hand side of Eq. (3), as shown in the figures. Such considerations lowered the accuracy of the hydrodynamic forces and moment acting on the ship, demonstrating that the linear MMG model cannot accurately predict the complicated interaction between the hull, propeller, and rudder during maneuvers.

Fig. 4.

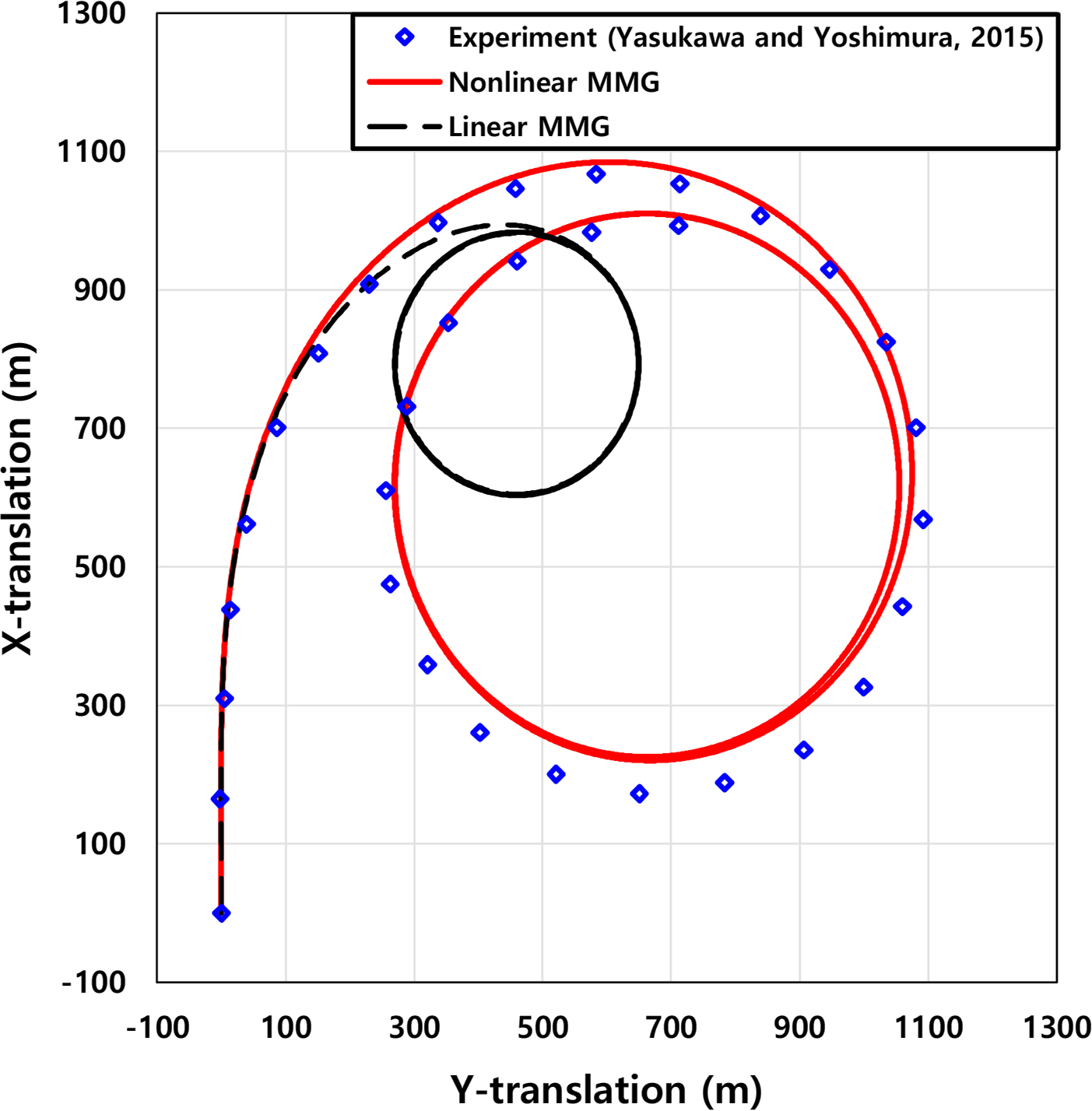
Comparison of the trajectory between the experiment and MMG models for the turning maneuver in calm water (rudder angle=35°)

Fig. 5.

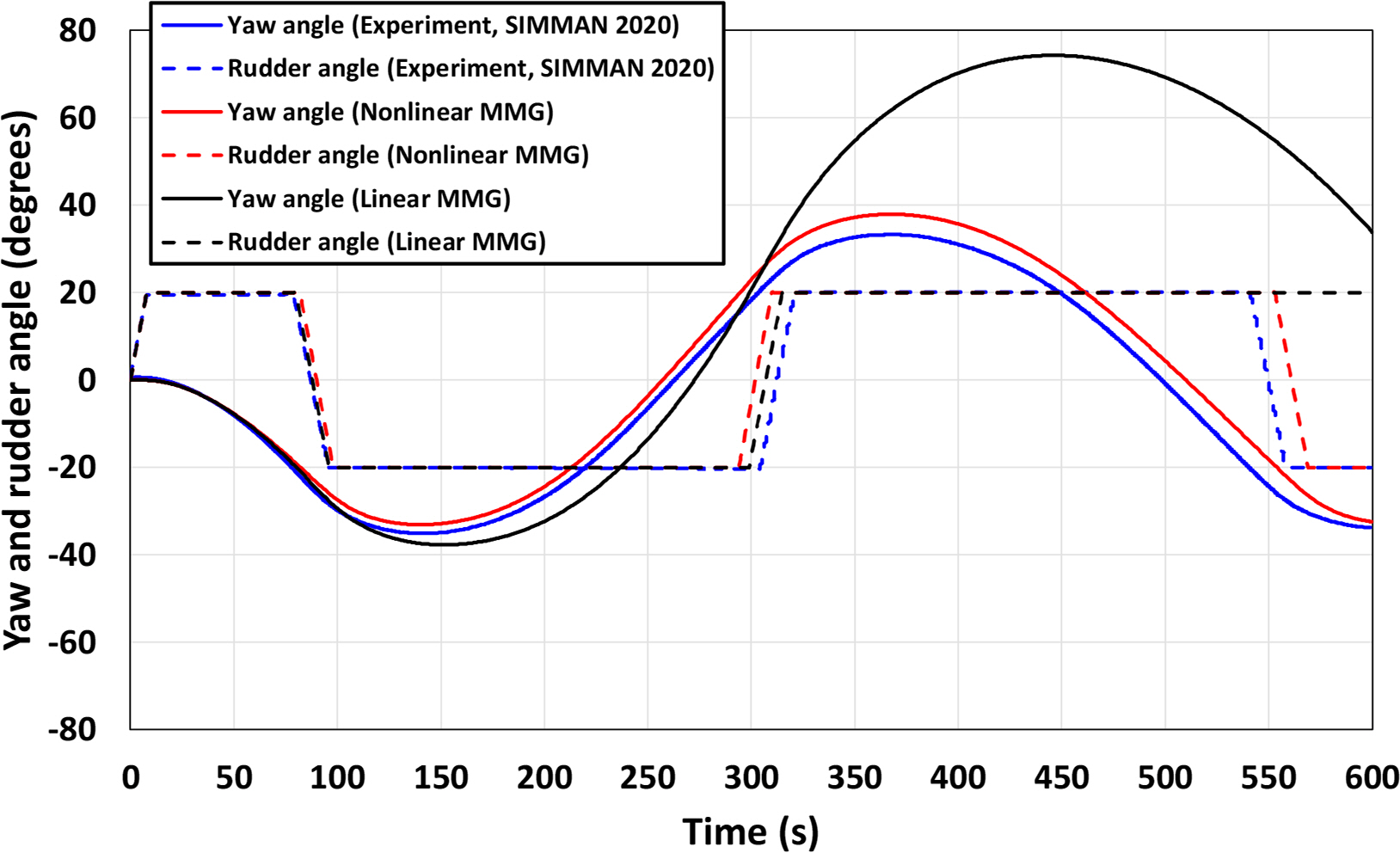
The time histories of the yaw angle and rudder deflection during the 20°/20° zigzag maneuver in calm water

Fig. 6.

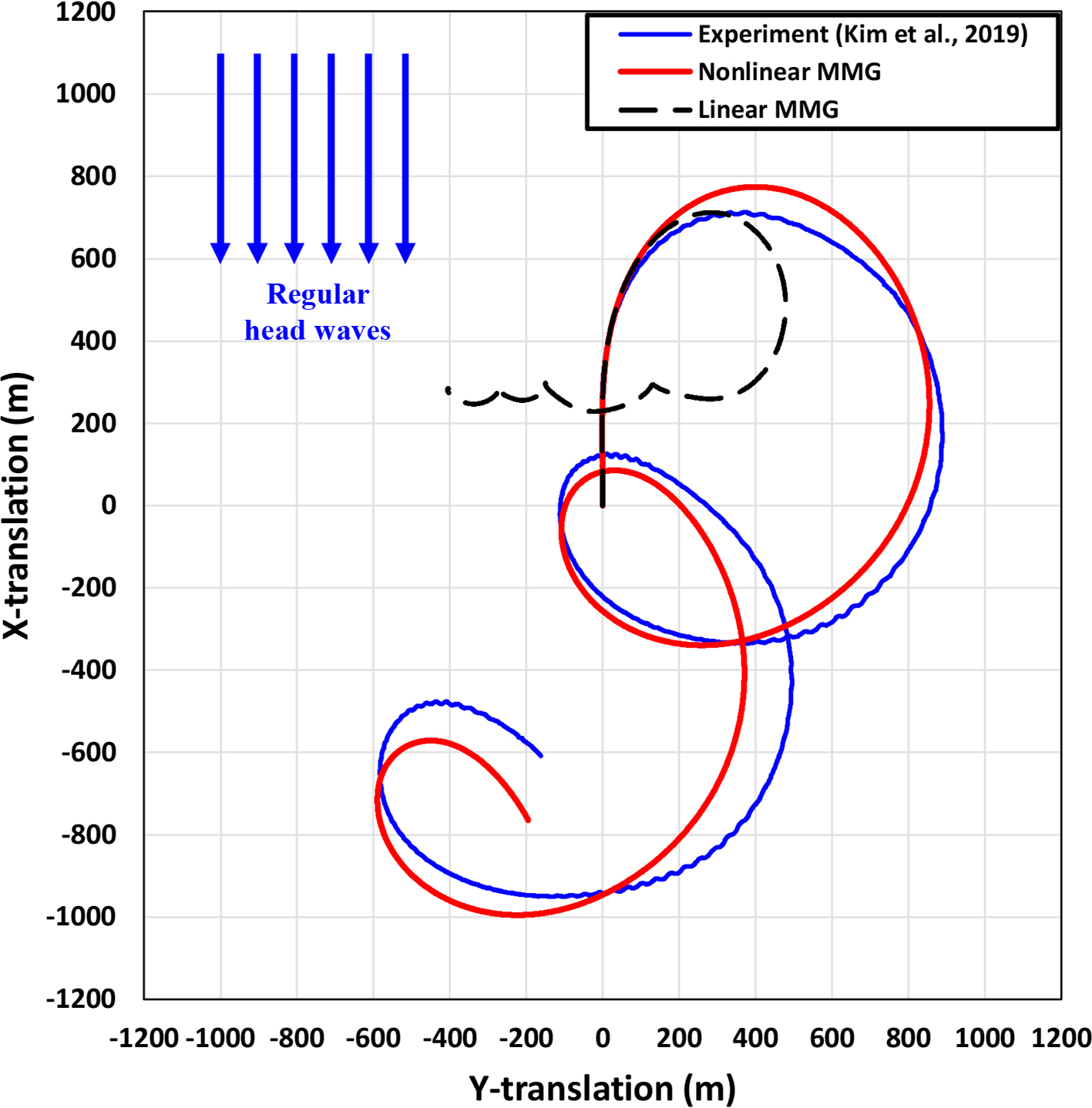
Comparison of the trajectory between the experiment and MMG models for the turning maneuver in regular head waves (rudder angle=35°, wave height=6.4m, wave length=224m)

When using the nonlinear MMG model adopted in this work, the agreement is reasonable for the predicted ship trajectories and kinematic parameters during the maneuver.

Based on the aforementioned equations, the nonlinear dynamic system of the ship for the MPC can be given in state-space form as a set of continuous Ordinary Differential Equations (ODEs) consisting of the state (x̄) and manipulated inputs (ū) vector as follows (Sandeepkumar et al, 2022):

(5) x¯˙=[u˙v˙r˙x˙y˙ψ˙]=f(x¯,u¯)=[A-1b1b2]A=[(m+mx)000(m+my)xGm0xGm(IZG+x2Gm+JZ)]b1=[X(m+my)vr+xGmr2Y-(m+mx)urN-xGμr]b2=[ucosψ-vsinψusinψ+vcosψr]

in which x̄ = [u v r x y ψ]^T is the state vector, ū = [n δ ]^T is the manipulated input vector. x and y are the x and y position expressed with respect to the earth-fixed coordinate (unit: m), ψ is the ship's heading angle (unit: degree), n is the propeller rotational speed (unit: RPS), δ is the rudder angle (unit: degree).

3. Results (Case study)

This section was organized to solve the route planning optimization problem for the KVLCC2 in accordance with the modelling setup described in Section 2, taking into account the MPC controller parameters (Table 2) and the imposed constraints (Table 3).

Table 2.

MPC controller parameters applied in this work

Table 3.

Imposed constraints on the state and manipulated variables

An iteration process for finding an optimum is required in the optimization toolbox solver. The solver begins at a given initial value x₀ and then performs intermediate computations that result in a new point x₁. It then repeats the process in order to obtain successive approximations x₂, x₃, ⋯ of the local minimum. It should be highlighted that the number of iterations in the optimization computation depends on the solver's stopping criteria consisting of Step tolerance and Function tolerance. Step tolerance is a lower bound on the size of a step, indicating the norm of (x_i − x_{i + 1}), whereas Function tolerance is a lower bound on the change in the objective value during a step (|f(x_i) − f(x_{i + 1})|). For the route planning optimization in this work, the iterations end if |x_i − x_{i + 1}| < Step tolerance and |f(x_i) − f(x_{i + 1})| < Function tolerance.

The imposed constraints on the state and manipulated input variables were determined to simply demonstrate the performance of the nonlinear MPC model proposed in this work for the optimal route planning problems. As reported in Table 3, the propeller rotational speed was constrained from −1RPS to 1.78RPS, and the rudder deflection was bounded from −35° to 35° based on the ship particulars. It should be noted that the surge velocity for the KVLCC2 was constrained between 0 and 3.5 m/s (6.8 knots) based on the assumption that the ship was operating in an area with a speed restriction of 3.5 m/s. The constraints of the parameters related to the ship velocities, propeller, and rudder characteristics shown in Table 3 were imposed in a realistic way based on the experimental results of the KVLCC2 (Kim et al, 2019). The results obtained for solving a class of nonlinear constrained route planning optimization problems using the nonlinear MPC approach are presented in Fig. 7 and Fig. 8. Five different cases for distance-optimal ship route planning problems were taken into consideration within this work; positions (−10LBP, −10LBP) and (0,0) in Fig. 7 indicate the initial and final positions of the ship, respectively. It should be noted that Case 4 was carried out in the regular head wave condition, while Case 5 was performed in the regular head sea together with the ahead current condition (0.5 knots). The effects of the current on the ship's performance can be solved within the hydrodynamic damping terms, considering the direction and speed of the current to be applied.

Fig. 7.

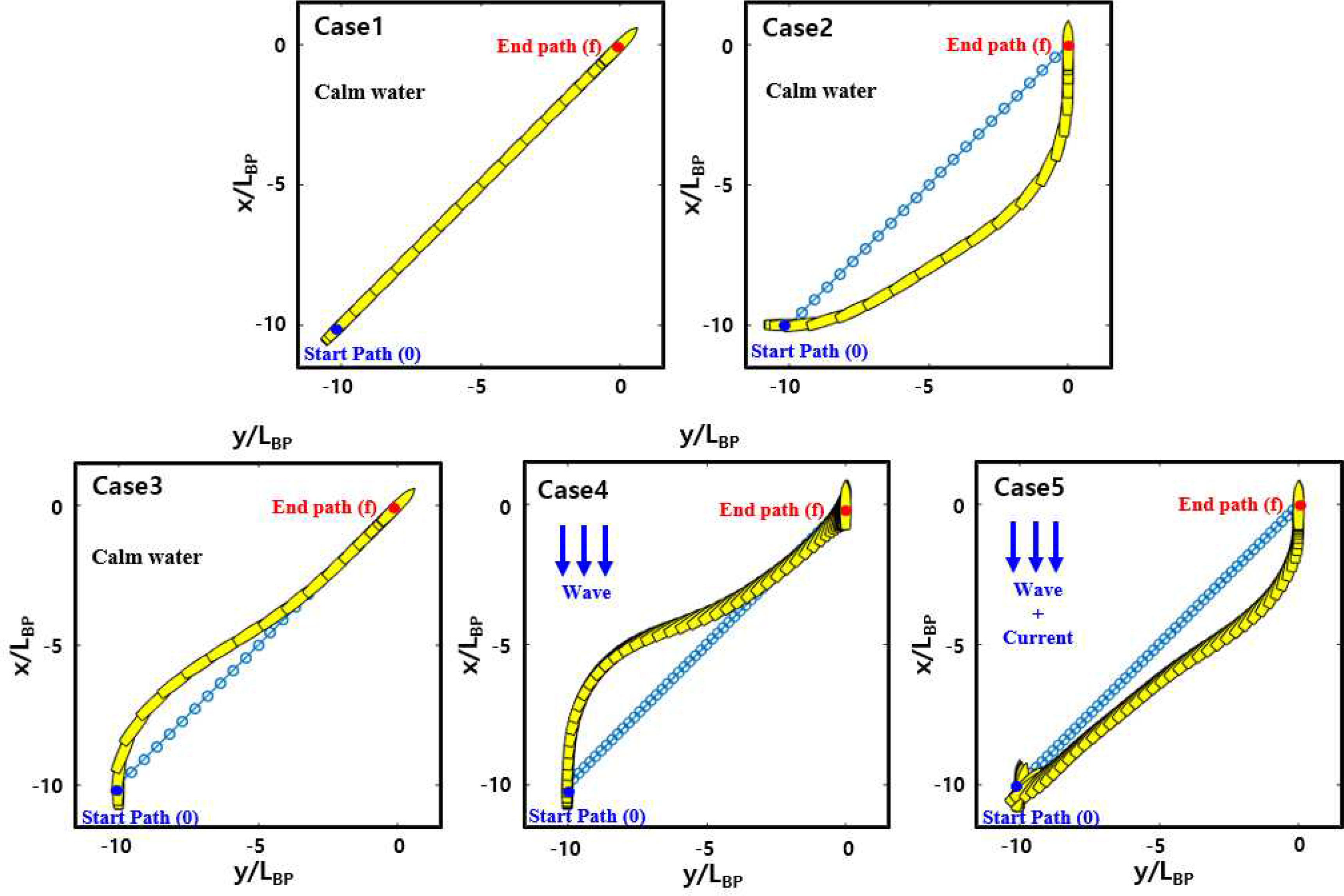
The ship trajectories generated by the nonlinear MPC controller (Cases 1–3: calm water; Case 4: regular head waves; Case 5: regular head waves together with the ahead current).

Fig. 8.

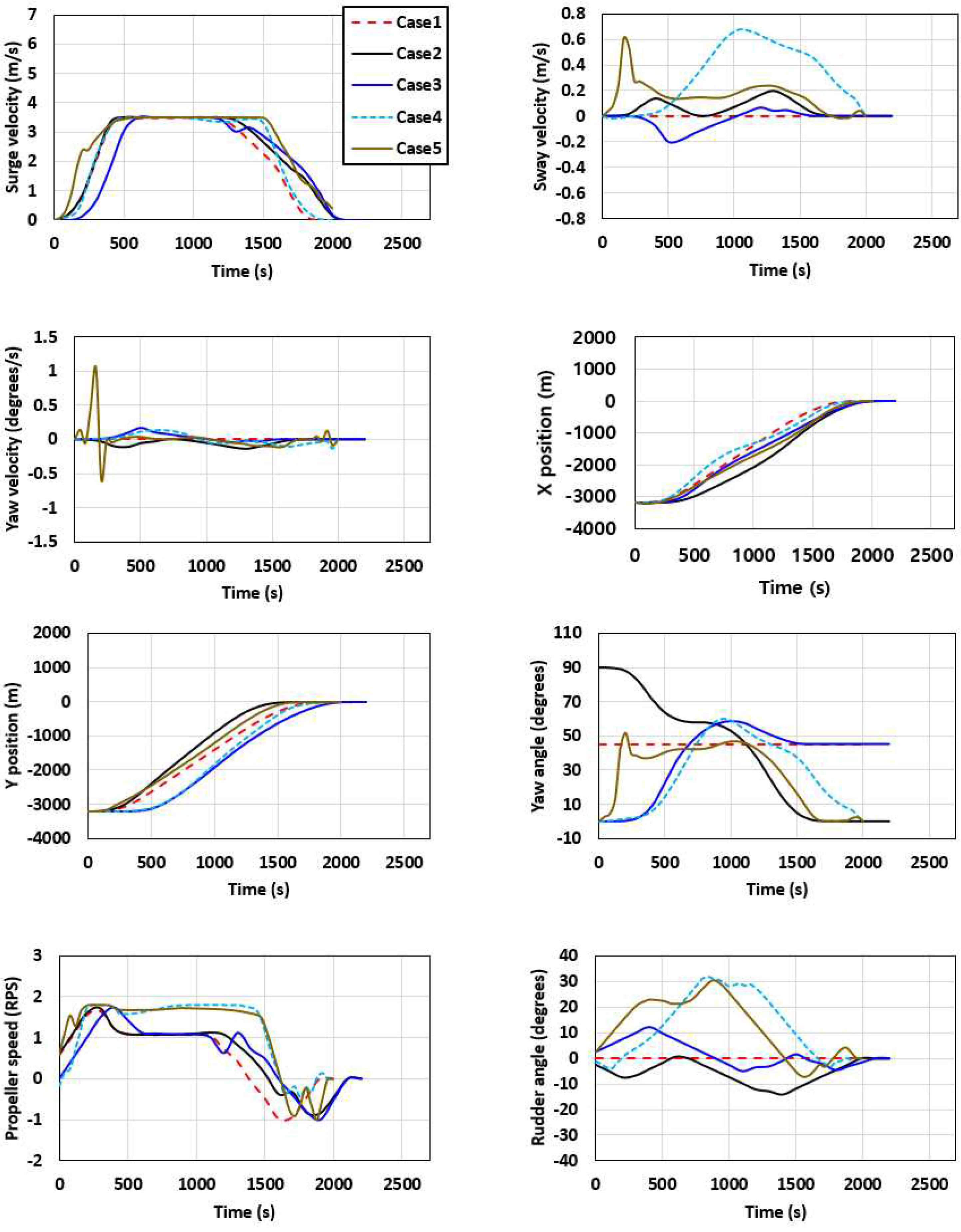
The state (x̄) and manipulated (ū) variables estimated by the nonlinear MPC approach (Cases 1–3: calm water; Case 4: regular head waves; Case 5: regular head waves together with the ahead current).

The ship should comply with all the imposed constraints reported in Table 3 while operating from its initial position to its final position in all cases. As clearly evidenced in the figures, the optimization problems were observed to be successfully solved by the MPC, satisfying the equality and inequality constraints. In other words, the ship route was generated with the consideration of the nonlinear dynamics of the system and all the constraints regarding the state (x̄) and manipulated (ū) variables.

4. Conclusions and discussion

In the present work, an optimal ship route planning model for autonomous marine navigation has been proposed by means of the nonlinear MPC approach together with the nonlinear MMG model.

Given the previous studies related to optimal ship route planning, the effectiveness of the applied controller is generally evaluated depending on whether the imposed constraints on the state (x̄) and manipulated (ū) variables satisfy equality and inequality conditions. In this regard, it can be argued that the effectiveness of the MPC controller adopted in this study is demonstrated by presenting that the optimal ship route was successfully generated with the satisfaction of the nonlinear dynamics of the ship and all the constraints for the state and manipulated variables.

It has to be stated that the comparison between the MPC controller and the PID controller in terms of optimal route planning is not feasible since the PID controller does not take into account the cost function. When considering another controller that can consider the cost function for comparison, it is thought that the optimal ship route varies depending on the applied cost function. Given this, the comparison between the MPC controller reported in this study and other controllers for optimal ship route planning was not a focus of this study.

Given that the ship route generation system capable of accounting for the nonlinear dynamics of the ship and equality/inequality constraints is essential for safe autonomous navigation, it is expected that this paper will contribute to the field of autonomous vehicles by demonstrating the performance of the proposed optimal ship route planning model. Proposed future work should incorporate the presence of different environmental loads, as these will have a noticeable effect on the ship route planning optimization problem for marine vehicles.

Article information Continued