Implementation of Ship Trajectory Following Algorithm
Article information
Abstract
As interest in autonomous ships continues to grow, researchers around the world are dedicating themselves to the development of relevant technologies. However, these technologies are not yet perfect. Several technical problems remain unresolved. To address these problems, this study presents the implementation of a ship trajectory algorithm for group navigation, where followers can navigate by following the trajectory of a leader. The algorithm works by storing the leader's trajectory as a follow-point and by calculating the azimuth using the line-of-sight guidance law to reach it. A course-keeping controller based on PD control is implemented to follow the target course and a speed control algorithm is designed to prevent collisions. Sea experiments were conducted using 1 m class small RC model boats to verify the proposed algorithm. The follower successfully navigated by following the leader's trajectory and maintained the designated distance to the forward boat. This study is significant in that it implements an algorithm for the follower to follow the trajectory of the leader rather than directly following it as in conventional methods, and verifies it through sea experiments.
1. Introduction
Recently, autonomous ships are an important issue for the maritime industry. Shipping-advanced countries such as the European Union, Norway, the UK, Finland and Japan are leading the technology development in an effort to dominate the autonomous ship market (Park et al., 2018; Kim, 2022). However, in order to commercialize autonomous ships, several technical problems needed to be solved. In other words, technologies such as ship-to-shore communication, cybersecurity, equipment failure prediction and maintenance must be perfectly developed(Jung et al., 2019; Chae et al., 2020). These problems become even more fatal when they occur during ocean voyages.
The authors proposed a group navigation system as a method to address the problems facing autonomous ships (Choi and Jun, 2022). In this system, a leader and several followers are grouped together to navigate. The leader navigates along the designated route from the starting point to the destination, and the followers follow the leader’s route autonomously. In a previous study, a group navigation system consisting of one leader and two followers was established, and simulations were performed using a scale model of an actual ship.
The aim of this study is to implement a ship trajectory tracking algorithm, and to verify through sea experiments using 1 m class RC (Radio Control) model boats. The algorithm is designed for the follower to receive the leader’s position in real-time, store it as a follow-point, calculate the azimuth to the follow-point, and follow it. As the follower navigates along the leader’s trajectory, it can safely navigate without deviating from the predetermined route.
The structure of the paper is as follows. In Chapter 2, the ship trajectory following algorithm, course-keeping and speed control of the ship are described, along with the ship dynamic model required for controller design. In Chapter 3, the ship dynamic model is identified through turning experiments using 1 m class RC model boats, and the parameters of course-keeping controller are tuned. Then, experiments are conducted to verify the implemented ship trajectory following algorithm. Finally, Chapter 4 presents conclusions and future research objectives.
2. Trajectory following algorithm
2.1 Trajectory following method
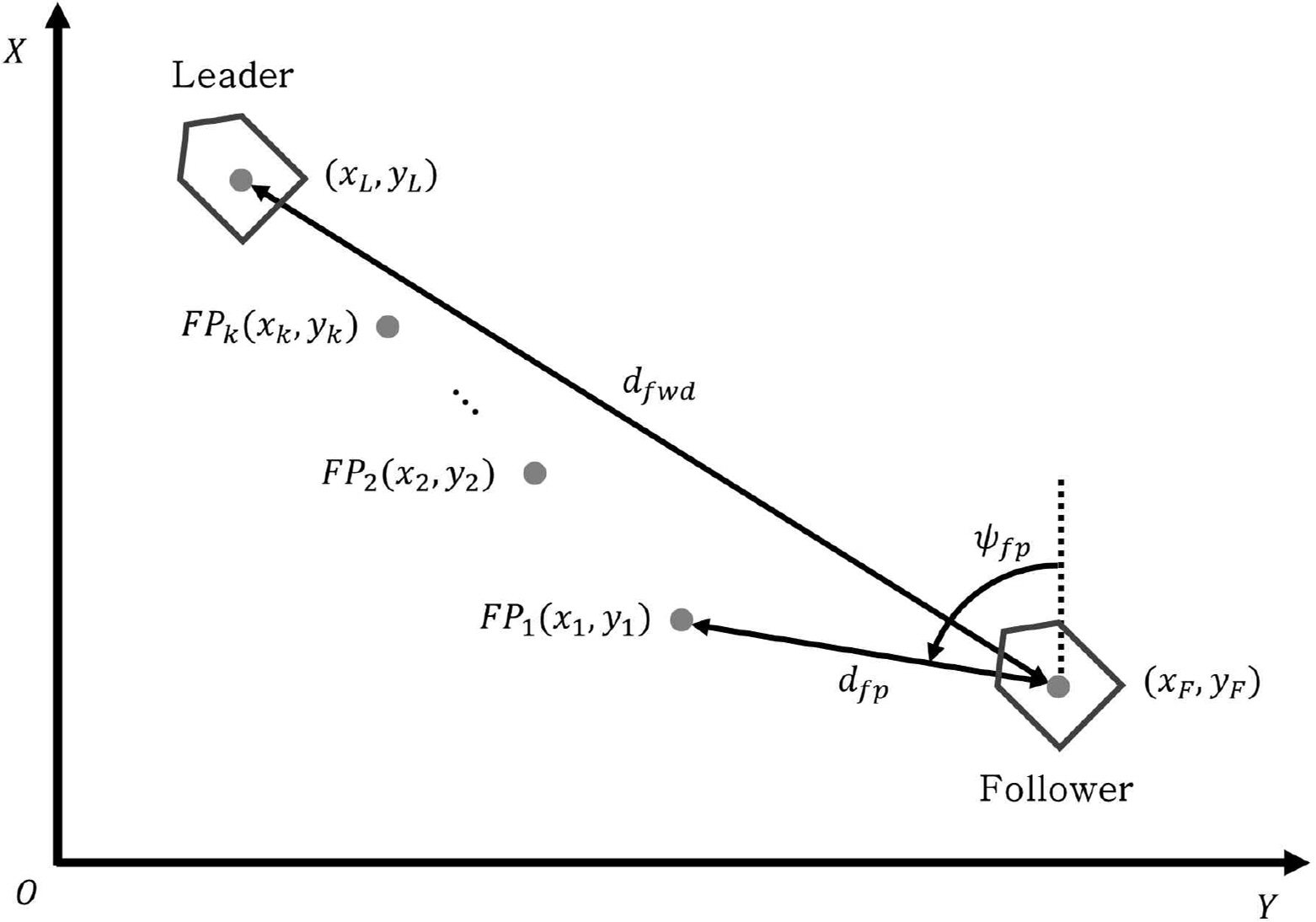
Ship trajectory following is a method where a follower navigates along the trajectory of a leader. This approach ensures that the follower can safely navigate without deviating from the leader’s planned route. Moreover, since it requires only minimal speed control to prevent collisions between ships, this method is relatively simple to implement. Fig. 1 shows the structure of the ship trajectory following.
Here, (xF, yF) is the current position of the follower, (xL, yL) is the current position of the leader, (xk, yk) is the k-th follow-point (FPk). And dfp is the distance from follower to the first follow-point, ψfp is the azimuth from follower to the first follow-point and dfwd is the distance from follower to the forward ship, which are calculated using the line-of-sight guidance law as shown in Equations (1) to (3).
When the leader starts navigating from the starting point to the destination, the follower receives the leader’s position every second and stores it as a follow-point. Also, the follower calculates the azimuth (ψfp) and distance (dfp) from its current position (xF, yF) to the first follow-point (x1, y1) every second. If the dfp is less than a pre-set convergence radius, the next follow-point is automatically updated to the first follow-point. Then, the follower calculates the ψfp and dfp to the updated first follow-point and continues to follow it. The convergence radius is set to 7.5 m, considering the GPS position accuracy and the steering characteristics of the experimental boats.
The follower calculates the distance to the forward ship (dfwd) every second and controls its speed based on the forward safe distance (FSD), which is the distance between ships set to prevent collisions. The FSD was set at 12.2 times the length of the ship by introducing the concept of ship safety domain(Choi and Jun, 2022).
2.2 Controller design
(1) Course-keeping control
To follow the desired course, the researchers designed a course-keeping controller based on PD (Proportional-Derivative) control. The experimental boats used in this study are small model boats made of fiberglass with a length of about 1 m and are vulnerable to external forces such as wind and current, causing significant leeway. For this reason, COG (Course Over Ground) was used as the control variable instead of the ship’s yaw angle. Fig. 2 shows the block diagram of the course-keeping controller used in this study.
Here, KP is the proportional gain, KD is the derivative gain, ψd is the ship’s desired course, ψ is ship’s current course, e is course error, δc is the command rudder angle and δ is the ship’s actual rudder angle.
The COG (ψ) is obtained from the GPS sensor and is fed back to the controller. The command rudder angle (δc) is calculated using ψ and is input to the servo motor to control the rudder angle. The PD control formula for calculating the command rudder angle is shown in Equation (4).
To ensure proper operation of the designed course-keeping controller, the PD control parameters KP and KD must be tuned to obtain optimal values. In this study, tuning of the parameters was carried out using the Nomoto model as the ship dynamic model.
The Nomoto model represents the motion of a ship with the rudder angle (δ), rate of turn (r) and steering quality indices (K, T1, T2, T3), as shown in Equation (5) (Nomoto et al., 1957). This model has the advantage of providing an easy way to understand the dynamics of a ship, although it has many limitations in expressing the highly nonlinear motion of a ship.
Assuming that T = T1 +T2 −T3, Equation (5) can be expressed as a first-order equation.
If Equation (6) is expressed as a transfer function that represents the relationship between the input and output, it can be represented as Equation (7).
Since the ship dynamic model is represented by the rudder (input) and rate of turn (output), it is necessary to estimate the unknown model parameters based on rudder angle and rate of turn data obtained from the system. To estimate the parameters, an ARX (AutoRegressive with eXternal input) model was used.
The ARX model is widely used for system identification in submarines, small sailboats, small model boats, and similar systems (Velasco et al., 2007, Kim, 2011, Dantas et al., 2013, Tranzatto, 2015, Choi and Jun, 2020). The ARX model can be expressed as Equations (8) to (10) (Ljung, 1987).
Where, q is a delay operator, u(t) is the input at time t, y(t) is the output at time t, e(t) is the disturbance signals or noise. A(q) is a polynomial of output, B(q) is a polynomial of input, na is number of poles, nb is number of zeros, nk is pure time-delay in the system. The parameters a and b are estimated by the least squares method.
(2) Speed control
To avoid ship collisions, an algorithm was developed to control the speed of the follower. The algorithm calculates the distance to the forward ship (dfwd) every second and compares it to the pre-set FSD. Based on the results of the comparison, an appropriate pulse width signal is sent to the ESC (Electronic Speed Controller) to adjust the propeller rotation. The speed control algorithm for the follower is described as follows.
If dfwd is between FSD and 1.2 times FSD (FSD≤ dfwd ≤ 1.2 × FSD), the pulse width is set to 1,570 μs to maintain the distance to the forward ship. If dfwd is greater than or equal to 0.5 times FSD and less than FSD (0.5 × FSD≤ dfwd < FSD), the pulse width is decreased to 1,560 μs to increase the distance to the forward ship. If dfwd is greater than 1.2 times FSD (1.2 × FSD < dfwd), the pulse width is increased to 1,580 μs to prevent excessive increase in the distance between ships. If dfwd is less than 0.5 times FSD (dfwd < 0.5 × FSD), the pulse width is set to 1,500 μs to stop the propeller rotation.
3. Experiments and results
3.1 Experimental boat
The three boats used in the experiments are 1 m class model RC boats, Leader, Follower 1, Follower 2, as shown in Fig. 3. The specifications of the experimental boats are listed in Table 1. The length of the experimental boats is about 1.3 m and 0.9 m, with a maximum draft of around 10 cm and 7 cm. Therefore, the boats are highly influenced by sea conditions such as wind or waves.
The Leader and Followers have the same hardware configuration, but differ in their specifications. Each boat is equipped with a propeller, BLDC (Brushless Direct Current) motor, ESC, rudder and servo motor. Pulse width modulation controls the BLDC motor and servo motor with a pulse frequency of 50 Hz (20 ms). The BLDC motor stops at a pulse width of 1,500∼1,550 μs, and rotates clockwise when the pulse width exceeds 1,550 μs, with the rotation speed increasing up to a maximum pulse width of 2,000 μs. The servo motor is at 0° (midship) when the pulse width is 1,500 μs, and rotates 1° to starboard for every 10 μs increase in pulse width, and 1° to port for every 10 μs decrease. Two LiPo (Lithium-Polymer) batteries power the boats, and the ESC supplies electricity to the BLDC motor and servo motor.
To measure the heading angle, an IMU (Inertial Measurement Unit) is installed on each boat with 0.5° accuracy. A GPS sensor is also installed with 2.5 m position accuracy, 0.05 m/s velocity accuracy, 0.3° course accuracy.
The control board is a LattePanda, which is an SBC (Single Board Computer) based on the Windows 10. It includes a single board microcontroller, Arduino Leonardo, to collect data from the IMU, GPS and control the BLDC motor and servo motor. It is powered by a LiPo battery and operates the IMU and GPS sensors.
To facilitate communication between the boats, a Wi-Fi mobile router and an RF receiver are installed on each boat. TCP/IP socket programming is used for Wi-Fi communication, and the three boats exchange information including position, speed, course, and heading. RF communication is used as a backup method to retrieve the boat in case of system failure.
3.2 Identification experiment
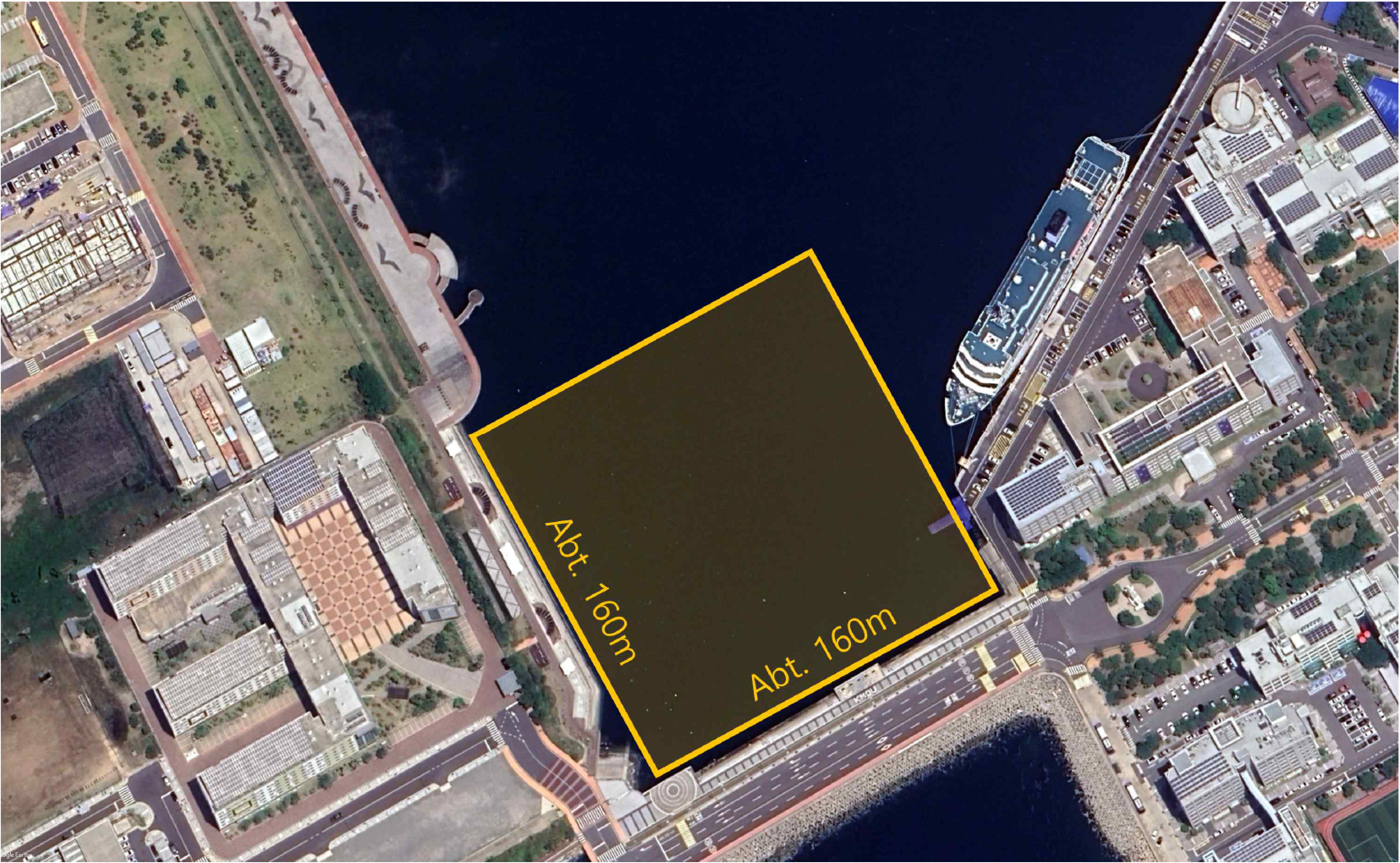
Turning Experiments were conducted twice to identify and verify ship dynamic model parameters, and tune PD control parameters. The motor rpm was kept constant, and various rudder angles were used to obtain rate of turn data. The data sampling interval is 1 second. The first experimental data was used to identify ship dynamic model parameters, and the second experimental data was used to verify the identified model. The experimental area is open to the north, as shown in Fig. 4. During the experiments, the wave height was maintained at 0.3 m or less and the wind speed was maintained at 1.8 m/s or less.
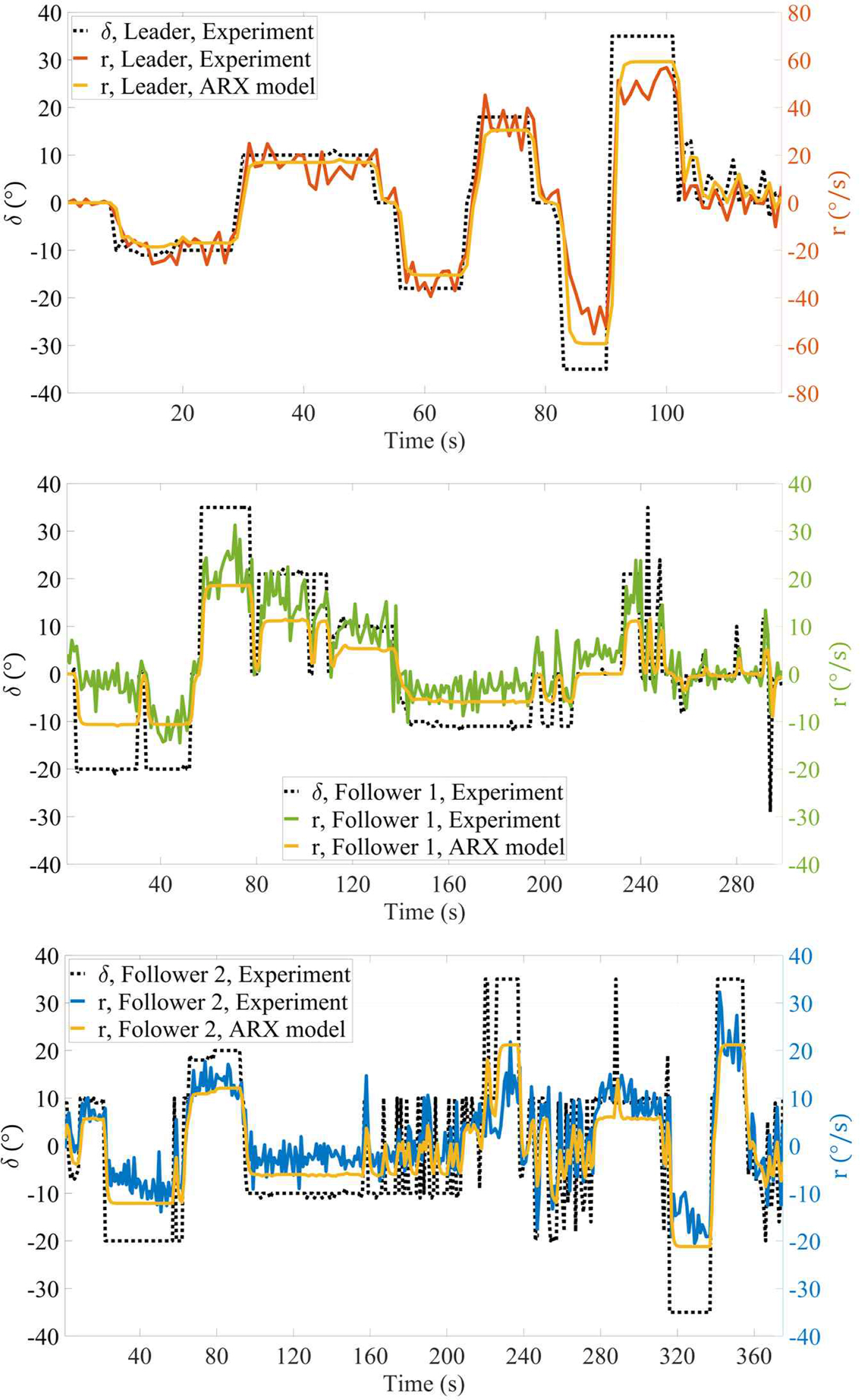
Fig. 5 shows the rudder angle and rate of turn of each boat in the first turning experiment. The black dashed line represents the rudder angle, and the red, green and blue solid lines represent the rate of turn of each boat. Leader had twice the rate of turn compared to Followers at the same rudder angle. The maximum rates of turn at the maximum rudder angle were 63.9°/s for Leader, 30.4°/s for Follower 1 and 32.1°/s for Follower 2. And even if the rudder angle was kept constant, the turn rate oscillated. This is considered to be because the experimental boats react sensitively to marine environmental factors.
The ARX model parameters were identified using the data of rudder angle and rate of turn by the MATLAB System Identification Toolbox. Transfer functions for the dynamic models of Leader (GL (z)), Follower 1 (GF1(z)), and Follower 2 (GF2(z)), which show the relationship between the rate of turn and the input rudder angle, are given in Equations (11) to (13).
Fig. 6 shows the rudder angle and rate of turn obtained by second turning experiment and ARX model. The yellow solid lines represent the rate of turn calculated by ARX model of each boat. The root mean square error (RMSE) which represents the difference between the values by the ARX model and the experiments were 7.4°/s for Leader, 5.0°/s for Follower 1 and 4.9°/s for Follower 2. Considering that the rate of turn data from the turning experiment oscillates due to external environmental factors, the identified ARX models are suitable for representing the ship dynamic model of each experimental boat.
Using the dynamic models of the experimental boats, the PD control parameters were tuned to minimize overshoot and prevent excessive use of the rudder. Parameter tuning was performed using MATLAB Simulink and the control parameters were KP = 0.2 and KD = 0.4 for Leader, and KP = 0.4 and KD = 0.8 for Followers.
3.3 Verification experiment
Sea experiments were conducted to verify the proposed algorithm. The FSD was set to 12.2 m, and the target speed was set to 1.5 m/s. Table 2 lists the predetermined waypoint, course and distance. The courses were set to change about 50° to starboard at each waypoint, and the distance between waypoints was about 50 m. The experiment was conducted five times, and almost similar results were obtained each time. During the experiments, the wave height was maintained at 0.3 m or less and the wind speed was maintained at 1.7 m/s or less.
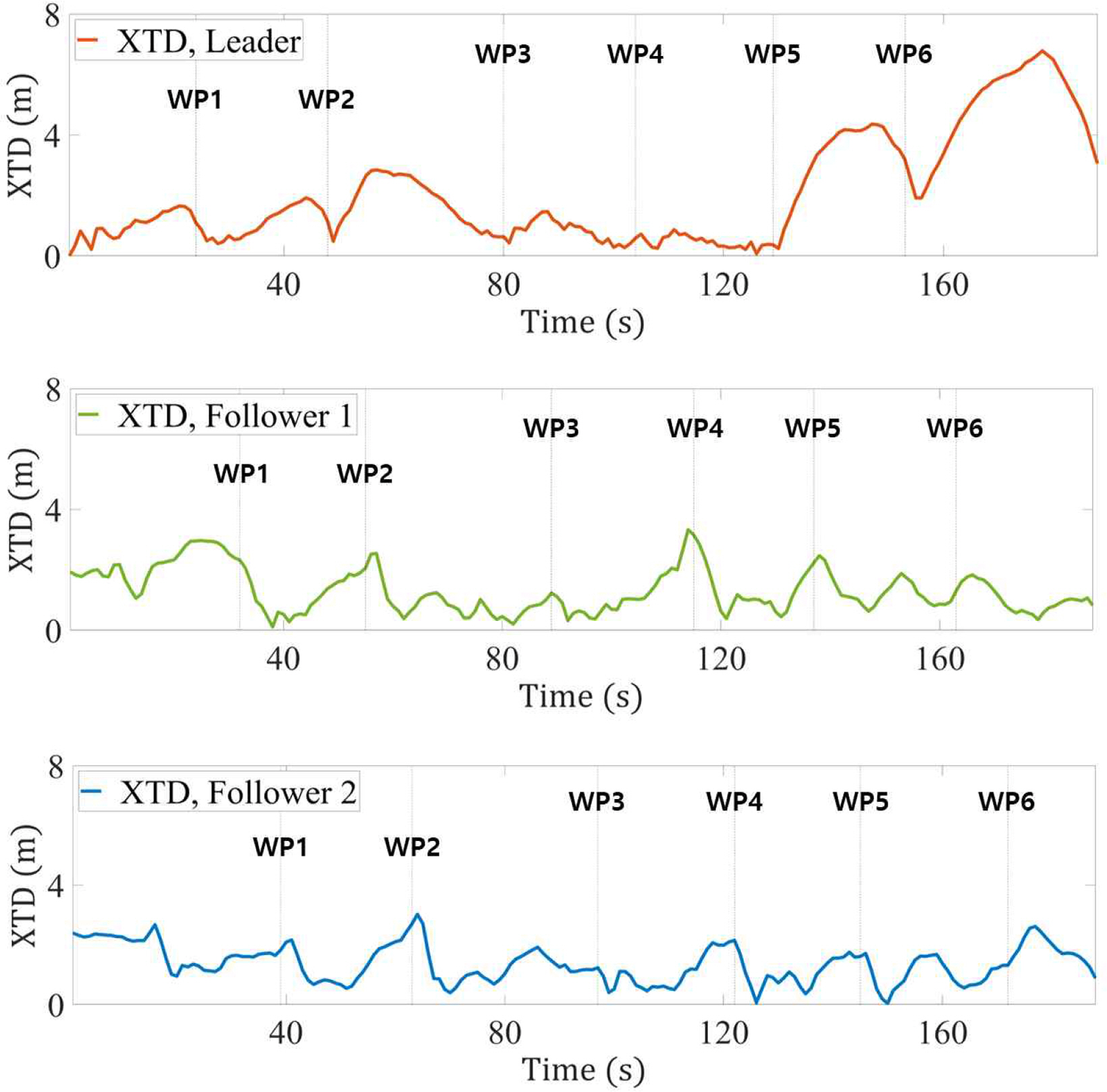
Fig. 7 shows the entire trajectories of the three boats, and waypoints are indicated by star markers. Fig. 8 shows the XTD (Cross Track Distance) of each boat, and vertical lines represent when each boat passed through waypoints from 1 to 6. Here, XTD refers to the distance of deviation for Leader from the planned route or for Follower from the trajectory of Leader. As shown in Fig. 7 and 8, Leader navigated on the planned route and Followers also followed the trajectory of Leader well. From WP 5 to WP 6 and until the end point, Leader deviated from the planned route by about 6.8 m due to external influences. And Followers followed only the deviated trajectory of Leader. Fig. 9 shows the sea experiment scene and it can be seen that Followers followed Leader well.
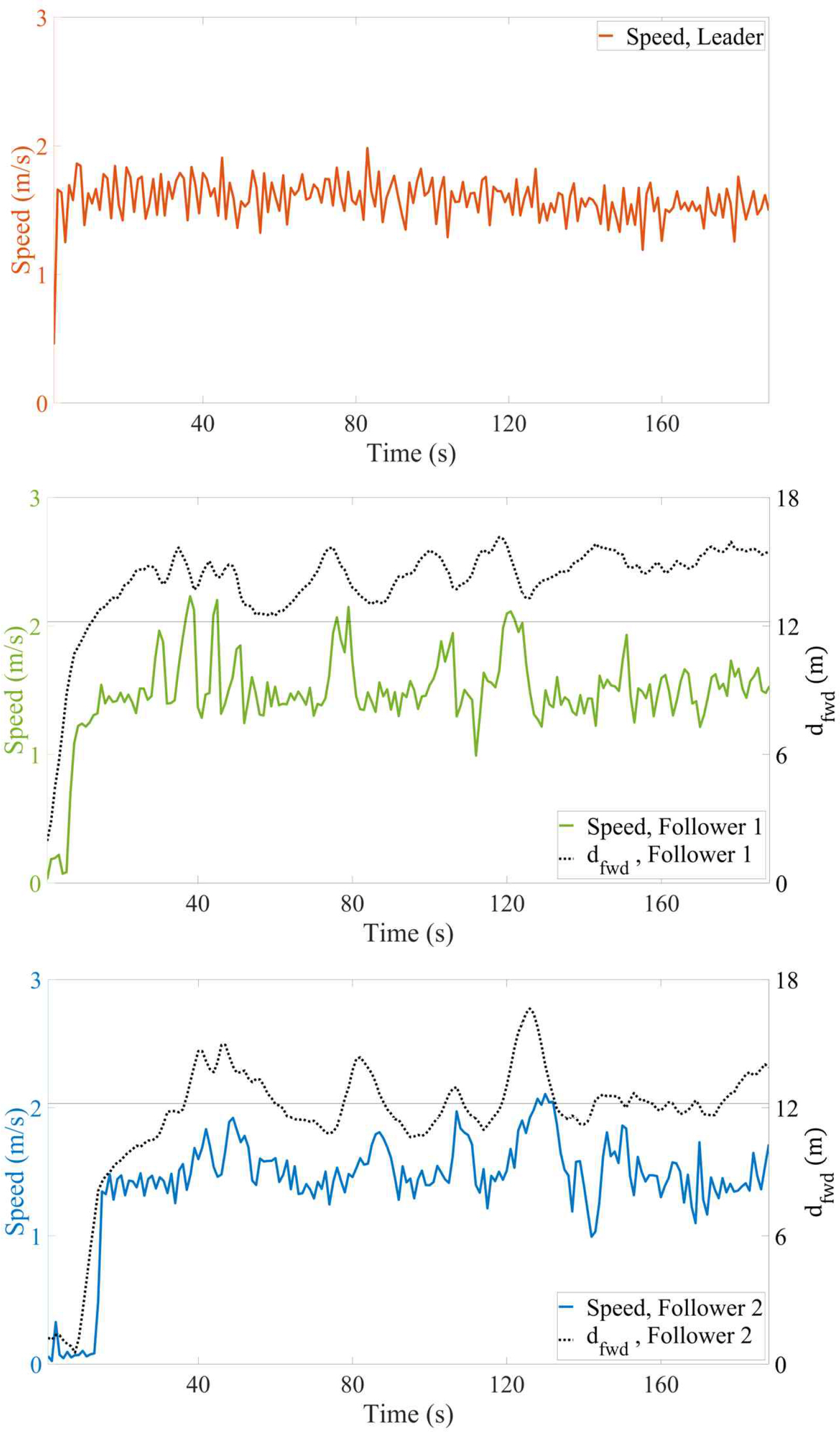
Fig. 10 shows the speed, and distance to the forward boat. The black dashed line represents the distance to the forward boat, and the red, green and blue solid lines represent the speed of each boat. The speed of Leader was oscillated continuously, despite maintaining a constant motor speed. This is considered to be due to the fact that the boat is small and light, making it vulnerable to external influences. Its average speed was 1.59 m/s, a maximum speed of 1.98 m/s and a minimum speed of 1.19 m/s. Follower 1 maintained a distance of 12.3∼16.1 m from Leader. Its average speed was 1.53 m/s, a maximum speed of 2.23 m/s and a minimum speed of 0.99 m/s. Follower 2 maintained a distance of 10.6∼16.6 m from the Follower 1. Its average speed was 1.52 m/s, a maximum speed of 2.11 m/s and a minimum speed of 0.99 m/s.
4. Conclusions
This study presents the implementation of the ship trajectory following algorithm that enables followers follow the trajectory of the leader. The algorithm was verified through sea experiments using 1 m class RC model boats. The results are as follows.
Firstly, Followers closely followed the trajectory of Leader. The maximum XTD of Followers were about 3 m. Even if Leader deviated from the planned route, Followers still followed only the trajectory of Leader.
Secondly, the experimental boats maintained a distance each other to prevent collision. Follower 1 maintained a distance from the Leader within the range of 101∼132% of the forward safe distance of 12.2 m. Follower 2 maintained a distance from the Follower 1 within the range of 87∼ 136% of the forward safe distance of 12.2 m.
The study focused on verifying ship trajectory algorithms using 1 m class small model boats. While this algorithm designed for three boats navigating in a straight line, the group shape needs to be adjusted based on the number of ships and navigational circumstances. When the number of ships increases, the group shape should be two or more columns. As its basic shape is a triangular, authors plan to develop algorithms and conduct sea experiments to form a triangular shape in future research.