심해공학수조 조파기 전달함수 근사 모델 개발
Development of Meta Model of Transfer Function for Wavemaker of Deep Ocean Engineering Basin
Article information
Abstract
본 연구는 심해공학수조의 파 생성 특성을 규명하고, 심해공학수조의 기하학적 특성을 반영한 조파기 전달함수의 근사모델을 개발하는 것을 목적으로 한다. 심해공학수조의 기하학적 특성을 반영한 효율적인 해석을 위해 2차원 주파수영역 경계요소법이 적용되었다. 개발된 수치해석법은 해석해와 비교하여 검증되었다. 다양한 주기와 이동식 바닥판의 위치 변화에 대한 조파기의 경계치 문제의 수치해석이 수행되었다. 수치결과를 통해 심해공학수조의 기하학적 특성이 조파기의 전달함수에 미치는 영향을 조사하였고, 이동식 바닥판의 위치를 변화시켜 파도 생성에 대한 깊이 효과를 확인하였다. 경계요소법의 다양한 결과를 효율적으로 활용하기 위해 박판 스플라인 보간 모델 기반의 조파기 근사모델을 개발하였다. 개발된 근사 모델의 타당성은 모델 테스트 결과 비교를 통해 확인하였다.
Trans Abstract
This study aims to investigate the characteristics of wave generation in a deep ocean engineering basin and to develop a meta-model of the transfer function of the wavemaker that reflects the geometric characteristics of the deep ocean engineering basin. To this end, the two-dimensional frequency domain boundary element method was applied to achieve an efficient analysis that reflects the geometric characteristics of the deep ocean engineering basin. The developed numerical method was validated through comparison with the analytical solution. Numerical analyses were conducted for the boundary value problem of the wavemaker according to various periods and the positions of the movable bottom. The numerical results were used to investigate the effect of the geometric characteristics of the deep ocean engineering basin on the transfer function of the wavemaker, and the effect of depth on wave generation was checked by changing the position of the movable bottom. To efficiently utilize the various results of the boundary element method, a meta-model, an approximate model of the transfer function of the wave maker, was developed using a thin plate spline interpolation model. The validity of the developed meta-model was confirmed through a comparison of the results of the model tests.
1. 서 론
해상에서 운용되는 선박 또는 구조물의 정도 높은 설계를 위하여 파랑에 기인한 구조물의 거동 평가는 필수적이다. 설계 시 파랑에 기인한 구조물의 거동 평가를 위하여 포텐셜 유동에 기반한 수치해석(Jung et al., 2021)이 널리 수행되고 있으나 최종 설계의 검증으로 모형시험이 아직도 신뢰되고 있다(Jung et al., 2020). 신뢰성 있는 파랑 중 모형시험을 위해서 정밀한 파 생성은 필수적이다. 정밀한 파를 생성하기 위해서는 수조의 기하학적 형상을 고려한 파 생성 특성은 물론 정확한 조파기의 전달함수를 파악하는 것이 가장 기본이다.
조파기 이론은 Havelock(1929)의 연구를 시작으로 Biésel and Squet(1951)에 의해 피스톤 또는 플랩 형태의 조파기의 전달함수가 최초로 도출되었다. 이후 Flick and Guza(1980), Hudspeth and Sulisz(1991), Moubayed and Williams(1994) 그리고 Schäffer(1996)에 의해 2차 오더의 파 생성이론이 개발되었다. 3차원 수조의 파랑 생성에 대한 연구(Dalymple and Dean, 1972; Madsen, 1974) 또한 활발히 진행되었다. 국내에서는 An et al.(2013)의 2차원 수조시험 연구는 물론 Kwon et al.(2017)의 조파기의 근사이론식 개발 등 다양한 연구가 진행되고 있다. 일반적으로 상기 연구의 이론들에 기초하여 조파수조의 파를 생성하지만 조파기의 종류 및 수조의 기하학적인 특성 또는 제원에 따라 다양한 조파특성이 나타나므로 관련된 연구가 필요하다.
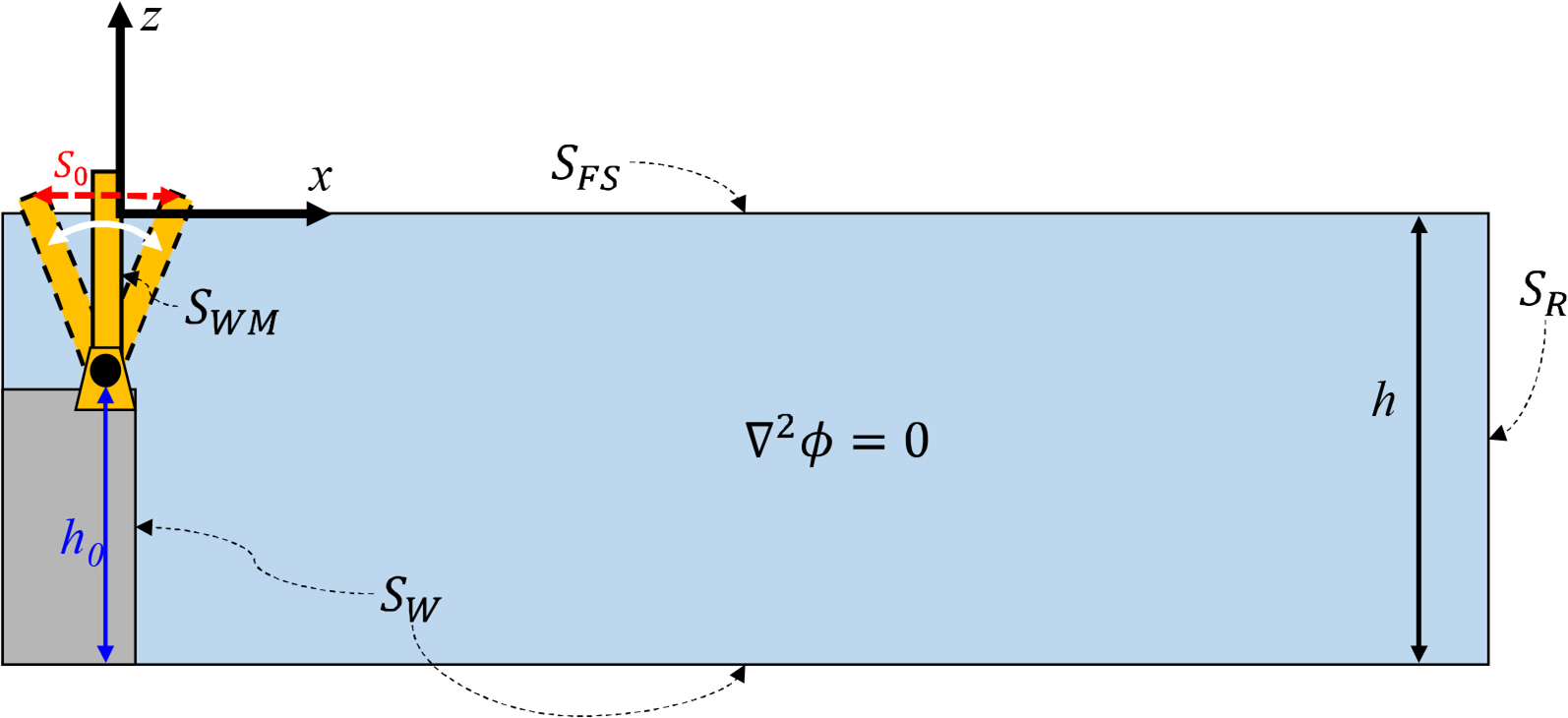
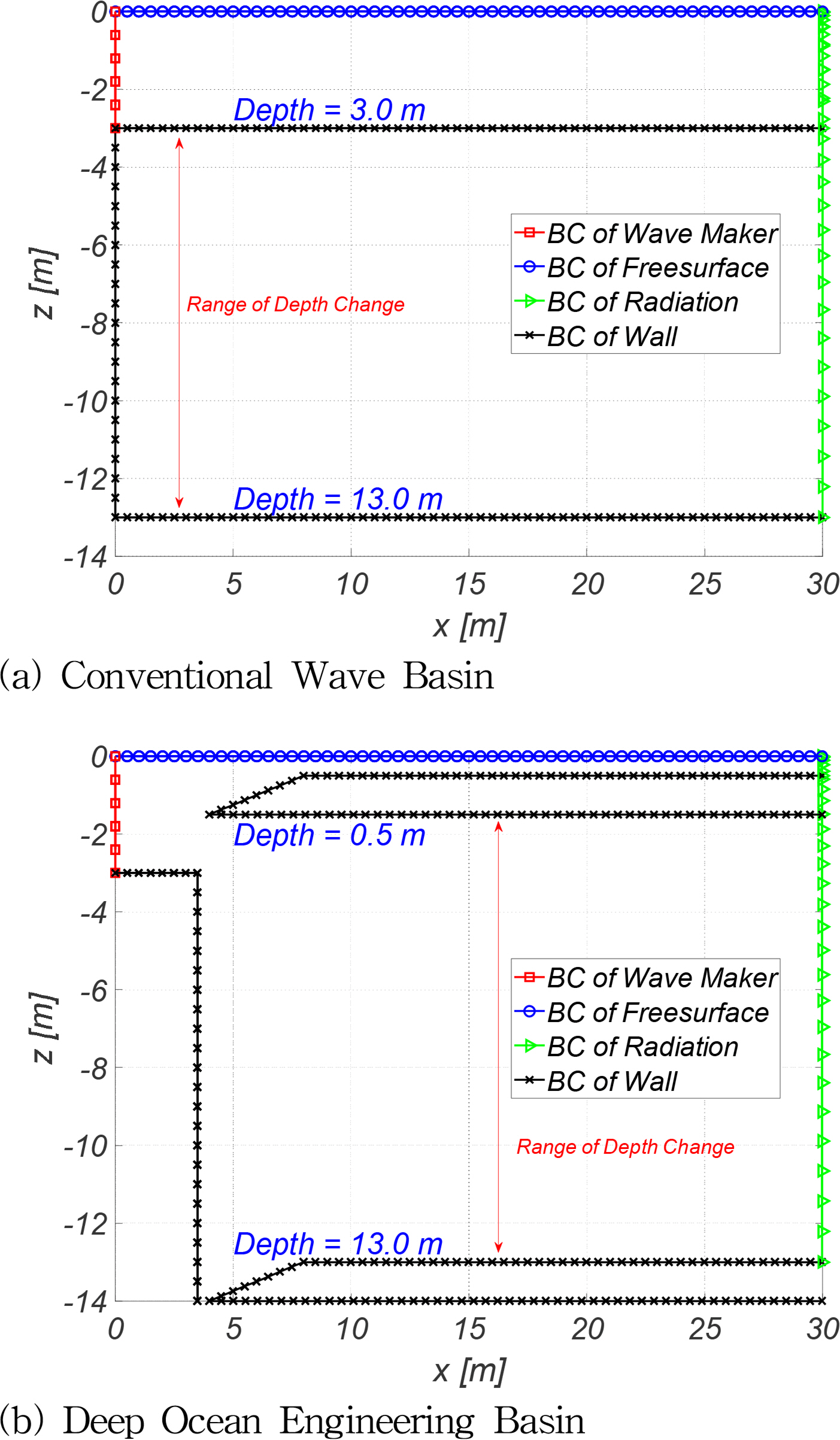
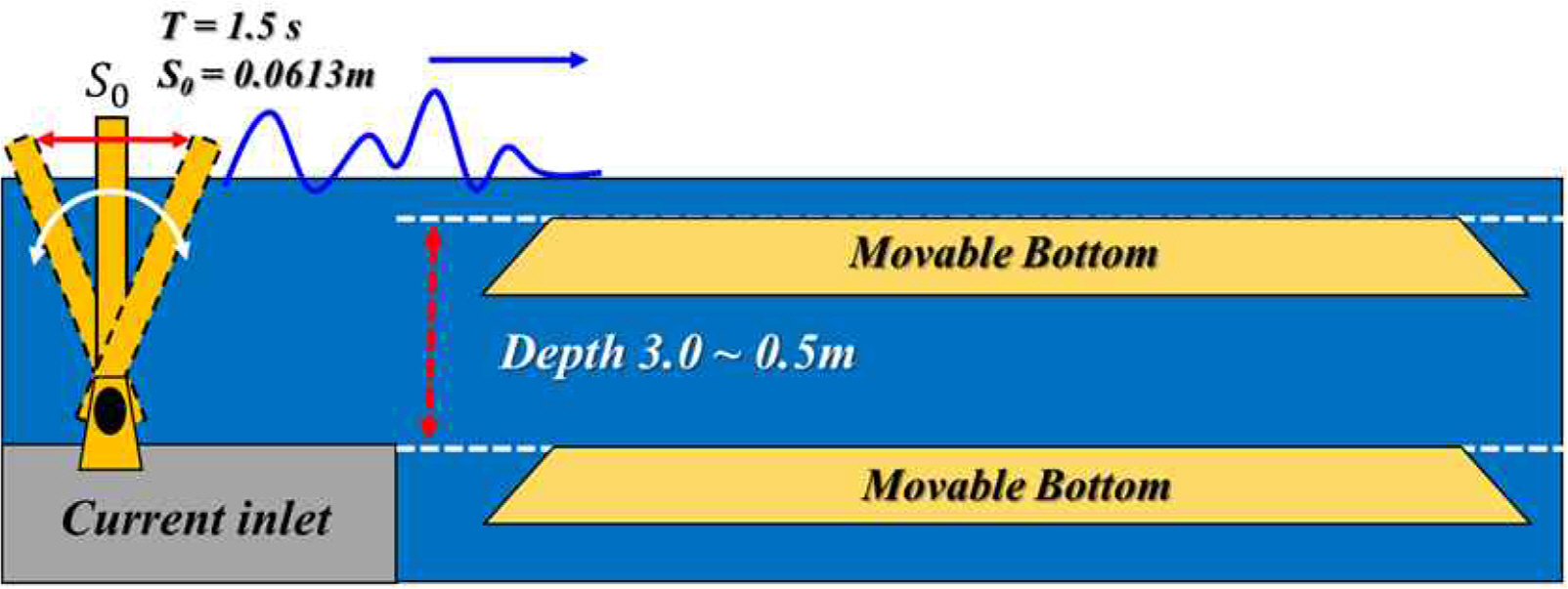
현재 해양과학기술원 부설 선박해양플랜트연구소(Korea Research Institute of Ships and Ocean Engineering, KRISO)에서는 심해공학수조(Deepwater Ocean Engineering Basin, DOEB)가 건설 되어 다양한 선박과 해양구조물의 파랑 중 성능평가 모형시험이 수행되고 있다. 따라서 효율적이고 정밀한 모형시험을 위해 심해공학수조의 조파 특성이 조사되어야 한다. 심해공학수조에는 elevated flap 형의 조파기가 설치되어 있다. 일반적인 수조의 조파기는 Fig. 1(a)과 같이 설치되어 있고 Biésel and Suquet(1951)에 의해 도출된 해석해가 존재한다. 하지만 심해공학수조에는 Fig. 1(b)와 같이 조류 유출구와 같은 계단지형과 이동식 바닥판에 기인한 기하학적 특성이 존재한다.
특히 이동식 바닥판은 상하로 이동 가능하여 수심 조절의 역할을 하도록 고안되어 있기 때문에 해당성능 검증은 물론 기하학적 특징이 조파기 전달함수에 미치는 영향을 확인해야 한다. 그리고 이동식 바닥판이 조파기 힌지보다 높이방향으로 위에 위치하고 있는 경우, 알려진 이론해가 존재하지 않기 때문에 이에 대한 수치해를 확보하는 것 또한 필요하다. 조파기 전달함수를 이용할 때 매 순간 경계치 문제를 푸는 것은 비효율적다. 따라서 도출된 전달함수를 효율적으로 근사할 수 있는 근사모델의 확보도 요구된다.
본 연구에서는 심해공학수조의 파랑생성 특성을 규명하고 기하학적 특성이 반영된 조파기 전달함수의 근사모델 개발을 목표로 한다. 심해공학수조의 기하학적 형상을 반영한 효율적인 해석을 위해 2차원 주파수영역 경계요소법이 적용되었다. Biésel and Suquet(1951)의 해석해와 비교하여 개발된 수치해법을 검증하였다. 다양한 주기와 이동식 바닥판의 위치에 따른 조파기의 경계치 문제에 대한 수치해석을 수행하였다. 수치결과를 통하여 심해공학수조의 기하학적 특성이 조파기전달함수에 미치는 영향을 조사하였고 이동식 바닥판의 위치의변화로 인한 조파 시 수심효과를 확인하였다. 경계요소법의다양한 결과를 효율적으로 활용하기 위해 thin plate spline 보간모델을 이용한 조파기 전달함수의 근사모델을 개발하였다. 모형시험과 비교를 통하여 개발된 근사모델의 유효성을 확인하였다.
2. 수학적 정식화 및 수치기법
2.1 수학적 정식화
본 연구에서는 Fig. 2와 같이 2차원 직교 좌표계(x, z)를 사용하였고 z는 평균수면을 기준으로 상방을 향한다.
유체의 비압축과 비점성 그리고 유동의 비회전성을 가정하면 유체속도는 속도포텐셜 ϕ의 구배로 표현 가능하고 유체 연속방정식은 식 (1)과 같은 라플라스 방정식으로 나타난다.
유체의 경계를 자유수면경계 SF, 조파경계 SWM, 방사경계 SR 그리고 벽경계 SW 조건으로 구성하여 Fig. 2와 같이 조파기 문제의 경계치 문제를 구성할 수 있다. 자유수면 경계조건은 선형화된 통합 자유표면 경계조건으로 식 (2)와 같다.
여기서 ω는 각주파수 그리고 g는 중력가속도를 의미한다. 조파기의 변위를 통하여 조파기의 경계조건을 식 (3)과 같이 기술할 수 있다.
본 연구에서 고려되는 elevated flap형 조파기 운동은 고정된 힌지를 중심으로 운동한다. 따라서 조파기의 변위 S는 식 (4)와 같이 일반화 될 수 있다.
여기서 S0는 조파기 스트로크, H는 수심 그리고 H0는 수조바닥에서 조파기 힌지까지의 높이를 의미한다.
원방으로 파가 전파되는 방사조건을 식 (5)와 같이 나타낼 수 있다.
여기서 k는 방사되는 파의 파수(wave number)를 의미한다.
그 외의 벽면, 바닥 또는 이동식 바닥판과 같이 유체가 수직으로 통과하지 못하는 경계에는 불 투과성 경계조건인 식 (6)으로 나타낼 수 있다.
경계치 문제의 해를 구하면 동역학적 자유수면 조건을 이용하여 자유수면의 높이를 식 (7)과 같이 나타낼 수 있다.
조파기의 전달함수는 조파기 경계면에 부여된 조파기의 변위 S와 원방의 파고 H의 관계를 통해 식 (8)과 같이 나타낼 수 있다.
2.2 수치기법
주어진 경계치 문제를 풀기위해 경계요소법의 일종인 간접경계적분방정식을 이용하였다. 해당 방법은 기본해인 식 (9)와 간접경계적분방정식 (10)을 이용한다(Oh et al., 2018).
여기서 소오스
식 (11)을 경계조건 식 (2), (3), (5) 그리고 (6)에 대입하여 연립방정식을 구성할 수 있다. 구성된 연립방정식을 이용하여 밀도함수 σ를 결정할 수 있으며 결정된 밀도함수 σ와 식(11)을 이용하여 경계표면의 potential ϕ를 계산할 수 있다.
3. 수치계산 및 결과
3.1 수조제원과 계산격자 구성
심해공학수조는 Table 1과 같은 제원을 가지고 있으며 조파기는 0.5초에서 5초 주기의 파를 생성할 수 있다. 본 연구에서는 이동식 바닥판의 운영조건을 고려하여 13.0m ~ 0.5m 수심 범위에서 대하여 연구를 수행하였다.
본 연구에서는 식(12)와 같이 해석해(Biésel and Suquet, 1951)가 존재하는 elevated flap 조파기 경계치 문제(이하 CWB BVP; Conventional Wave Basin Boundary Value Problem)와 비교를 통하여 심해공학수조의 기하학적 형상이 조파기 전달함수에 미치는 영향을 관찰하고자 한다.
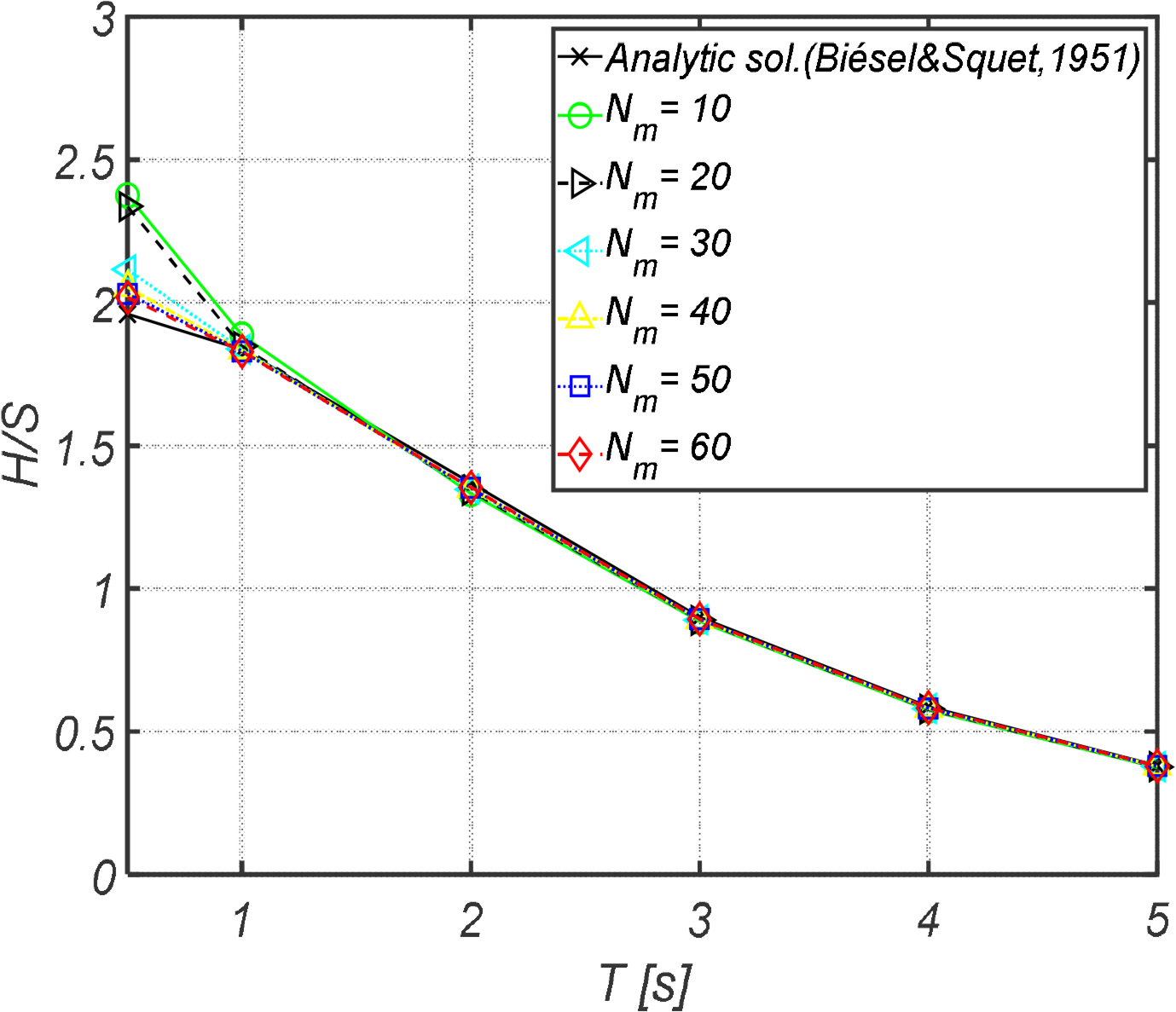
따라서 Fig. 3과 같이 각각의 문제에 대하여 2차원 격자를 구성하였다. 조파기, 자유수면 그리고 벽 경계조건의 격자는 균일하게 분포하였고 방사경계면은 자유수면에 가까워지면 격자가 밀집되도록 cosine 분포로 격자를 구성하였다. 수심변화에 대한 많은 경계치 문제의 계산을 위해 격자 자동생성 알고리즘을 고안하였다. 심해공학수조의 길이는 100m이나, 계산의 효율을 위해 5초의 주기 파장의 결과가 수렴되는 길이 30m를 설정하였다. 해당 길이는 반복 계산을 통해 도출되었다. 최소 격자 사이즈는 0.5초 주기의 파장을 근거로 결정하였다. 0.5초 주기의 파장에 대하여 10, 20, 30, 40, 50 그리고 60개의 요소를 가지도록 Fig. 3(a)의 13m 깊이에 대한 격자를 구성하여 수렴도 시험을 수행하였고 결과를 Fig. 4에 도시하였다. 0.5초 주기의 파장 기준으로 60개의 요소를 가지면 대부분의 주기에서 수렴된 결과를 가지는 것을 확인할 수 있다.
3.2 심해공학수의 조파기 전달함수 도출 및 조파 특성 파악
CWB BVP와 심해공학수조의 기하학적 형상을 반영한 경계치 문제(이하 DOEB BVP; Deep Ocean Engineering Basin Boundary Value Problem)에 대한 조파기 전달함수를 도출하기 위하여 Table 2와 같은 조건에 대하여 계산을 수행하였다.
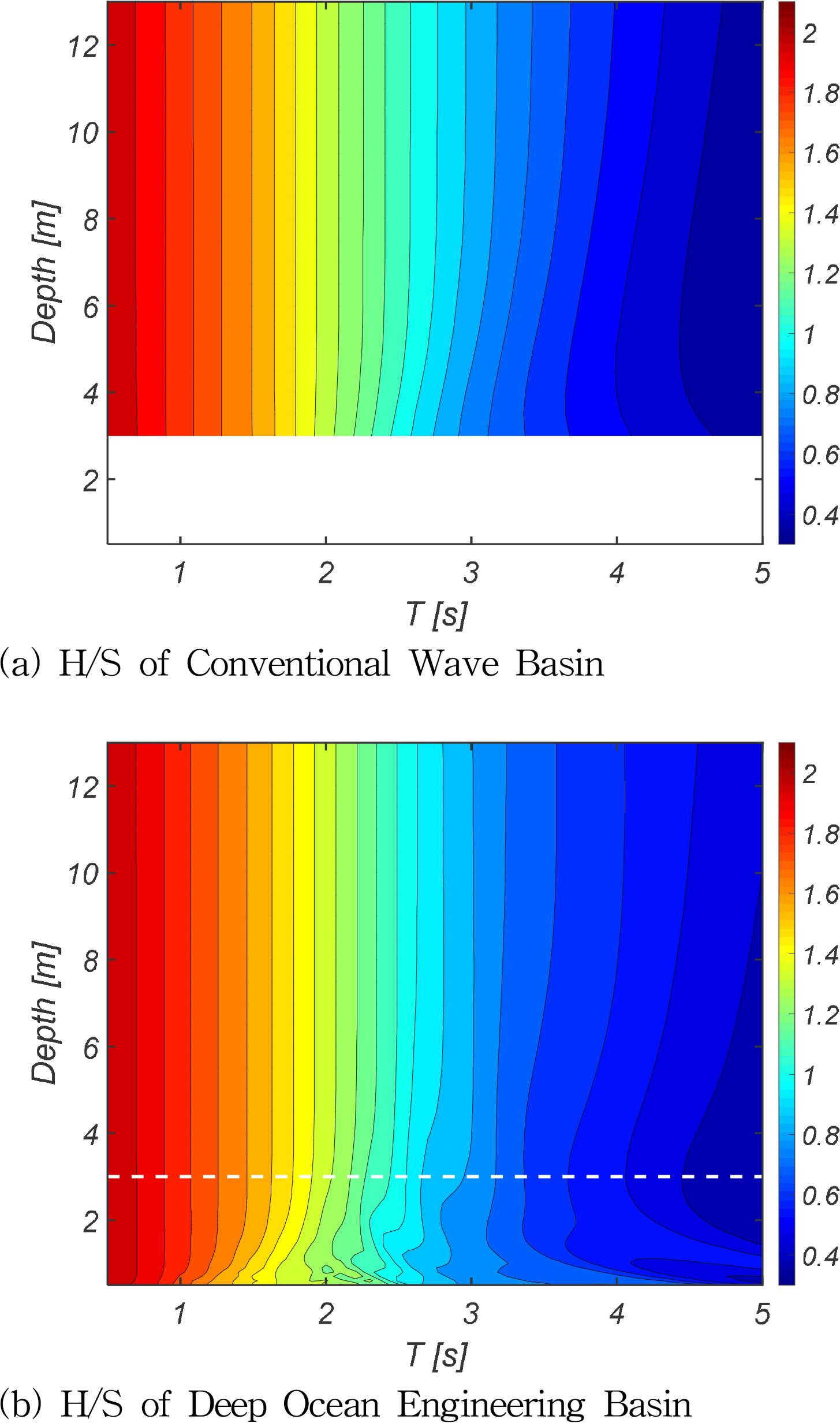
파의 주기는 조파기의 성능을 참조하여 선정하였으며 수심의 경우는 심해공학수조의 운용조건을 고려하여 선정하였다. 비교를 위한 CWB BVP의 경우, 힌지가 위치한 수심인 3.0m까지 계산을 수행하였다. 계산된 각각의 경계치 문제는 총 3082cases이다. 계산에서 도출된 조파기 전달함수는 Fig. 5와 같이 도시하였다.
조파기 전달함수를 살펴보면 수심 3.0m 이상, 주기 2.0초 이하에서 두 조파기 전달함수가 거의 동일함을 알 수 있다.
이는 주기 2.0초 이하의 파장이 약 6m 이하로 파랑의 속도장이 수심 3.0m 이하로 존재하기 때문에 해당 기하학적 특성에 영향을 받지 않음을 추론할 수 있다.
조류 유출구와 같은 계단지형과 이동식 바닥판이 조파기 전달함수에 미치는 영향을 더욱 면밀히 관찰하기 위하여 수심별 전달함수를 Fig. 6에 도시하였다. Fig. 6(a)는 수심 3.0m로 이동식 바닥판의 상부가 조류 유출구의 상부의 높이가 동일하지만 주기 2.6 ~ 3.4 초 사이에서 전달함수의 차이가 발생한다. 이는 이동식 바닥판과 조류 유출구 사이의 갭에 기인한 영향으로 판단된다. 수심이 깊어짐에 따라 주기 2.3 ~ 5초 사이의 넓은 범위에 전달함수 차이가 발생되는 것을 관찰할 수 있다. 이러한 차이는 이동식 바닥판이 하강함에 따라 조류 유출구가 계단지형과 같은 기하학적 특성이 반영된 것으로 판단된다. 전반적으로 계단지형의 효과는 있으나 영향은 미미하며 이동식 바닥판이 수심효과를 잘 고려하는 것을 확인할 수 있다.
조류 유출구와 같은 계단지형과 이동식 바닥판이 파의 공간적 특성에 미치는 영향을 파악하기 위하여 normalize elevation과 normalize amplitude를 식 (13)–(14)와 같이 정의하였다. normalize elevation과 normalize amplitude는 조파기로부터 거리에 대한 함수로 도출되기 때문에 공간특성 파악에 용이하다.
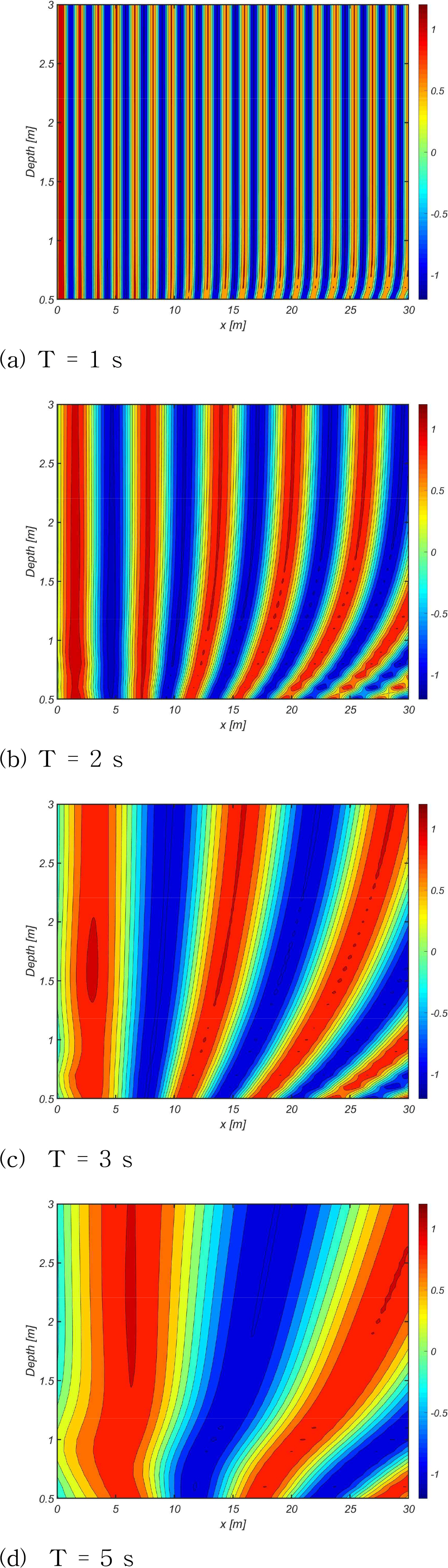
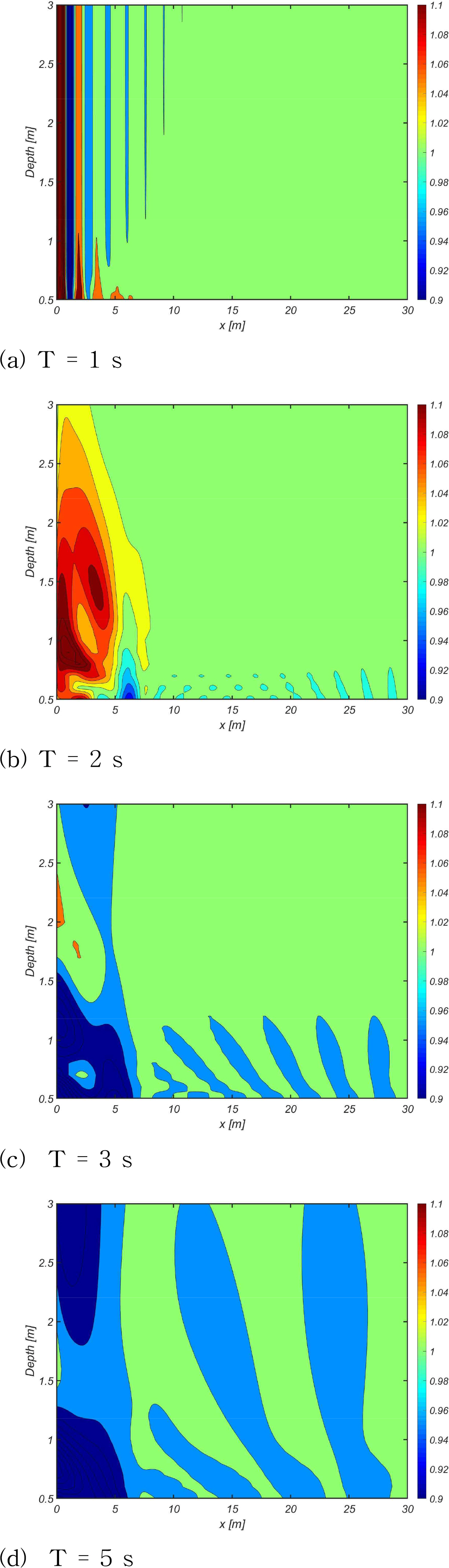
조류 유출구의 수심을 고려하여 파장 6m을 경계로 1.5초 와 3.5초 두 주기의 파를 선정하였다. 해당 파들의 공간적 특성을 관찰하고 계단지형의 영향을 확인하였다. Fig. 7은 주기 1.5초의 파 조건에서 수심변화에 대한 normalize elevation과 normalize amplitude를 등고선으로 나타내었다. 주기 1.5초 파의 경우, 속도장이 수심 3m 이하로 존재하기 때문에 CWB BVP와 DOEB BVP의 normalize elevation이 수심에 변화와 무관하게 동일함을 Fig. 7(a)에서 관찰할 수 있다. 그리고 normalize amplitude를 통하여 조파기로부터 10m 이내의 evanescent mode의 파 진폭이 거의 유사하게 관찰되며 이후 파 진폭이 수렴됨을 Fig. 7(b)에서 확인할 수 있다.
주기 3.5초의 파 조건 또한 Fig. 8과 같이 수심변화에 대한 normalize elevation과 normalize amplitude를 등고선으로 나타내었다. 주기 3.5초 파의 경우, CWB BVP와 DOEB BVP 모두 수심이 감소함에 따라 파장이 감소함을 Fig. 8(a)에서 관찰할 수 있다.
그리고 주기 1.5초와 달리 수심이 깊어질수록 두 문제의 파의 위상차가 발생함을 확인할 수 있다. 이를 좀 더 명확하게 나타내기 위하여 Fig. 9에 수심 별 normalize elevation을 도시하였다. 이러한 위상차는 3m 수심의 파장이 계단지형으로 수심이 깊어짐에 따라 파장이 길어지고 파의 위상속도가 증가하기 때문으로 추정할 수 있다.
그리고 normalize amplitude를 통하여 조파기 근처에서 두 경계치 문제의 evanescent mode의 파 진폭의 차이를 Fig. 8(b)에서 관찰할 수 있다. 따라서 조파기 근처의 evanescent mode의 파 진폭의 차이는 DOEB의 조류 유출구와 같은 계단지형에 기인한 기하학적 특성으로 판단된다. DOEB의 경우, 수심에 따라 파의 evanescent mode가 사라지는 구간이 20m 이후로 확인되며 모형시험 시 이를 고려하여 수행되어야 할 것이다.
이동식 바닥판의 위치가 수심으로 3m 이하에 위치할 경우, 이동식 바닥판이 수심 변화 효과는 물론 수중 장애물의 효과도 예상된다. 해당 영역에서 조파 특성을 파악하기 위하여 수심변화에 대한 normalize elevation을 Fig. 10에 도시하였다. 이동식 바닥판의 깊이가 감소함에 따라 파장이 감소하는 것을 확인되며 이는 이동식 바닥판이 수심변화 효과를 구현할 수 있음을 의미한다.
수심변화에 대한 normalize amplitude을 Fig. 11에 도시하였다.
주기가 길어짐에 따라 이동식 바닥판의 깊이가 낮은 영역에서 파 진폭이 수렴되지 않음을 확인할 수 있다. 이는 파장이 길어짐에 따라 이동식 바닥판이 수중 장애물의 효과가 커짐을 의미하며 해당구간의 시험 가능유무를 판단하기 위해서는 비선형 파랑해석(Oh et al., 2018; Oh et al., 2020) 또는 모형시험을 통한 이동식 바닥판의 반사 또는 산란효과의 면밀한 검토가 필요하다.
4. 심해공학수조 조파기 전달함수 근사모델
모형수조에서 목표한 파를 구현하기 위해서는 조파기의 전달함수가 필수적이다. 심해공학수조의 기하학적 특성을 반영한 전달함수를 도출하기 위하여 매 순간 경계치 문제를 푸는 것은 비효율적이다. 따라서 조파기 전달함수를 대체할 수 있는 근사모델의 개발이 필요하다. 이러한 근사모델은 회귀모델과 보간모델로 구분된다. 회귀모델의 경우, 데이터의 노이즈 제거 효과가 있기 때문에 랜덤에러가 있는 시험데이터에 적합하며 보간모델의 경우 랜덤에러가 없는 수치계산에 적합하다. 본 연구에서는 radial basis function을 활용한 thin plate spline interpolation model(TPS model)을 통하여 심해공학수조의 조파기 전달함수의 근사모델을 개발하였다.
4.1 Thin plate spline interpolation model
TPS model은 방사기저함수
일반적으로 방사기저함수 외
본 연구에서는 경계요소법으로 도출한 2116개의 전달함수 데이터를 활용하여 식 (16)의 선형계수 θ와 비선형계수 λ를 Table 3에 도출하였다.
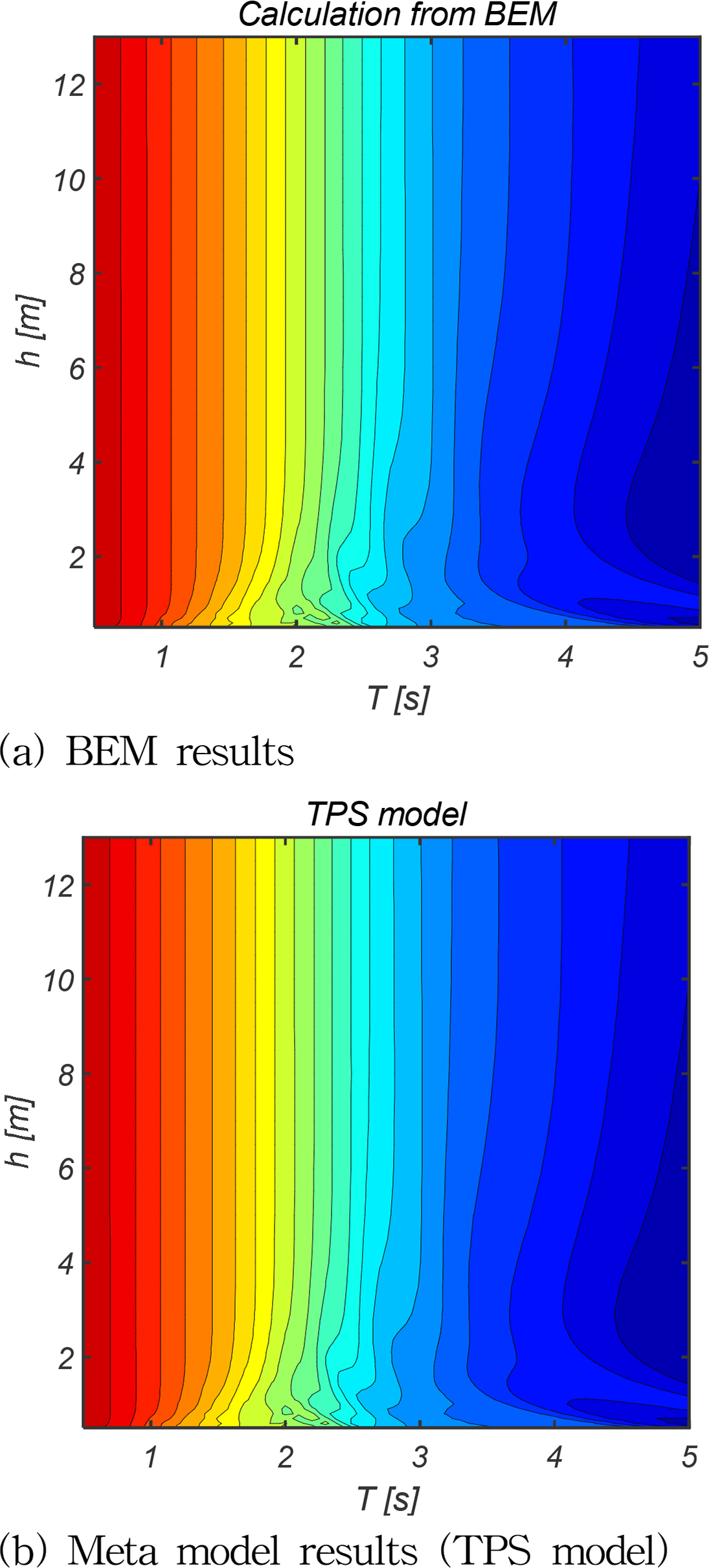
도출된 파라메터를 식 (16) 대입하면 심해공학수조 조파기의 전달함수를 원하는 수심과 주기에서 Fig. 12와 같이 도출할 수 있다.
Fig. 12에서 해당모델과 경계요소법으로 도출된 총 2116개의 데이터가 거의 동일함을 알 수 있다. 해당 모델의 정확성을 면밀히 확인하기 위하여 식 (17)과 경계요소법으로 도출된 총 2116개의 데이터를 이용하여 오차를 평가하였다. 해당 오차는 9.2815e-24로 근사모델(TPS model)과 경계요소법의 결과가 완전히 일치함을 확인하였다.
4.2 모형시험을 통한 근사모델 검증
본 연구에서 개발된 근사모델을 검증하기 위하여 모형시험 결과와 비교를 수행하였다. 모형시험은 Fig. 13과 같이 일정한 조파기 stroke와 주기에서 이동식 바닥판의 수심 변화에 따른 파를 계측하였고 시험조건은 Table 4와 같다.
모형시험은 심해공학수조에서 수행되었으며 파고 계측을 위해 9개의 용량식 파고계(capacitance type wave probe)를 Fig. 14와 같이 배치하여 수행되었다.
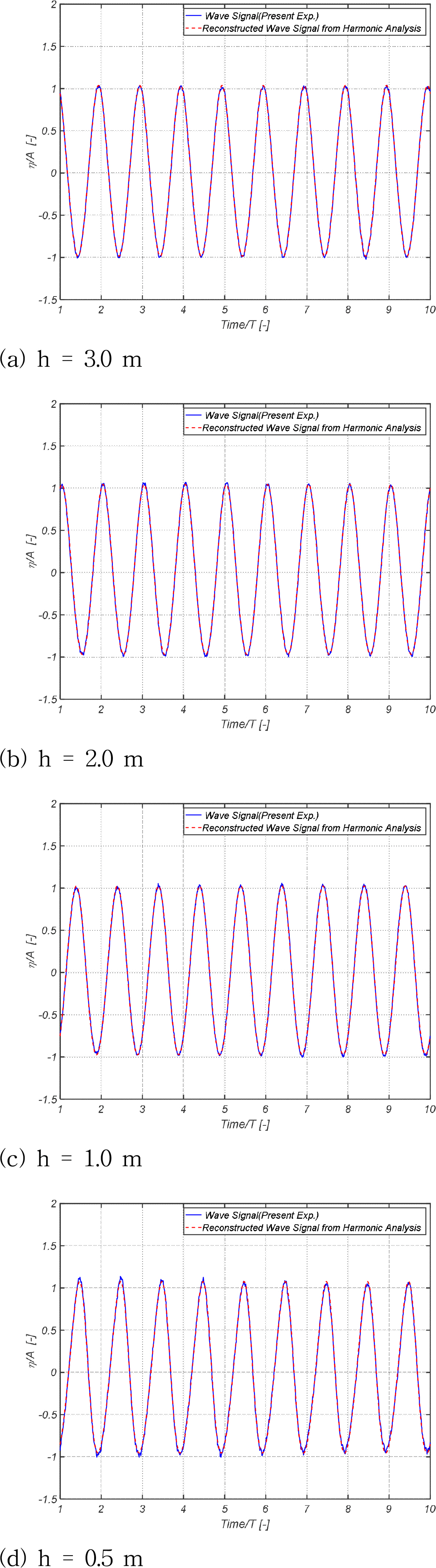
계측신호를 수집하기 위한 데이터수집장치로 National Instruments사의 cDAQ가 사용되었다. 데이터는 100 Hz로 수집되었다. 계측된 신호는 Fig. 15와 같이 조화해석을 통하여 파 진폭이 해석되었다.
해당 시험을 통하여 이동식 바닥판의 낮은 수심에서도 규칙파가 잘 생성됨을 확인할 수 있다.
계측 결과로부터 모형시험에서 관찰된 파 진폭을 이용하여 조파기 전달함수를 도출하였고 근사모델과 비교하여 Fig. 16(a)에 도시하였다. 해당 비교를 통하여 수심 1m 이상에서는 5% 이하의 오차가 확인되며 해당 근사모델의 타당성을 확인하였다. 수심 0.5m에서는 근사모델보다 모형시험의 전달함수가 크게 감소하여 약 24 %의 오차가 확인되었다. 이는 선형 경계요소법 결과 기반으로 구축된 근사모델의 한계로 판단된다. 앞장에서 언급한바와 같은 얕은 수심에서 이동식 바닥판의 효과를 명확히 파악하기 위하여 비선형 파랑해석 또는 모형시험을 통한 면밀한 검토가 필요하다.
5. 결 론
본 연구에서는 심해공학수조의 기하학적 특성이 반영된 조파기 전달함수의 근사모델을 개발하였다. 심해공학수조의 기하학적 형상을 반영하기 위하여 2차원 주파수 영역 경계요소법을 사용하여 조파기의 경계치 문제를 해석하였다. 해석된 결과를 통하여 조류 유출구로 인한 계단지형과 이동식 바닥판으로 인한 기하학적 특성이 파랑 생성에 미치는 영향을 확인하였다. 해석된 경계요소법의 결과와 TPS model을 이용하여 조파기 전달함수의 근사모델을 개발하였다. 모형시험과 비교를 통하여 개발된 근사모델의 유효성을 확인하였다. 해당 연구를 통하여 아래와 같은 결론을 도출하였다.
(1) 심해공학수조의 경우, 조류 유출구로 인한 계단지형과 같은 수심변화가 발생하며 이는 파의 파장과 위상속도를 증가시킨다. 따라서 일반적인 수조와 비교하여 조파기 근처의 evanescent mode 및 위상의 변화가 발생한다.
(2) 조파기 전달함수 비교를 통해 이동식 바닥판이 수심 변화 효과를 잘 모사함을 확인하였다.
(3) 심해공학수조의 기하학적 특성으로 인하여 일반적인 수조의 조파기의 전달함수와 차이가 발생됨을 수치계산을 통하여 확인하였다. 해당 차이가 미소하기 때문에 3m 이상의 수심에서는 근사적으로 이론해의 사용이 가능하다고 판단된다. 하지만 3m 미만의 수심에서는 대체할 이론해가 없기 때문에 수치해석을 통한 조파기 전달함수의 확보는 물론 이를 효율적으로 활용하기 위한 근사모델이 필요하다.
(4) TPS model으로 정립한 근사모델과 경계요소법의 결과 값의 오차가 9.2815e-24로 근사모델의 정확성이 확인되었다.
(5) 모형시험 비교 결과, 개발된 근사모델이 1.0 m 이상 수심의 파 시험에서는 5%이하의 오차를 확인하여 근사모델의 타당성을 확인하였다. 하지만 0.5 m 수심에서는 약 24% 오차가 확인되었다. 이의 원인으로 선형해석의 결과를 기반한 모델의 한계로 파악된다.
추후 비선형 파랑시뮬레이션 또는 추가 모형시험을 통하여 해당 근사모델의 사용 가능 범위를 확인하고 근사모델을 보완하는 연구를 이어갈 예정이다.
Acknowledgements
본 연구는 선박해양프랜트연구소에서 지원하는 “심해용 복합해양 플랫폼 통합 성능평가 기술개발(PES4310)"의 결과물임을 밝히는 바입니다.