|
 |
| J Navig Port Res > Volume 46(3); 2022 > Article |
|
мҡ” м•Ҫ
ліё м—°кө¬лҠ” м •мғҒ к°ҖлҸҷ мӨ‘м—җлҸ„ нҡҢм „мҲҳк°Җ ліҖн•ҳлҠ” кё°кё°мқҳ мқҙмғҒ л°Ҹ кі мһҘ 진лӢЁ л°©м•Ҳмқ„ лӢӨлЈЁкі мһҲлӢӨ. нҡҢм „мҲҳк°Җ ліҖн•Ём—җ л”°лқј л№„м •мғҒм Ғ мӢңкі„м—ҙ нҠ№м„ұмқ„ лӮҙнҸ¬н•ң м„јм„ң лҚ°мқҙн„°м—җ кё°кі„н•ҷмҠөмқ„ м Ғмҡ©н• мҲҳ мһҲлҠ” м Ҳм°ЁлҘј м ңмӢңн•ҳкі мһҗ н•ҳмҳҖлӢӨ. кё°кі„н•ҷмҠөмңјлЎңлҠ” k-Nearest Neighbor(k-NN), Support Vector Machine(SVM), Random Forestмқ„ мӮ¬мҡ©н•ҳм—¬ мқҙмғҒ л°Ҹ кі мһҘ 진лӢЁмқ„ мҲҳн–үн•ҳмҳҖлӢӨ. лҳҗн•ң 진лӢЁ м •нҷ•м„ұмқ„ 비көҗн• лӘ©м ҒмңјлЎң мқҙмғҒ к°җм§Җм—җ мҳӨнҶ мқёмҪ”лҚ”, кі мһҘ진лӢЁм—җлҠ” н•©м„ұкіұ кё°л°ҳмқҳ Conv1DлҸ„ 추к°ҖлЎң мқҙмҡ©н•ҳмҳҖлӢӨ. л№„м •мғҒм Ғ мӢңкі„м—ҙлЎңл¶Җн„° нҶөкі„ л°Ҹ мЈјнҢҢмҲҳ мҶҚм„ұмңјлЎң кө¬м„ұлҗң мӢңкі„м—ҙ нҠ№м§• лІЎн„°лҘј 추м¶ңн•ҳкі , 추м¶ңлҗң нҠ№м§• лІЎн„°м—җ м •к·ңнҷ” л°Ҹ м°Ёмӣҗ 축мҶҢ кё°лІ•мқ„ м Ғмҡ©н•ҳмҳҖлӢӨ. нҠ№м§• лІЎн„°мқҳ м„ нғқкіј м •к·ңнҷ”, м°Ёмӣҗ 축мҶҢ м—¬л¶Җм—җ л”°лқј лӢ¬лқјм§ҖлҠ” кё°кі„н•ҷмҠөмқҳ 진лӢЁ м •нҷ•лҸ„лҘј 비көҗн•ҳмҳҖлӢӨ. лҳҗн•ң, м Ғмҡ©лҗң н•ҷмҠө м•Ңкі лҰ¬мҰҳ лі„лЎң мҙҲл§Өк°ңліҖмҲҳ мөңм Ғнҷ” кіјм •кіј м Ғмёө кө¬мЎ°лҘј м„ӨлӘ…н•ҳмҳҖлӢӨ. мөңмў…м ҒмңјлЎң кё°мЎҙмқҳ мӢ¬мёөн•ҷмҠөкіј 비көҗн•ҳм—¬, кё°кі„н•ҷмҠөлҸ„ к°ҖліҖ нҡҢм „кё°кё°мқҳ кі мһҘмқ„ м •нҷ•н•ҳкІҢ 진лӢЁн• мҲҳ мһҲлҠ” м Ҳм°ЁлҘј м ңмӢңн•ҳмҳҖлӢӨ.
ABSTRACT
This study examined the diagnostics of abnormalities and faults of equipment, whose rotational speed changes even during regular operation. The purpose of this study was to suggest a procedure that can properly apply machine learning to the time series data, comprising non-stationary characteristics as the rotational speed changes. Anomaly and fault diagnosis was performed using machine learning: k-Nearest Neighbor (k-NN), Support Vector Machine (SVM), and Random Forest. To compare the diagnostic accuracy, an autoencoder was used for anomaly detection and a convolution based Conv1D was additionally used for fault diagnosis. Feature vectors comprising statistical and frequency attributes were extracted, and normalization & dimensional reduction were applied to the extracted feature vectors. Changes in the diagnostic accuracy of machine learning according to feature selection, normalization, and dimensional reduction are explained. The hyperparameter optimization process and the layered structure are also described for each algorithm. Finally, results show that machine learning can accurately diagnose the failure of a variable-rotation machine under the appropriate feature treatment, although the convolution algorithms have been widely applied to the considered problem.
ліё м—°кө¬лҠ” мҡҙм „ мЎ°кұҙм—җ л”°лқј нҡҢм „ мҶҚлҸ„к°Җ ліҖн•ҳлҠ” к°ҖліҖ нҡҢм „кё°кё°мқҳ мқҙмғҒк°җм§Җ л°Ҹ кі мһҘ진лӢЁмқ„ мң„н•ң нҡЁкіјм Ғмқё м•Ңкі лҰ¬мҰҳ м„ нғқм—җ кҙҖмӢ¬мқ„ л‘җкі мһҲлӢӨ. н„°л№Ҳ, нҺҢн”„, 압축기, кё°м–ҙмһҘм№ҳ л“ұмқҳ нҡҢм „кё°кё°лҠ” м§Ҳлҹү л¶Ҳк· нҳ•, 축 м •л ¬ л¶Ҳлҹү, лІ м–ҙл§Ғ кІ°н•Ё, кё°кі„м Ғ лҠҗмҠЁн•Ё л“ұкіј к°ҷмқҖ кі мһҘмқҳ к°ҖлҠҘм„ұмқ„ к°Җм§Җкі мһҲмңјл©° мөңк·ј нҡҢм „кё°кё°мқҳ кі мҶҚнҷ”, ліөмһЎнҷ”, м •л°Җнҷ” кІҪн–ҘмңјлЎң мқён•ҙ кі мһҘ진лӢЁкіј мҳҲл°©мқҖ м—¬м „нһҲ мӨ‘мҡ”н•ң л¬ём ңмқҙлӢӨ. нҡҢм „ кё°кё°мқҳ 진лҸҷмӢ нҳёк°Җ м •мғҒм Ғ(Stationary)мқј кІҪмҡ°, мӢңкі„м—ҙ нҠ№м§•(Feature)мқ„ кё°кі„н•ҷмҠө 분лҘҳ л°Ҹ мҳҲмёЎ м•Ңкі лҰ¬мҰҳмқҳ н•ҷмҠөм—җ мӮ¬мҡ©н•ЁмңјлЎңмҚЁ нҡЁмңЁм ҒмңјлЎң кі мһҘмқ„ 분лҘҳн• мҲҳ мһҲлӢӨ. мҰү, мӢңкі„м—ҙмқҳ нҶөкі„м Ғ мҶҚм„ұмқё RMS(Root mean square), Peak-peak, Skewness, Crest factor, Kurtosis л“ұмқҳ к°’мқ„ нҠ№м§• лІЎн„°лЎң м Ғмҡ©н• мҲҳ мһҲлӢӨ(Riaz et al., 2017). мӢ нҳёмқҳ RMS, Kurtosis, Crest Factor л“ұ нҶөкі„м Ғ нҠ№м§•мқ„ кё°кі„н•ҷмҠөм—җ мӮ¬мҡ©н•ҳм—¬ кі мһҘмқ„ 분лҘҳн•ң мӮ¬лЎҖлҠ” лӢӨмҲҳ м°ҫмқ„ мҲҳ мһҲлӢӨ(Sreejith et al., 2008; Li et al., 2015). мң„мҷҖ к°ҷмқҙ нҠ№м§• лІЎн„°лҘј мқҙмҡ©н•ң м•Ңкі лҰ¬мҰҳмқҖ мқјм •н•ң нҡҢм „ мЎ°кұҙмқҳ мӢңмҠӨн…ңм—җм„ң л°ңмғқн•ҳлҠ” кі мһҘ мӢ нҳёлҘј к°җм§Җн•ҳлҠ” лҚ° м Ғн•©н•ҳлӢӨ. мқҙм—җ л°ҳн•ҳм—¬, н’Қл Ҙ н„°л№Ҳмқҳ мң м„ұ кё°м–ҙл°•мҠӨ к°ҷмқҙ к°ҖліҖ нҡҢм „ кё°кё°мқҳ мғҒнғң мӢ нҳёлҠ” л№„м •мғҒ(Non-stationary) нҠ№м§•мқ„ ліҙмқҙкё° л•Ңл¬ём—җ нҶөкі„ лҳҗлҠ” мЈјнҢҢмҲҳ нҠ№м„ұ л§ҢмңјлЎңлҠ” м •нҷ•н•ң кі мһҘ진лӢЁмқҙ м–ҙл өлӢӨкі м•Ңл Өм ё мһҲлӢӨ(Bartelmus et al., 2010; Feng and Liang, 2014; Kan et al., 2015). к·ёлҹ¬лӮҳ, Pestana-Viana et al. (2016) мқҖ ліҖмҶҚ мЎ°кұҙмқ„ к°Җ진 진лҸҷ мӢ нҳёлЎңл¶Җн„° м—”нҠёлЎңн”ј(Entropy), к·ёлҰ¬кі мІЁлҸ„(Kurtosis) л“ұмңјлЎң нҠ№м§• лІЎн„°лҘј кө¬м„ұн•ҳкі , ANNмқ„ мқҙмҡ©н•ҳм—¬ м§Ҳлҹү л¶Ҳк· нҳ•кіј 축 м •л ¬ л¶Ҳлҹүмқҳ кі мһҘмқ„ 분лҘҳн•ҳмҳҖмңјлӮҳ, м •нҷ•лҸ„к°Җ лҶ’м§Җ м•ҠмқҖ лӢЁм җмқ„ к°Җм§Җкі мһҲлӢӨ. н•ңнҺё, мӢ¬мёөн•ҷмҠөмқ„ нҷңмҡ©н•ң кі мһҘ진лӢЁ л°©лІ•мқҖ н•©м„ұкіұмңјлЎң мӢ нҳёмқҳ кі мң н•ң нҠ№м„ұмқ„ м—°мӮ°н•ҳкё° л•Ңл¬ём—җ нҠ№м§• м„ нғқмқҳ мқҳмЎҙлҸ„к°Җ м—ҶлҠ” мһҘм җмқҙ мһҲлӢӨ(Liao et al., 2020). нҠ№нһҲ, мӢңк°„-мЈјнҢҢмҲҳ ліҖнҷҳ(мҳҲ: Wavelet ліҖнҷҳ, Hilbert huang ліҖнҷҳ, Short time fourier ліҖнҷҳ)мңјлЎң м–»мқҖ мЈјнҢҢмҲҳ мқҙлҜём§Җм—җ мӢ¬мёөн•ҷмҠөмқ„ м Ғмҡ©н•ҳм—¬ кі мһҘмқ„ нҢҗлі„н•ҳл©ҙ лҶ’мқҖ 진лӢЁ м •нҷ•лҸ„лҘј м–»лҠ” лӢӨлҠ” кІғмқҙ л„җлҰ¬ м•Ңл Өм ё мһҲлӢӨ(Verstraete et al., 2017; Yuan et al., 2018; Tao et al., 2020). л”°лқјм„ң мҶҚлҸ„ ліҖлҸҷмқҙ мһҲлҠ” мӢңкі„м—ҙм—җ н•©м„ұкіұмқ„ м§Ғм ‘ м Ғмҡ©н•ҳлҠ” CNN (Convolutional neural network) кі„м—ҙмқҳ мӢ¬мёөн•ҷмҠөмқҙ нҡЁмңЁм Ғмқё кІғмңјлЎң м•Ңл Өм ё мһҲлӢӨ(Qiao et al., 2020). к·ёлҹ¬лӮҳ, CNNмқҖ н’Җл§Ғ(Pooling) кіјм •м—җм„ң м •ліҙк°Җ мҶҗмӢӨлҗҳкұ°лӮҳ, н•©м„ұкіұ кі„мӮ°м—җ л§ҺмқҖ м—°мӮ° мӢңк°„мқҙ н•„мҡ”н•ҳлӢӨлҠ” м җ л•Ңл¬ём—җ мӢӨмӢңк°„ 진лӢЁ мёЎл©ҙм—җм„ңлҠ” лӢЁм җмқ„ к°Җм§Җкі мһҲлӢӨ.
мң„мҷҖ к°ҷмқҖ л°°кІҪм—җм„ң ліё м—°кө¬лҠ” ліҖлҸҷ мҶҚлҸ„лҘј к°Җ진 нҡҢм „кё°кё°мқҳ кі мһҘ진лӢЁм—җм„ң мӢ¬мёөн•ҷмҠө мҲҳмӨҖмқҳ м •нҷ•м„ұмқ„ к°Җ진 кё°кі„н•ҷмҠөмқҳ м Ғмҡ© м Ҳм°ЁлҘј м ңмӢңн•ҳкі мһҗ н•ңлӢӨ. нҠ№нһҲ, кё°кі„н•ҷмҠө м Ғмҡ© кіјм •м—җм„ң мһҘ비мқҳ л№„м •мғҒм„ұмқ„ л°ҳмҳҒн• мҲҳ мһҲлҠ” л°©м•Ҳмқ„ м ңм•Ҳн•ҳкі мӢ¬мёөн•ҷмҠөмқҳ м •нҷ•м„ұкіј 비көҗн•ҳкі мһҗ н•ңлӢӨ. мқҙлҘј нҶөн•ҳм—¬ ліҖмҶҚмЎ°кұҙмқҳ кі мһҘ 진лӢЁм—җ мһҲм–ҙм„ң кё°кі„н•ҷмҠөмқҳ м Ғмҡ© к°ҖлҠҘм„ұмқ„ нҷ•мқён•ҳкі мһҗ н•ңлӢӨ.
ліё мһҘм—җм„ңлҠ” 진лӢЁм—җ м Ғмҡ©н•ң м•Ңкі лҰ¬мҰҳмқ„ м„ӨлӘ…н•ҳмҳҖлӢӨ. Table 1 м—җ м Ҳм°Ё лі„лЎң м•Ңкі лҰ¬мҰҳмқ„ м •лҰ¬н•ҳмҳҖлӢӨ. мқҙмғҒк°җм§ҖлҠ” мһҘ비мқҳ м •мғҒ к°ҖлҸҷ мң л¬ҙлҘј кө¬лі„н•ҳлҠ” м Ҳм°ЁлҘј мқҳлҜён•ҳл©°, кё°кі„н•ҷмҠө 분лҘҳ кё°лІ•мқё k-NN кіј SVM, к·ёлҰ¬кі Random forest лҘј м Ғмҡ©н•ҳмҳҖлӢӨ. лҳҗн•ң кі мһҘ мӢ нҳёк°Җ м—ҶлҠ” кІҪмҡ°м—җлҸ„ мқҙмғҒ к°җм§Җк°Җ к°ҖлҠҘн•ҳлҸ„лЎқ мҳӨнҶ мқёмҪ”лҚ”лҸ„ м Ғмҡ©н•ҳмҳҖлӢӨ. н•ңнҺё, кі мһҘ진лӢЁм—җлҠ” кё°кі„н•ҷмҠөкіј мӢ¬мёөн•ҷмҠөмқ„ м Ғмҡ©н•ҳмҳҖлӢӨ. лҳҗн•ң, кі мһҘ 진лӢЁмқҳ м •нҷ•лҸ„лҘј 비көҗн• лӘ©м ҒмңјлЎң CNN лӘЁлҚёмқё Conv1D лҸ„ м Ғмҡ©н•ҳм—¬ кі мһҘмқ„ 분лҘҳн•ҳмҳҖлӢӨ.
k-NN мқҖ лҚ°мқҙн„° 집합 лӮҙм—җ мң мӮ¬н•ң мҶҚм„ұмқ„ к°Җ진 мқёмҠӨн„ҙмҠӨ лӘЁмһ„мқҙ к·јм ‘н•ҳм—¬ мЎҙмһ¬н•ңлӢӨлҠ” к°Җм •м—җ кё°л°ҳн•ң м•Ңкі лҰ¬мҰҳмқҙлӢӨ(Cover and Hart, 1967). SVM мқҖ нҠ№м§• лІЎн„°мқҳ кіөк°„м—җм„ң лҚ°мқҙн„° к°„мқҳ кІҪкі„лҘј м„Өм •н•ҳлҠ” м•Ңкі лҰ¬мҰҳмқҙл©°, кІҪкі„лҘј лҢҖн‘ңн•ҳлҠ” м»Өл„җ н•ЁмҲҳлҘј кІ°м •н•ҙм•јн•ңлӢӨ (Xing et al., 2017; Wang et el., 2021). Random forest лҠ” мқҳмӮ¬ кІ°м • л°©лІ•мңјлЎң нҡҢк·Җ 분м„қ л°Ҹ 분лҘҳлҘј мҲҳн–үн•ҳлҠ” л°©лІ•мқҙлӢӨ(Breiman, 2001). мҳӨнҶ мқёмҪ”лҚ”лҠ” м •мғҒ лҚ°мқҙн„°лҘј 축мҶҢлҗң м°ЁмӣҗмңјлЎң 압축 нӣ„м—җ лӢӨмӢң ліөмӣҗн•ҳкі , ліөмӣҗлҗң лҚ°мқҙн„°мҷҖ мӣҗліёмқҳ м°ЁмқҙлЎңл¶Җн„° мқҙмғҒ мң л¬ҙлҘј нҢҗлӢЁн•ҳлҠ” л°©лІ•мқҙлӢӨ. мқҙлҠ” кі мһҘ л Ҳмқҙлё”(Label)мқҙ мЎҙмһ¬н•ҳм§Җ м•ҠлҠ” м •мғҒ мӢ нҳёл§ҢмңјлЎң л№„м •мғҒмқ„ нҢҗлі„н•ҳлҠ” кё°лІ•мқҙлӢӨ(Lee, 2021). н•ңнҺё, Conv1D лҠ” 1 м°Ёмӣҗ м»Өл„җ н•„н„°к°Җ мһ…л Ҙ к°’мқ„ мқҙлҸҷн•ҳл©° н•©м„ұкіұ м—°мӮ°мқ„ мҲҳн–үн•ҳм—¬ ліҖнҷҳлҗң л°°м—ҙмқ„ кі„мӮ°н•ңлӢӨ. мқём ‘н•ң л°°м—ҙ мёөмқҳ м»Өл„җ нҒ¬кё°м—җ н•ҙлӢ№н•ҳлҠ” л…ёл“ңмҷҖ м„ нҳ• кІ°н•©мқ„ нҶөн•ҙ мқҙл“Ө мӮ¬мқҙм—җ нҢЁн„ҙмқ„ мқёмӢқн•ҳлҠ” л°©лІ•мқҙлӢӨ(Wang, 2019; Faust et al., 2018). лӘЁл“ м•Ңкі лҰ¬мҰҳмқҖ нҢҢмқҙмҚ¬ кё°л°ҳмңјлЎң кө¬нҳ„н•ҳкі , кё°кі„н•ҷмҠөм—җлҠ” Scikit-learn, мҳӨнҶ мқёмҪ”лҚ”мҷҖ Conv1D лҠ” Keras лӘЁл“Ҳмқ„ к°Ғк°Ғ мӮ¬мҡ©н•ҳмҳҖлӢӨ. лҚ°мқҙн„° м „мІҳлҰ¬ кіјм •м—җлҠ” Numpy л°Ҹ Matplotlib лӘЁл“Ҳмқ„ мӮ¬мҡ©н•ҳмҳҖлӢӨ.
кё°кі„н•ҷмҠөмқҖ лҚ°мқҙн„° м „мІҳлҰ¬, нҠ№м§• 추м¶ң, н•ҷмҠө л°Ҹ мөңм Ғнҷ” кіјм •мқ„ кұ°міӨлӢӨ. к°Ғ кё°кі„н•ҷмҠө м•Ңкі лҰ¬мҰҳмқҳ мҙҲл§Өк°ңліҖмҲҳ мөңм Ғнҷ” кіјм •мқҖ 4 мһҘм—җ мғҒм„ён•ҳкІҢ кё°мҲ н•ҳмҳҖлӢӨ. мҳӨнҶ мқёмҪ”лҚ” кё°л°ҳмқҳ мқҙмғҒк°җм§Җ лӘЁлҚёлҸ„ Fig. 1 кіј к°ҷмқҙ лҚ°мқҙн„° м „мІҳлҰ¬, нҠ№м§• 추м¶ң, н•ҷмҠө м Ҳм°ЁлЎң м Ғмҡ©н•ҳмҳҖлӢӨ. мқёмҪ”лҚ” мёөкіј л””мҪ”лҚ”мёөмқ„ 2 к°ңм”© мҢ“мқҖ м Ғмёөмқ„ кө¬м„ұн•ҳкі , кё°кі„н•ҷмҠөм—җм„ң мӮ¬мҡ©н•ҳмҳҖлҚҳ нҠ№м§• лІЎн„°лҘј мҳӨнҶ мқёмҪ”лҚ”мқҳ н•ҷмҠө кіјм •м—җлҸ„ мӮ¬мҡ©н•ҳм—¬ м—°мӮ° мӢңк°„мқ„ лӢЁм¶•мӢңмј°лӢӨ. к·ё нӣ„м—җ м •мғҒ мғҳн”Ңм—җм„ң 추м¶ңн•ң нҠ№м§• лІЎн„°лЎңмҚЁ мҳӨнҶ мқёмҪ”лҚ”лҘј н•ҷмҠөмӢңнӮЁ нӣ„м—җ, мһ…л Ҙлҗң мӢ нҳёмқҳ ліөмӣҗ мҳӨлҘҳлҘј м •мғҒ мғҳн”Ңмқҳ к°’кіј 비көҗн•ҳм—¬ л№„м •мғҒ м—¬л¶ҖлҘј нҢҗлӢЁн•ҳмҳҖлӢӨ. мқҙл•Ң MAE(Mean absolute error)лҘј ліөмӣҗмҳӨлҘҳ л°Ҹ м •мғҒ нҢҗлӢЁмқҳ кё°мӨҖмңјлЎң м„ нғқн•ҳмҳҖлӢӨ.
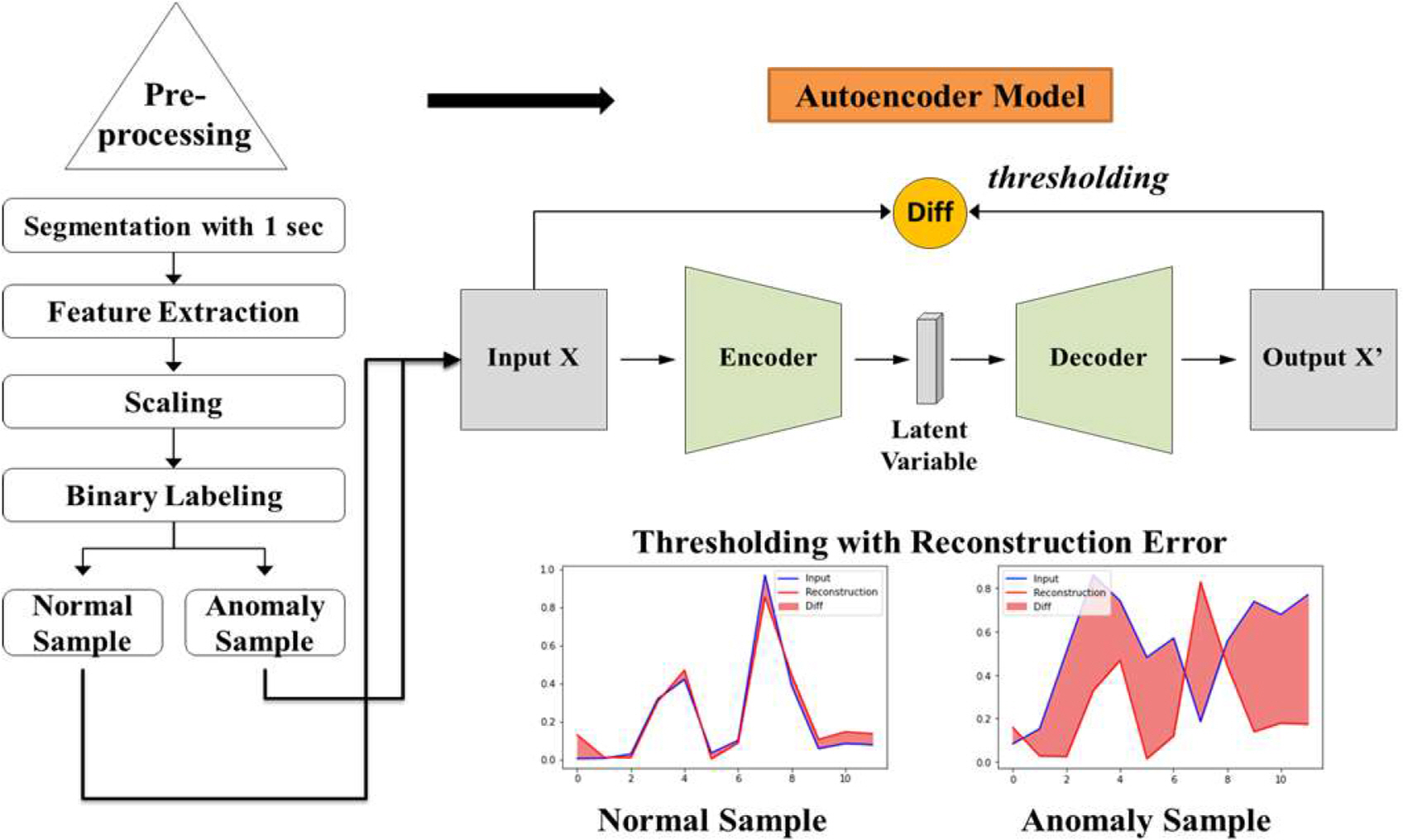
кі мһҘ 진лӢЁм—җ м Ғмҡ©н•ң Conv1D мқҳ м Ғмёө кө¬мЎ°лҠ” Fig. 2 м—җ мҡ”м•Ҫн•ҳмҳҖлӢӨ. л‘җ к°ңмқҳ н•©м„ұ мёө(Convolutional layer)кіј н’Җл§Ғмёө(Pooling layer)мңјлЎң мӢ кІҪл§қмқ„ кө¬м„ұн•ҳмҳҖлӢӨ. н•ҷмҠөм—җ мӮ¬мҡ©н• мӣҗлһҳ 진лҸҷ мӢ нҳёлҠ” лӢӨмҡҙ мғҳн”Ңл§Ғн•ҳм—¬ кі„мӮ°мӢңк°„мқ„ лӢЁм¶•н•ҳмҳҖлӢӨ. лҳҗн•ң м Җм—ӯ нҶөкіј н•„н„°лҘј 추к°ҖлЎң м Ғмҡ©н•ҳм—¬ мӢ нҳёмқҳ мҷңкіЎ нҳ„мғҒмқё м—җмқјлҰ¬м–ҙмӢұ(Aliasing)мқ„ л°©м§Җн•ҳмҳҖлӢӨ. лӢӨмқҢмңјлЎң н•©м„ұмёөмқҙ м „мІҳлҰ¬лҘј кұ°м№ң 진лҸҷмӢ нҳёлҘј м—°мӮ°н•ҳм—¬ нҠ№м§•мқ„ 추м¶ңн•ҳлҸ„лЎқ н•ҳкі , н’Җл§Ғ мёөмқҖ н•©м„ұмёөмқҙ м—°мӮ°н•ң нҠ№м§• лІЎн„°лҘј 압축н•ҳм—¬ кі„мӮ° мӢңк°„мқҙ лӢЁм¶•лҗҳлҸ„лЎқ н•ҳмҳҖлӢӨ. л§Ҳм§Җл§үмңјлЎң 추м¶ңн•ң нҠ№м§•мқ„ мҷ„м „ м—°кІ°мёөкіј м—°кІ°н•ЁмңјлЎңмҚЁ кі мһҘ лӘЁл“ңлЎң 분лҘҳн•ҳлҠ” м¶ңл Ҙ мёөмқ„ м§Җм •н•ҳмҳҖлӢӨ.
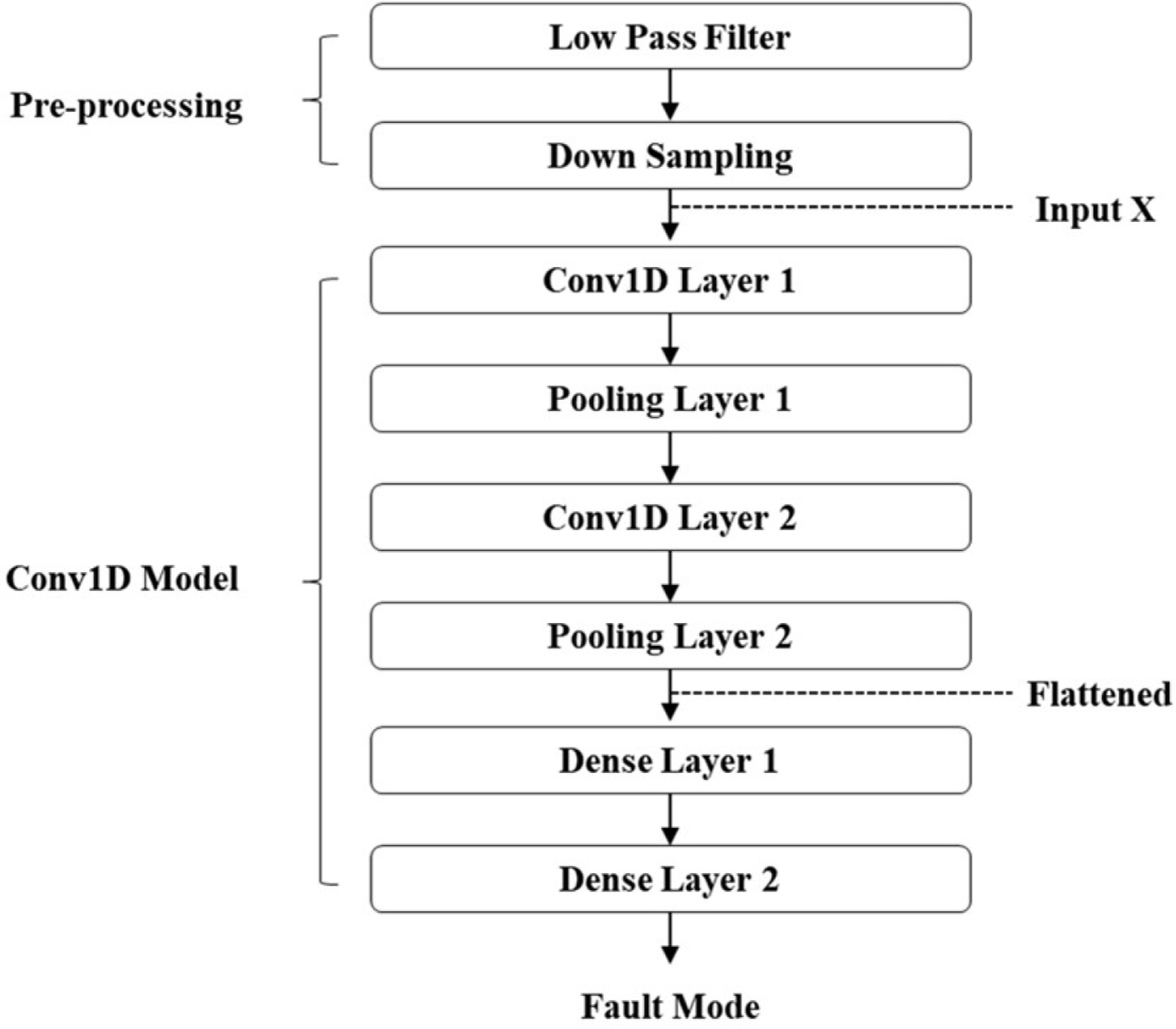
кі мһҘ н•ҷмҠөм—җлҠ” Fig. 3 м—җ ліҙмқё кІ°н•Ё лӘЁмқҳмӢӨн—ҳмһҘ비м—җм„ң кі„мёЎн•ң MAFAULDA (Machinery fault database) лҚ°мқҙн„°лҘј мӮ¬мҡ©н•ҳмҳҖлӢӨ(de Lima et al., 2013). MAFAULDA лҠ” к°ҖліҖ нҡҢм „кё°кё°мқҳ кі мһҘ 진лӢЁм—җм„ң м•Ңкі лҰ¬мҰҳ 비көҗ кІҖмҰқ л°Ҹ м •нҷ•м„ұ лІӨм№ҳл§ҲнҒ¬м—җ л„җлҰ¬ мӮ¬мҡ©лҗҳкі мһҲлӢӨ (Ali et al., 2019). лӘЁмқҳмӢӨн—ҳмһҘ비лҠ” лӘЁн„°, 축, лІ м–ҙл§Ғ л“ұмңјлЎң кө¬м„ұлҗҳм–ҙ мһҲмңјл©°, 2 к°ңмқҳ лІ м–ҙл§Ғм—җ к°ҖмҶҚлҸ„ м„јм„ңлҘј к°Ғк°Ғ л¶Җм°©н•ҳм—¬ 3 л°©н–Ҙмқҳ к°ҖмҶҚлҸ„лҘј кі„мёЎн•ҳмҳҖлӢӨ. 축 м •л ¬ л¶Ҳлҹү, м§Ҳлҹү л¶Ҳк· нҳ• л°Ҹ лІ м–ҙл§Ғ кІ°н•Ёмқ„ мқёмң„м ҒмңјлЎң л°ңмғқмӢңнӮӨкі , ліҖмҶҚмЎ°кұҙм—җм„ң мӢ нҳёк°Җ кі„мёЎлҗҳм—ҲлӢӨ. мҙқ 8 к°ңмқҳ мӢ нҳёлЎң кө¬м„ұлҗҳм–ҙ мһҲмңјл©°, нҡҢм „ мҶҚлҸ„кі„, 6 к°ңмқҳ к°ҖмҶҚлҸ„кі„, мқҢн–Ҙ м„јм„ңлЎңл¶Җн„° мҙҲлӢ№ 50kHz лЎң мӢ нҳёк°Җ кё°лЎқлҗҳм—ҲлӢӨ. н•ҷмҠөм—җ мӮ¬мҡ©н•ң мӢ нҳёлҠ” 880 к°ңмқҳ нҢҢмқјлЎң кө¬м„ұлҗҳм–ҙ мһҲмңјл©°, к°Ғ нҢҢмқјмқҖ 5 мҙҲм”© кё°лЎқлҗҳм—ҲлӢӨ. н•ҷмҠө лҚ°мқҙн„°лҠ” лӢӨмқҢкіј к°ҷмқҙ кө¬м„ұлҗҳм–ҙ мһҲлӢӨ.
вҖў м •мғҒ: 49 к°ң лҚ°мқҙн„°лЎң кө¬м„ұлҗЁ (н–үл ¬= 12,250,000Г—8)
вҖў м§Ҳлҹү л¶Ҳк· нҳ•: л¶Ҳк· нҳ• м§Ҳлҹү(6~35 g) 축м—җ л¶Җк°Җлҗң 333 к°ң лҚ°мқҙн„° (н–үл ¬= 83,250,000Г—8)
вҖў мҲҳнҸү축 м •л ¬ л¶Ҳлҹү: 0.5~2.0mm мқҳ мҲҳнҸү 축 нҺёмӢ¬мқҙ л¶Җк°Җлҗң 197 к°ңмқҳ мғҳн”Ң(н–үл ¬= 49,250,000Г—8)
вҖў мҲҳм§Ғ축 м •л ¬ л¶Ҳлҹү: мҲҳм§Ғ 축 нҺёмӢ¬ (0.51~1.90mm)мқҙ л§Ңл“Өм–ҙ진, 301 к°ңмқҳ мғҳн”Ң(н–үл ¬=75,250,000Г—8)
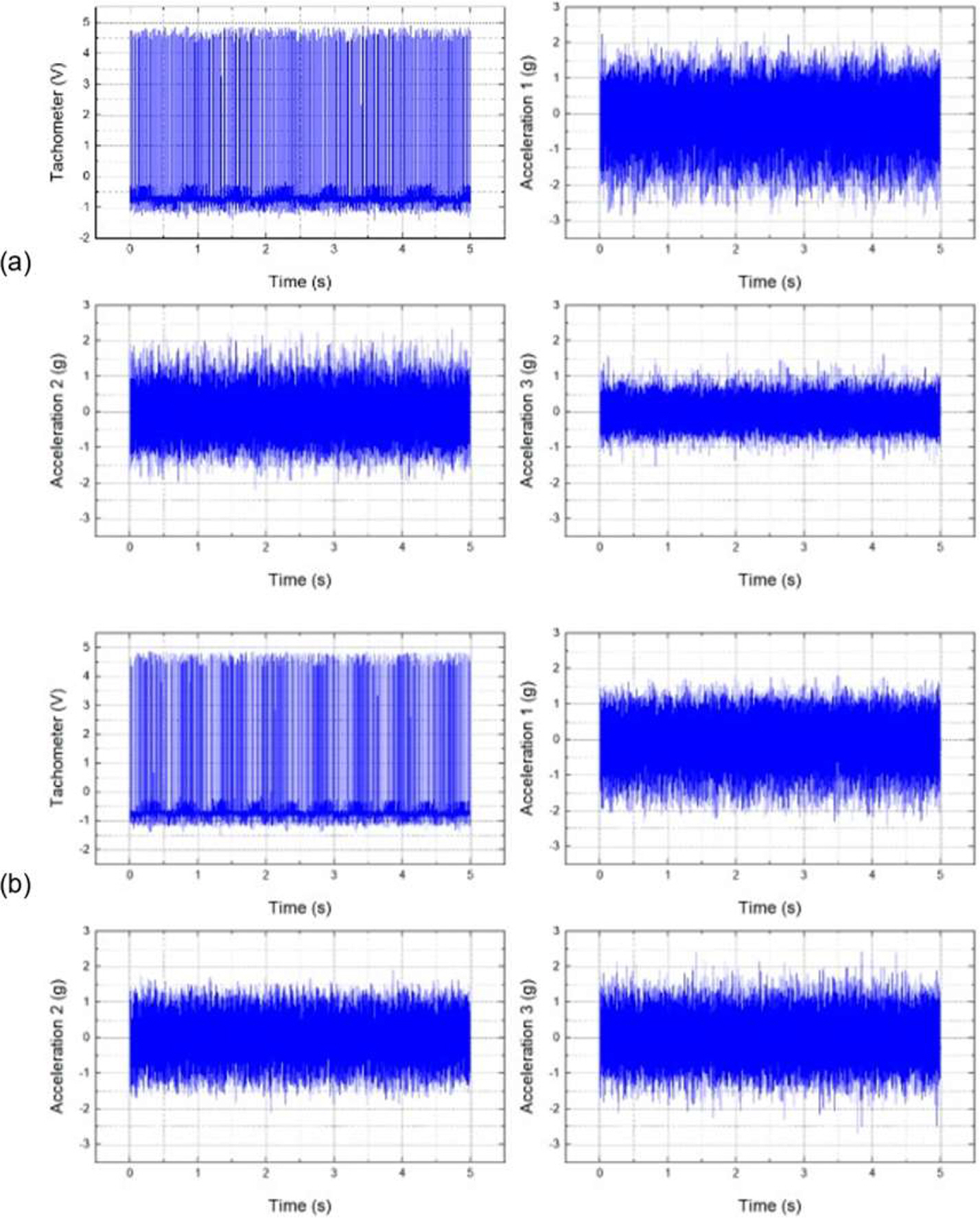
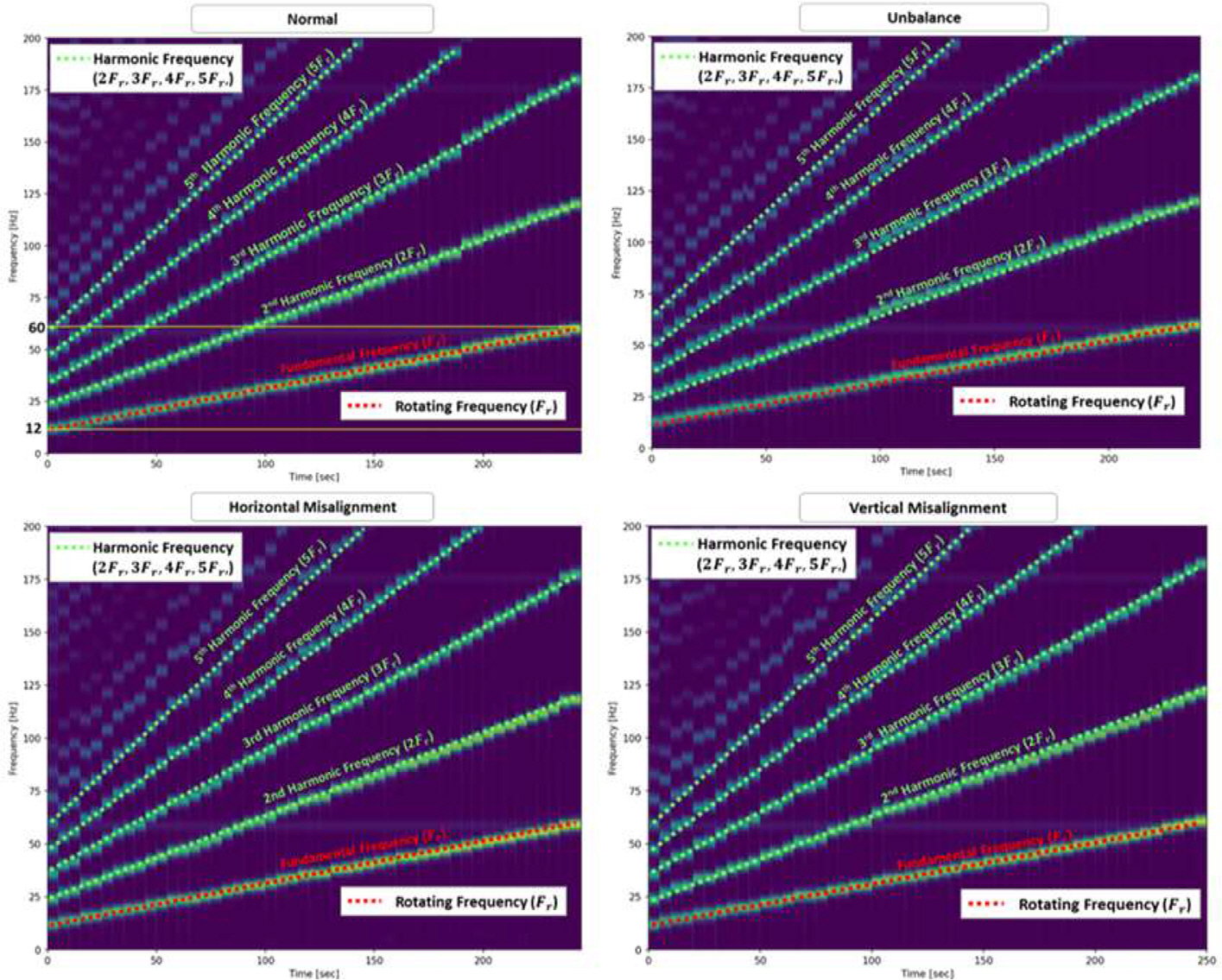
м •мғҒ мғҒнғңмҷҖ 축 м •л ¬л¶Ҳлҹү мғҒнғңмқҳ мқјл¶ҖлҘј Fig. 4 м—җ ліҙмҳҖлӢӨ. кі мһҘ мў…лҘҳм—җ л”°лқј 진нҸӯ м°Ёмқҙк°Җ мЎҙмһ¬н–ҲмңјлӮҳ мңЎм•ҲмңјлЎң кі мһҘмқ„ мӢқлі„н•ҳкё°лҠ” м–ҙл Өмӣ лӢӨ. нҡҢм „мҲҳ ліҖнҷ”лҘј нҢҢм•…н•ҳкё° мң„н•ҳм—¬ к°ҖмҶҚлҸ„ мӢ нҳёлҘј STFT лЎң 분м„қн•ҳмҳҖмңјл©°, Fig. 5 м—җ кІ°кіјлҘј м ңмӢңн•ҳмҳҖлӢӨ. нҡҢм „ мЈјнҢҢмҲҳлҠ” м•Ҫ 12 Hz м—җм„ң 60Hz к№Ңм§Җ м„ нҳ•м ҒмңјлЎң мҰқк°Җн•ҳмҳҖмңјл©°, нҡҢм „мҶҚлҸ„ ліҖнҷ”лҠ” 12 RPM/s лЎң кі„мӮ°лҗҳм—ҲлӢӨ.
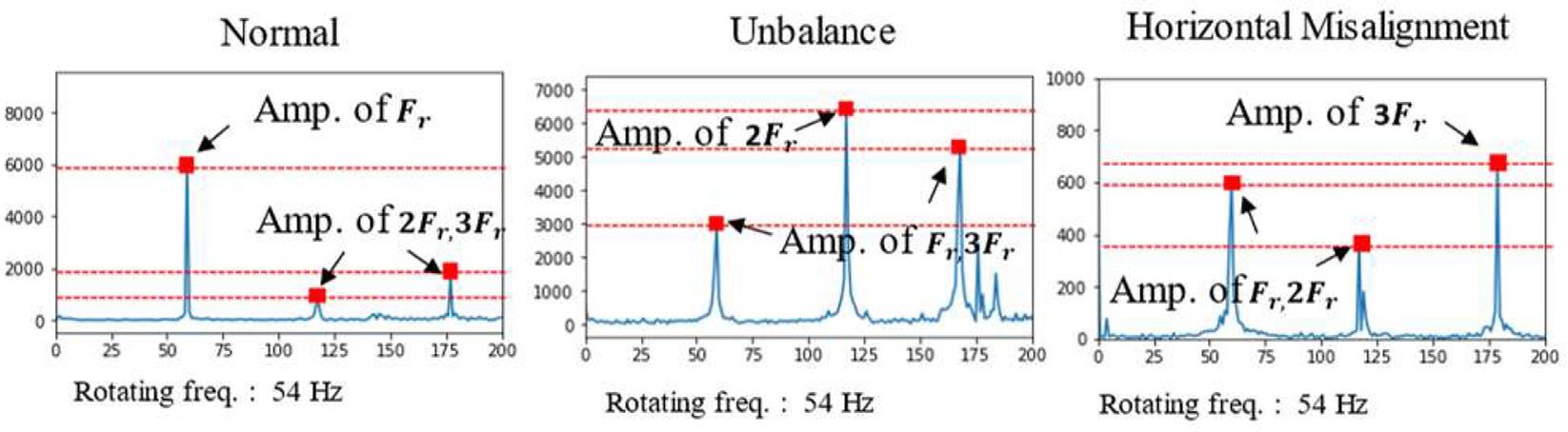
лЁјм Җ, н•ҷмҠө лҚ°мқҙн„° мӨ‘ м •мғҒ мғҳн”Ңкіј кі мһҘ мғҳн”Ңмқ„ к°Ғк°Ғ вҖҳNormalвҖҷ, вҖҳAnomalyвҖҷ л Ҳмқҙлё”мқ„ л¶Җм—¬н•ҳмҳҖмңјл©°, кі мһҘ мң нҳ• лі„лЎң л Ҳмқҙлё”мқ„ 추к°ҖлЎң л¶Җм—¬н•ҳмҳҖлӢӨ. мӣҗ мӢ нҳёлҠ” 1мҙҲлЎң л¶„н• н•ҳкі , к°Ғ мӢңл¶„н• к°„кІ©м—җм„ң кі„мӮ°н•ң нҶөкі„ к°’мқ„ мӢңкі„м—ҙ лІЎн„°лЎң кө¬м„ұн•ҳмҳҖлӢӨ. нҶөкі„ к°’мңјлЎңлҠ” м ҲлҢ“к°’ нҸүк· (xabs), мӢӨнҡЁм№ҳ(xrms), мҷңлҸ„(xskew), мІЁлҸ„(xkurt)лҘј м„ нғқн•ҳм—¬ нҠ№м§• лІЎн„°лҘј кө¬м„ұн•ҳмҳҖлӢӨ. Pestana-Viana et al.(2016)лҠ” MAFULDA лҚ°мқҙн„°лЎңл¶Җн„° нҶөкі„м Ғ мҶҚм„ұ л§Ңмқ„ нҠ№м§• лІЎн„°лЎң м„ нғқн•ҳм—¬ мӢ кІҪл§қ м•Ңкі лҰ¬мҰҳм—җ м Ғмҡ©н•ҳм—¬ кі мһҘмқ„ 진лӢЁн•ҳл©ҙ м•Ҫ 81.2%мқҳ м •нҷ•лҸ„лҘј ліҙмһ„мқ„ м ңмӢңн•ҳмҳҖлӢӨ. мқҙлҠ” нҡҢм „мҲҳ(мЈјнҢҢмҲҳ) ліҖнҷ”мқҳ мҶҚм„ұмқҙ нҸ¬н•Ёлҗҳм§Җ м•ҠмқҖ кІғмңјлЎң нҢҗлӢЁлҗңлӢӨ. л”°лқјм„ң ліё м—°кө¬м—җм„ңлҠ” кі мһҘ мң нҳ•м—җ л”°лқј мЈјнҢҢмҲҳ к°„мқҳ мғҒлҢҖм Ғмқё 진нҸӯм°Ёмқҙк°Җ мһҲлҠ” кІғмқ„ кі л Өн•ҳм—¬, кі мң мЈјнҢҢмҲҳ(Fr)мҷҖ мЎ°нҷ” мЈјнҢҢмҲҳ(2Fr,3Fr)мқҳ 진нҸӯмқ„ мЈјнҢҢмҲҳ нҠ№м„ұ к°’мңјлЎң 추к°ҖлЎң м Ғмҡ©н•ҳмҳҖлӢӨ. Fig. 6мқҖ мЎ°нҷ” мЈјнҢҢмҲҳ лі„лЎң 진нҸӯмқ„ ліҙмқё кІғмқҙлӢӨ. л”°лқјм„ң, Table 2м—җ ліҙмқё кІғкіј к°ҷмқҙ к°Ғ 진лҸҷ мӢ нҳё лі„лЎң 7к°ңмқҳ нҶөкі„ мҶҚм„ұкіј мЎ°нҷ” мЈјнҢҢмҲҳ мҶҚм„ұ к°’мңјлЎң нҠ№м§• лІЎн„°лҘј кө¬м„ұн•ҳмҳҖкі , 6к°ңмқҳ 진лҸҷ лҚ°мқҙн„°лҘј л°ҳмҳҒн•ҳм—¬ лӘЁл‘җ 42к°ңмқҳ нҠ№м§• лІЎн„°(fraw)мқ„ 추м¶ңн•ҳмҳҖлӢӨ.
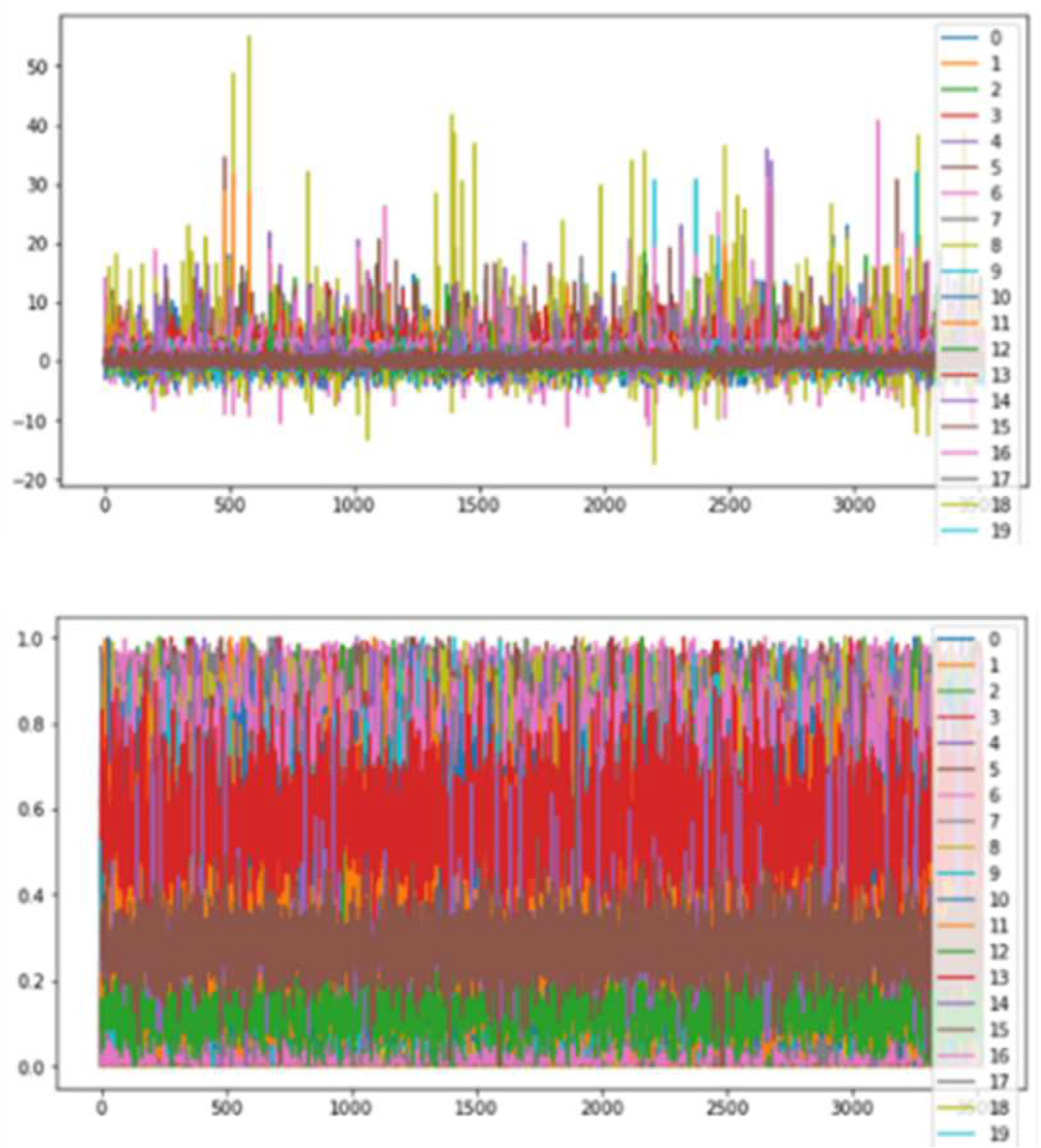
м•һм Ҳм—җм„ң кө¬н•ң нҠ№м§• лІЎн„°(fraw)лҠ” кіјм Ғн•©мқ„ мқјмңјнӮ¬ мҲҳ мһҲмңјлҜҖлЎң, м№ҙмқҙ м ңкіұ(Chi-square, ПҮ2) нҠ№м§•м„ нғқ л°Ҹ мЈјм„ұ분 분м„қмқ„ м Ғмҡ©н•ҳм—¬ к°Ғк°Ғ мғҒмң„ мғҒкҙҖлҸ„лҘј к°Җ진 10к°ңмқҳ м№ҙмқҙ м ңкіұ кё°л°ҳ нҠ№м§• лІЎн„°(fChi)мҷҖ м°Ёмӣҗ 축мҶҢлҗң нҠ№м§• лІЎн„°(fPCA)лҘј н•ҷмҠө лҚ°мқҙн„°лЎң мқҙмҡ©н•ҳмҳҖлӢӨ. к°Ғ нҠ№м§•лІЎн„°м—җ Robust л°Ҹ MinmaxмҠӨмјҖмқјл§Ғмқ„ м Ғмҡ©н•ҳмҳҖмңјл©°, Fig. 7м—җ к·ё кІ°кіјлҘј м ңмӢңн•ҳмҳҖлӢӨ.
k-л¶„н• көҗм°Ё кІҖмҰқ(k-Fold cross validation)кіј кІ©мһҗ нғҗмғү(Grid search)мқ„ мӮ¬мҡ©н•ҳм—¬ мҙҲл§Өк°ңліҖмҲҳлҘј мөңм Ғнҷ”н•ҳмҳҖлӢӨ (Bui et al., 2012; Refaeilzadeh et al., 2009). мқҙ кіјм •м—җм„ң k-NNмқҳ л§Өк°ң ліҖмҲҳлЎң n_neighborsлҠ” [1~9], weightsлҠ” [uniform, distance]лҘј мӮ¬мҡ©н•ҳкі , к°ҖмӨ‘м№ҳ кІ°м • м•Ңкі лҰ¬мҰҳмқҖ ball_treeмҷҖ kd_tree л°Ҹ bruteлҘј мӮ¬мҡ©н•ҳмҳҖлӢӨ. GridSearchмқҳ cv = 3, refit = True, return_train_score = True лЎң м„Өм •н•ҳмҳҖлӢӨ. мҰү, 3-л¶„н• көҗм°Ё кІҖмҰқмқ„ м Ғмҡ©н•ҳмҳҖмңјл©°, лӘЁл“ н•ҳмң„ 집합мқ„ нӣҲл Ё 집합мңјлЎң л§Ңл“Ө л•Ңк№Ңм§Җ л°ҳліөн•ҳм—¬ к°Ғ мӢңн–үл§ҲлӢӨ лӘЁлҚёмқҳ м„ұлҠҘмқ„ кі„мӮ°н•ҳмҳҖлӢӨ. k-NN, SVM, Random forestмқҳ к°Ғ мҙҲл§Өк°ңліҖмҲҳмҷҖ мөңм Ғнҷ” кІ°кіјлҘј Table 3,4,5м—җ м •лҰ¬н•ҳмҳҖлӢӨ. м—¬кё°м„ң, SVMмқҳ CмҷҖ GammaлҠ” к°Ғк°Ғ мҳӨлҘҳ н—Ҳмҡ© ліҖмҲҳ л°Ҹ кІ°м • кІҪкі„мқҳ ліөмһЎлҸ„мҷҖ кҙҖл Ёлҗң ліҖмҲҳмқҙлӢӨ. Random forestмқҳ n_estimators, max_depthлҠ” к°Ғк°Ғ кІ°м • нҠёлҰ¬ к°ңмҲҳ л°Ҹ мөңлҢҖ к№ҠмқҙлҘј мқҳлҜён•ңлӢӨ.
мқҙмғҒк°җм§Җм—җлҠ” лЁјм Җ кё°кі„н•ҷмҠө лӘЁлҚёмқ„ м Ғмҡ©н•ҳмҳҖлӢӨ. fraw, fChi, fPCA мқҳ нҠ№м§• лІЎн„°лҘј н•ҷмҠөм—җ мӮ¬мҡ©н•ҳмҳҖмңјл©°, м„ёк°Җм§Җ мў…лҘҳмқҳ кі мһҘ мӢ нҳём—җ мқҙмғҒ л Ҳмқҙлё”мқ„ м§Җм •н•ҳмҳҖлӢӨ. Table 6м—җ к°Ғ м•Ңкі лҰ¬мҰҳкіј н•ҷмҠө лІЎн„° лі„лЎң мҳҲмёЎ м„ұлҠҘмқ„ м •лҰ¬н•ҳмҳҖлӢӨ. frawлЎң н•ҷмҠөн•ҳмҳҖмқ„ л•Ң 분лҘҳ м•Ңкі лҰ¬мҰҳмқҳ мқҙмғҒ к°җм§Җ м„ұлҠҘмқҙ к°ҖмһҘ лҶ’кі fPCAлҠ” м•Ҫк°„ лӮ®мқҖ м„ұлҠҘмқ„ ліҙмҳҖмңјлӮҳ, м •нҷ•м„ұ м°ЁмқҙлҠ” нҒ¬м§Җ м•ҠмқҢмқ„ нҷ•мқён•ҳмҳҖлӢӨ.
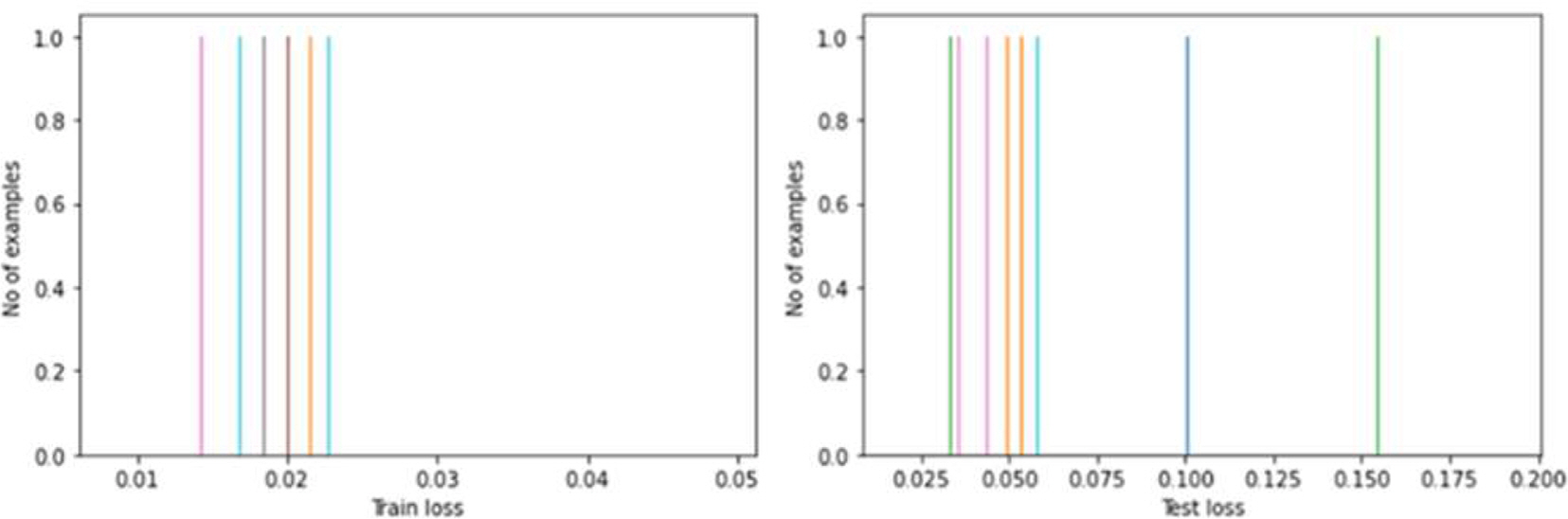
лӢӨмқҢмңјлЎң мҳӨнҶ мқёмҪ”лҚ”лҘј м Ғмҡ©н•ҳм—¬ мқҙмғҒ к°җм§ҖлҘј мҲҳн–үн•ҳмҳҖмңјл©°, н•ҷмҠөмқҳ мһ…л Ҙ мёөмңјлЎң frawлҘј мӮ¬мҡ©н•ҳмҳҖлӢӨ. лӢЁ, м •мғҒ мғҳн”Ңкіј л№„м •мғҒ мғҳн”Ңмқҳ 비мңЁмқҙ 245:4,155мңјлЎң л¶Ҳк· нҳ•мқҙ мӢ¬н•ҳмҳҖмңјлҜҖлЎң SMOTE кё°лІ•(Chawla et al., 2002)мқ„ мӮ¬мҡ©н•ҳм—¬ кіјм„ нғқ (Over sampling)мқ„ мӢӨмӢңн•ҳмҳҖлӢӨ. л§Өк°ң ліҖмҲҳлҠ” sampling strategy=auto, k_neighbors=5, random stateлҘј м„ нғқн•ҳкі , Sampling_strategy=not majorityлЎңмҚЁ лӢӨмҲҳнҒҙлһҳмҠӨм—җ л§һм¶° н•ҳмң„ нҒҙлһҳмҠӨлҘј кіјм„ нғқ н•ҳмҳҖлӢӨ. SMOTEмқ„ м Ғмҡ©н•ң кІ°кіј м •мғҒкіј л№„м •мғҒ мғҳн”Ңмқҳ 비мңЁмқ„ 4,155:4,155лЎң кө¬м„ұлҗҳм—ҲлӢӨ. мһ¬мғқм„ұ мҳӨм°Ё к°’мқҖ MAEлҘј мӮ¬мҡ©н–Ҳмңјл©°, Fig. 8мқҖ к°Ғк°Ғ м •мғҒ мғҳн”Ңкіј мқҙмғҒ мғҳн”Ңмқ„ н•ҷмҠөмӢңмј°мқ„ л•Ң кі„мӮ°лҗң мһ¬мғқм„ұ мҳӨм°Ёмқҳ нһҲмҠӨнҶ к·ёлһЁмқҙлӢӨ. м •мғҒ мғҳн”Ңкіј мқҙмғҒ мғҳн”Ңмқҳ MAEк°’мқҖ к°Ғк°Ғ 0.014~0.023кіј 0.03~0.155мқҳ 분нҸ¬лҘј ліҙмҳҖлӢӨ. мһ„кі„м җмқҖ м •мғҒ мғҳн”Ңмқҳ MAE нҸүк· к°’м—җ 2л°°мқҳ н‘ңмӨҖнҺём°ЁлҘј лҚ”н•ҙ 0.03лЎң м„Өм •н–Ҳмңјл©°, мһ„кі„м җмқ„ мҙҲкіјн•ҳлҠ” MAEлҘј мғқм„ұн•ҳлҠ” мғҳн”Ңмқ„ л№„м •мғҒ мғҒнғңлЎң 분лҘҳн–ҲлӢӨ. мҳӨнҶ мқёмҪ”лҚ” кё°л°ҳ мқҙмғҒк°җм§Җ лӘЁлҚёмқҳ мқҙмғҒк°җм§Җ м„ұлҠҘмқҖ Table 7мҷҖ к°ҷмқҙ кі„мӮ°лҗҳм—ҲлӢӨ.
ліё м ҲмқҖ кё°кі„н•ҷмҠөкіј н•©м„ұкіұ м•Ңкі лҰ¬мҰҳмқ„ м Ғмҡ©н•ң кі мһҘ мҳҲмёЎ кІ°кіјлҘј м •лҰ¬н•ҳмҳҖлӢӨ. Table 8м—җ м•Ңкі лҰ¬мҰҳ лі„ кі мһҘ진лӢЁ м •нҷ•лҸ„лҘј м •лҰ¬н•ҳмҳҖмңјл©°, нҠ№м§• лІЎн„° frawк°Җ лӘЁл“ м•Ңкі лҰ¬мҰҳ лӮҙм—җм„ң к°ҖмһҘ мҡ°мҲҳн•ң мҳҲмёЎ м„ұлҠҘмқ„ ліҙм—¬мЈјм—ҲлӢӨ. м„ұлҠҘ нҸүк· мқҖ Random forest(99.79%), SVM(99.78%), k-NN(99.42%) мҲңмңјлЎң кі„мӮ°лҗҳм—ҲлӢӨ.
лӢӨмқҢмңјлЎң, Conv1DлЎң кі мһҘ진лӢЁ лӘЁлҚёмқ„ кө¬м„ұн•ҳмҳҖмңјл©°, к°Ғ м Ғмёө кө¬мЎ°лҘј Table 9м—җ м •лҰ¬н•ҳмҳҖлӢӨ. 진лҸҷ мӢ нҳём—җ м ҖмЈјнҢҢ нҶөкіј н•„н„°лҘј мӮ¬мҡ©н•ҳкі , 1.0 kHzлЎң лӢӨмҡҙ мғҳн”Ңл§Ғн•ҳм—¬ мһ…л Ҙ мёөмңјлЎң мӮ¬мҡ©н•ҳмҳҖлӢӨ. Conv1DлҠ” 99.55%мқҳ нҸүк· м„ұлҠҘмңјлЎң кі мһҘмқ„ к°җм§Җн•ҳмҳҖлӢӨ. Random ForestмҷҖ SVM лӘЁлҚёмқҳ 분лҘҳ м„ұлҠҘмқҙ Conv1D лӘЁлҚёліҙлӢӨ мҡ°мҲҳн•ҳмҳҖмңјлӮҳ, к°’мқҳ м°ЁмқҙлҠ” нҒ¬м§Җ м•ҠмқҢмқ„ м•Ң мҲҳ мһҲлӢӨ. л”°лқјм„ң ліҖлҸҷ мҶҚлҸ„лҘј к°Җ진 нҡҢм „кё°кё°мқҳ кі мһҘ진лӢЁм—җм„ң мЈјнҢҢмҲҳ мҶҚм„ұмқ„ нҠ№м§•м—җ нҸ¬н•Ён•ңлӢӨл©ҙ, кё°кі„н•ҷмҠөлҸ„ н•©м„ұкіұ м•Ңкі лҰ¬мҰҳкіј лҸҷл“ұн•ң мҲҳмӨҖмқҳ м •нҷ•лҸ„лЎң 진лӢЁн• мҲҳ мһҲмқҢмқ„ нҷ•мқён• мҲҳ мһҲм—ҲлӢӨ. Conv1D л°©лІ•мқҖ лҲ„м Ғлҗң кі„мёЎ мӢ нҳёлҘј н•ҷмҠөн•ҳлҠ” кіјм •м—җ л§ҺмқҖ м—°мӮ° мӢңк°„мқҙ н•„мҡ”н•ң л°ҳл©ҙм—җ кё°кі„н•ҷмҠөмқҖ мӨҖ비лҗң н•ҷмҠөмһҗк°Җ мӢӨмӢңк°„м—җ к°Җк№қкІҢ 진лӢЁмқ„ мҲҳн–үн• мҲҳ мһҲлҠ” мһҘм җмқҙ мһҲлӢӨлҠ” м җмқ„ к°җм•Ҳн•ҳл©ҙ, м Ғм Ҳн•ң нҠ№м§• лІЎн„°лҘј л°ҳмҳҒн•ң кё°кі„н•ҷмҠөмқҙ ліҖмҶҚмЎ°кұҙмқҳ кі мһҘ진лӢЁм—җ м Ғмҡ©лҗ мҲҳ мһҲмқҢмқ„ м•Ң мҲҳ мһҲлӢӨ.
ліё л…јл¬ём—җм„ңлҠ” ліҖлҸҷ мҶҚлҸ„лҘј к°Җ진 нҡҢм „кё°кё°мқҳ мқҙмғҒ 진лӢЁ л°Ҹ кі мһҘ진лӢЁ мҳҲлҘј м ңмӢңн•ҳмҳҖлӢӨ. ліҖлҸҷ мҶҚлҸ„ мЎ°кұҙн•ҳм—җ мӢӨн—ҳлҗң кі мһҘ мӢң뮬л Ҳмқҙн„°мқҳ лҚ°мқҙн„°лҘј н•ҷмҠө лҢҖмғҒмңјлЎң мӮ¬мҡ©н•ҳмҳҖлӢӨ. мқҙмғҒк°җм§Җм—җм„ңлҠ” мҳӨнҶ мқёмҪ”лҚ”к°Җ кё°кі„н•ҷмҠөліҙлӢӨ м •нҷ•лҸ„к°Җ л–Ём–ҙмЎҢмңјлӮҳ, л№„м •мғҒ лҚ°мқҙн„°к°Җ м—ҶлҠ” кІҪмҡ°м—җлҠ” нҷңмҡ©н• мҲҳ мһҲлҠ” м •нҷ•м„ұмқ„ ліҙмқё кІғмңјлЎң нҢҗлӢЁлҗңлӢӨ. кі мһҘ 진лӢЁм—җлҠ” кё°кі„н•ҷмҠөкіј Conv1DлҘј м Ғмҡ©н•ҳм—¬ к°Ғк°Ғмқҳ м •нҷ•м„ұмқ„ 비көҗн•ҳмҳҖлӢӨ. мқҙ кіјм •м—җм„ң нҠ№м§• м„ нғқм—җм„ң мЈјнҢҢмҲҳ мҶҚм„ұмқ„ 추к°Җн•ЁмңјлЎңмҚЁ кё°кі„н•ҷмҠөмқҳ 진лӢЁ м •нҷ•лҸ„к°Җ Conv1Dмқҳ м„ұлҠҘкіј мң мӮ¬н•ҳкұ°лӮҳ лҚ” мҡ°мҲҳн• мҲҳ мһҲмқҢмқ„ м ңмӢңн•ҳмҳҖлӢӨ. нҠ№нһҲ, мЎ°нҷ”мЈјнҢҢмҲҳ лі„лЎң мғҒлҢҖм Ғ 진нҸӯ ліҖнҷ”лҘј нҠ№м§• лІЎн„°м—җ л°ҳмҳҒн•ҳм—¬ л№„м •мғҒм„ұмқҙ кі л Өлҗ мҲҳ мһҲмқҢмқ„ ліҙмҳҖлӢӨ. лӢӨл§Ң, мӢӨм ң мһҘ비лҠ” ліөмһЎн•ң мЎ°лҰҪ кө¬мЎ°лҘј к°Җм§җм—җ л”°лқј мӢ нҳём—җ мһЎмқҢмқҙ л§Һмңјл©°, нҡҢм „мҶҚлҸ„мҷҖ н•ҳмӨ‘мқҳ ліҖлҸҷмңјлЎң мқён•ҙ л№„м •мғҒм„ұмқҙ нӣЁм”¬ лҶ’мқҖ мӢ нҳёк°Җ кі„мёЎлҗ кІғмңјлЎң мҳҲмғҒлҗңлӢӨ. л”°лқјм„ң м ңм•Ҳлҗң м•Ңкі лҰ¬мҰҳмқ„ мӢӨм ң мҡҙмҳҒ мһҘ비м—җ м Ғмҡ©н•ҳкё° мң„н•ҙм„ңлҠ” мһЎмқҢ м ңкұ° л°©м•Ҳ, лҶ’мқҖ л№„м •мғҒм„ұмқ„ кі л Өн•ң м „мІҳлҰ¬ л°Ҹ м Ғм Ҳн•ң нҠ№м§• 추м¶ңмқҙ 추к°ҖлЎң н•„мҡ”н• кІғмңјлЎң нҢҗлӢЁлҗңлӢӨ.
Acknowledgments
ліё м—°кө¬лҠ” 2022л…„лҸ„ мӮ°м—…нҶөмӮ°мһҗмӣҗл¶Җ(н•ҙм–‘мҲҳмӮ°л¶Җ) л°Ҹ мӮ°м—…кё°мҲ нҸүк°ҖкҙҖлҰ¬мӣҗ(н•ҙм–‘мҲҳмӮ°кіјн•ҷкё°мҲ 진нқҘмӣҗ) м—°кө¬л№„ м§ҖмӣҗмңјлЎң мҲҳн–үлҗң вҖҳмһҗмңЁмҡҙн•ӯм„ л°• кё°мҲ к°ңл°ңмӮ¬м—… (20011164, мһҗмңЁмҡҙн•ӯм„ л°• н•өмӢ¬ кё°кҙҖмӢңмҠӨн…ң м„ұлҠҘ лӘЁлӢҲн„°л§Ғ л°Ҹ кі мһҘмҳҲмёЎ/진лӢЁ мӢңмҠӨн…ң кё°мҲ к°ңл°ңм—°кө¬)вҖҷмқҳ м—°кө¬кІ°кіјмһ…лӢҲлӢӨ.
TableВ 1.
Algorithms tried to anomaly detection and fault diagnosis
| Diagnosis procedure | Machine learning | Deep learning |
|---|---|---|
| Anomaly detection | k-NN, SVM, Random Forest | Autoencoder |
| Fault diagnosis | k-NN, SVM, Random Forest | CNN (Conv1D) |
TableВ 2.
Features extracted from MAFAULDA
| Domain | Features |
|---|---|
| Time domain | xabs, xrms, xskew, xkurt |
| Frequency domain | Amplitude of 1Fr, 2Fr, 3Fr |
TableВ 3.
Grid search bound of each algorithm and feature vector
TableВ 4.
Optimization result of hyper-parameter for each anomaly detection algorithm and feature vector
TableВ 5.
Optimization result of hyper-parameter for each fault detection algorithm and feature vector
TableВ 6.
Performance of machine learning in anomaly detection
TableВ 7.
Performance of autoencoder-based anomaly detection model
| Score | Performance (%) |
|---|---|
| Accuracy | 92.84 |
| Precision | 95.84 |
| Recall | 89.56 |
| F1 | 92.60 |
TableВ 8.
Performance of machine learning-based fault detection
TableВ 9.
Layers of Conv1D applied to fault detection
References
[1] Bartelmus, W, Chaari, F, Zimroz, R and Haddar, M(2010), вҖңвҖңModelling of gearbox dynamics under time-varying nonstationary load for distributed fault detection and diagnosisвҖқвҖқ, European Journal of Mechanics-A/Solids, Vol. 29, No. 4, pp. 637-646.

[2] Breiman, L(2001), вҖңвҖңRandom forestsвҖқвҖқ, Machine Learning, Vol. 45, No. 1, pp. 5-32.
[3] Bui, DT, Pradhan, B, Lofman, O, Revhaug, I and Dick, OB(2012), вҖңвҖңApplication of support vector machines in landslide susceptibility assessment for the Hoa Binh province (Vietnam) with kernel functions analysisвҖқвҖқ.
[4] Chawla, V, Bowyer, KW, Hall, LO and Kegelmeyer, WP(2002), вҖңвҖңSMOTE: synthetic minority over-sampling techniqueвҖқвҖқ, Journal of Artificial Intelligence Research, Vol. 16, pp. 321-357.

[5] Cover, T and Hart, P(1967), вҖңвҖңNearest Neighbor Pattern ClassificationвҖқвҖқ, IEEE Transactions on Information Theory, Vol. 13, No. 1, pp. 21-27.

[6] de Lima, AA and et al(2013), вҖңвҖңOn fault classification in rotating machines using fourier domain features and neural networksвҖқвҖқ, In 2013 IEEE 4th Latin American Symposium on Circuits and Systems (LASCAS), IEEE, pp. 1-4.
[7] Faust, O, Hagiwara, Y, Hong, TJ, Lih, O. S. and Acharya, UR(2018), вҖңвҖңDeep learning for healthcare applications based on physiological signals: A reviewвҖқвҖқ, Computer methods and programs in biomedicine, Vol. 161, pp. 1-13.


[8] Feng, Z and Liang, M(2014), вҖңвҖңFault diagnosis of wind turbine planetary gearbox under nonstationary conditions via adaptive optimal kernel time-frequency analysisвҖқвҖқ, Renewable Energy, Vol. 66, pp. 468-477.

[9] Kan, MS, Tan, AC and Mathew, J(2015), вҖңвҖңA review on prognostic techniques for non-stationary and non-linear rotating systemsвҖқвҖқ, Mechanical Systems and Signal Processing, Vol. 62, pp. 1-20.

[10] Lee, JH(2021), вҖңвҖңExperimental Study on Application of an Anomaly Detection Algorithm in Electric Current Datasets Generated from Marine Air Compressor with Time-series FeaturesвҖқвҖқ, Journal of the Korean Society of Marine Environment & Safety, Vol. 27, No. 1, pp. 127-134.

[11] Li, W, Zhu, Z, Jiang, F, Zhou, G. and Chen, G(2015), вҖңвҖңFault diagnosis of rotating machinery with a novel statistical feature extraction and evaluation methodвҖқвҖқ, Mechanical Systems and Signal Processing, Vol. 50, pp. 414-426.

[12] Liao, Y, Huang, R, Li, J, Chen, Z and Li, W(2020), вҖңвҖңDeep semisupervised domain generalization network for rotary machinery fault diagnosis under variable speedвҖқвҖқ, IEEE Transactions on Instrumentation and Measurement, Vol. 69, No. 10, pp. 8064-8075.

[13] Pestana-Viana, D, Zambrano-LГіpez, R, de Lima, AA, Prego, T. D. M., Netto, S. L. and da Silva, EA(2016), вҖңвҖңThe influence of feature vector on the classification of mechanical faults using neural networksвҖқвҖқ, In 2016 IEEE 7th Latin American Symposium on Circuits & Systems (LASCAS), IEEE, pp. 115-118.

[14] Qiao, M, Yan, S, Tang, X and Xu, C(2020), вҖңвҖңDeep convolutional and LSTM recurrent neural networks for rolling bearing fault diagnosis under strong noises and variable loadsвҖқвҖқ, IEEE Access, Vol. 8, pp. 66257-66269.

[15] Refaeilzadeh, P, Tang, L and Liu, H(2009), вҖңвҖңCrossvalidationвҖқвҖқ, Encyclopedia of database systems, Vol. 5, pp. 532-538.

[16] Riaz, S, Elahi, H, Javaid, K and Shahzad, T(2017), вҖңвҖңVibration feature extraction and analysis for fault diagnosis of rotating machinery- a literature surveyвҖқвҖқ, Asia Pacific Journal of Multidisciplinary Research, Vol. 5, No. 1, pp. 103-110.
[17] Tao, H, Wang, P, Chen, Y, Stojanovic, V and Yang, H(2020), вҖңвҖңAn unsupervised fault diagnosis method for rolling bearing using STFT and generative neural networksвҖқвҖқ, Journal of the Franklin Institute, Vol. 357, No. 11, pp. 7286-7307.

[18] Verstraete, D, Ferrada, A, Droguett, EL, Meruane, V and Modarres, M(2017), вҖңвҖңDeep learning enabled fault diagnosis using time-frequency image analysis of rolling element bearingsвҖқвҖқ, Shock and Vibration, 2017.

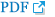
[19] Wang, B, Zhang, X, Xing, S, Sun, C and Chen, X(2021), вҖңвҖңSparse representation theory for support vector machine kernel function selection and its application in high-speed bearing fault diagnosisвҖқвҖқ, ISA transactions, Vol. 118, pp. 207-218.


[20] Wang, SH2019. вҖңPartial Discharge Detection in Power Line using 1D Convolutional Neural NetworkвҖқ, Hanyang University, Graduate school, Master thesis.
- TOOLS




 PDF Links
PDF Links PubReader
PubReader ePub Link
ePub Link Full text via DOI
Full text via DOI Download Citation
Download Citation Print
Print