1. 서 론
최근 4차 산업의 발달과 함께 IT 기술을 접목하여 차세대 수중드론을 통해 수중환경을 모니터링 하는 기술이 개발되고 있으며, 이러한 기술은 양식장을 원격으로 자동관리 하는 스마트 양식에도 응용되고 있다(Yun, 2021; YONHAP NEWS, 2019). 수중환경을 모니터링을 통한 스마트 양식 기술의 핵심 분야는 IoT (Internet of Thing) 기반 원격 모니터링 기술이다(Yun et al., 2010; Kaushal et al., 2016). IoT 기반 원격 수중모니터링 기술은 양식장 환경 상태를 동영상을 통해 원격으로 실시간 모니터링 하는 기술, 수중 영상을 통해 어류의 크기와 무게를 추정하는 기술 및 수온·용존산소·염분등을 실시간 모니터링 하여 양식환경의 변화가 발생하는 경우, 이를 자동으로 조절하는 기술이 있다(Yun, 2021). 이러한 스마트 양식 기술을 구현하기 위해 필요한 장치는 양식장 내를 이동하며 실시간으로 양식장의 상태를 관찰하고 양식장 데이터를 실시간으로 전송해 주는 장치가 필요하며, 소형의 수중드론은 양식장 내를 이동하면서 대규모 양식장의 상태를 실시간으로 관찰하기 위한 가장 효과적인 장치이다(Yun, 2020a; Yun, 2020b). 차세대 수중드론 기술을 구현하면 양식장의 용존산소, 수온, 염도, 탁도등의 환경 인자를 실시간으로 관찰할 수 있으며, 카메라를 통해 촬영한 실시간 동영상을 스마트폰 등의 모니터링 기기에 통해 전송할 수 있다. 양식장 환경 데이터는 드론에 부착된 센서를 통해 수집되며, 수중 동영상은 드론에 부착된 카메라를 통해 촬영된다. 이러한 수중 데이터와 동영상을 스마트폰등의 모니터링 기기로 전송하기 위해서는 무선통신을 위한 RF 단말기가 수중드론에 부착되어야 한다. Fig. 1은 최근 개발 중인 수중드론을 구성하는 IT 시스템을 보여준다(Yun, 2021). 그림에서 보는 바와 같이 수중드론은 4개의 시스템으로 구성되며, 구체적으로 용존산소, 수온, 염도, 탁도등을 측정하는 센서, 수중 동영상 촬영을 위한 카메라모듈, 수중데이터 및 동영상을 디지털 신호로 변환하는 베이스밴드 신호처리부, 수중데이터와 동영상을 스마트폰등의 모니터링 기기로 무선으로 전송하는 RF 단말기로 구성된다. 그런데, 양식장 환경은 직경이 수십 m 정도로 공간이 협소하므로 소형의 드론이 사용되어야 하며, 상용화된 베이스밴드 신호처리 시스템과 RF 단발기는 소형드론에 부착하기에는 너무 무거우며 사이즈가 너무 크다(Yun, 2021). 따라서, 현재의 기술로는 수중데이터와 수중동영상을 실시간으로 전송하는 차세대 수중드론을 개발하기에는 한계가 있다.
최근 Fig. 1의 베이스밴드 신호처리부를 모두 포함한 시스템을 FPGA (Field Programmable Gate Array) 기술을 이용하여 실리콘 반도체상에 CMOS (Complementary Metal-Oxide Semiconductor) chip으로 개발하려는 연구가 진행되고 있다(Yun, 2020a; Yun, 2020b). 따라서, 베이스밴드 신호처리 시스템에 대한 1 chip SoC (System on Chip)화를 통한 소형화 및 경량화는 빠른 시일 내에 구현이 가능하나, RF 단말기의 SoC 화를 통한 소형화를 위해서는 아래의 두 가지 문제점을 해결해야 한다.
첫 번째 문제점은 다음과 같다. 무선통신 부품 중에서 길이가 λ/4인 전송선로를 기반으로 하는 분배기 및 결합기등은 무선통신 회로 내에서 아주 큰 점유면적을 가진다. 따라서, 이러한 RF 수동소자들은 반도체 기판 상에 집적되지 못하고 실리콘 반도체 외부의 PCB 기판 상에 제작되고 있으며 이는 RF 단말기의 소형화 및 경량화에 큰 걸림돌이 되고 있다 (Basset et al., 2021; Lee et al., 2006).
그리고, 두 번째 문제점은 저임피던스 선로를 구현하기 위해서 종래의 전송선로를 이용하는 경우 선로 폭이 너무 커서 실리콘 반도체상에 집적이 불가능하다는 것이다. 실리콘 반도체상에서 능동소자로 사용되는 트랜지스터는 높은 주파수대역에서는 보통 20 Ω이하의 낮은 임피던스 값을 보이며, 회로구성을 간략화 하여 정합소자의 수를 줄이기 위해서는 트랜지스터의 입출력 부분에 20 Ω이하의 낮은 임피던스를 가지는 정합소자를 배치해야 한다 (Yun, 2017; Yun, 2018). 그러나, 실리콘 기판 상에 제작된 종래의 전송선로를 이용하는 경우10 GHz에서 파장이 10.2 mm이며, 20 Ω이하의 특성임피던스를 가지는 선로를 제작하기 위해서는 선로 폭이 3 mm이상이 되어야 한다 (Yun, 2017; Pozar, 1990). 따라서, 실리콘 기판상에서 종래의 전송선로를 사용하여 짧은 파장 및 낮은 임피던스 특성을 가지는 전송선로를 제작하는 경우, 큰 점유면적으로 실리콘 반도체 내부에 집적하는 것이 불가능하다.
Fig. 1의 베이스밴드 신호처리부와 RF 단말기를 모두 소형의 수중드론에 부착하기 위해서는 이 시스템을 모두 통합한 1 chip FISoC (Fully-integrated system on chip)를 구현해야하며, 이를 위해서는 상기 두 가지 문제점이 해소된 RF용전송선로를 개발해야 한다. 이를 위해 최근 주기적 구조를 적용하여 면적축소를 구현한 전송선로에 대한 연구가 활발히 진행되고 있으며 (Kratzer et al., 2019; Pawan et al., 2019), 현재까지 발표된 연구 중 실리콘 반도체상에서 가장 적은 점유면적을 가지는 RF용 전송선로는 3D 결합구조를 가지는 코프레너 선로인 CWP3DCS (coplanar waveguide employing periodic 3D coupling structures)이다 (Yun, 2017; Yun, 2018). CWP3DCS는 종래의 전송선로에 비해 파장의 길이가크게 줄어들었으며, 이로 인해 실리콘 반도체 기판 상에서의 점유면적이 크게 줄어들었으며 RF용 전송선로로서의 응용가능성을 보여주었다. 그러나, 반도체 기판 상에서 무선통신소자를 구현하기 위한 전송선로로써 사용되기 위해서는 대역폭 및 특성 임피던스에 대한 연구가 필요하나, CWP3DCS에 대한 3차원 결합구조의 복잡성에 의해 기존의 식과 해석방법(Pozar, 1990)으로는 해석이 불가능하다. 따라서, 현재까지 CWP3DCS에 대한 대역폭 및 임피던스 특성에 대한 해석이 이루어지지 못하고 있다.
이미 발표된 CWP3DCS에 대한 연구(Yun, 2017; Yun, 2018)와 비교하여 본 연구의 차별성은 다음 같다. 본 연구에서는 기존의 대역폭 및 임피던스 해석 식(Pozar, 1990)에 측정값을 반영한 measurement-based equation을 유도하여 CWP3DCS에 대한 대역폭 및 임피던스 특성해석을 최초로 시도하였다. 구체적으로는 삽입손실에 대한 측정값으로부터 CWP3DCS에 대한 3차원 결합용량을 추출하였으며, 추출된 용량 값을 기존의 대역폭 및 임피던스 해석 식에 반영한 measurement-based equation을 유도하였다. 해석결과에 의하면 CWP3DCS는 121 GHz까지 전송선로로써 사용이 가능하였으며, 20 μm의 선로 폭으로도 20 Ω이하의 낮은 임피던스를 가지는 전송선로의 구현이 가능하였으며, 동일한 임피던스를 가지는 선로 폭 이 3mm인 기존 전송선로(Pozar, 1990)에 비해 선로 폭이 크게 감소하였다. 그리고, 주기적 구조의 길이만 조절함으로써 원하는 특성임피던스를 가지는 선로를 쉽게 구현할 수 있었다. 그리고, CWP3DCS 구조의 경우 주파수 변화에 따른 특성 임피던스의 변화가 미미하므로 광대역 전송선로 및 광대역 분포정수형 수동소자에 이용될 수 있음을 알 수 있었다. 본 논문은 3D 결합구조를 가지는 코프레너 선로인 CWP3DCS의 대역폭에 대한 최초의 연구이다.
2. 3D 결합구조를 가지는 코프레너 선로구조 및 파장 특성
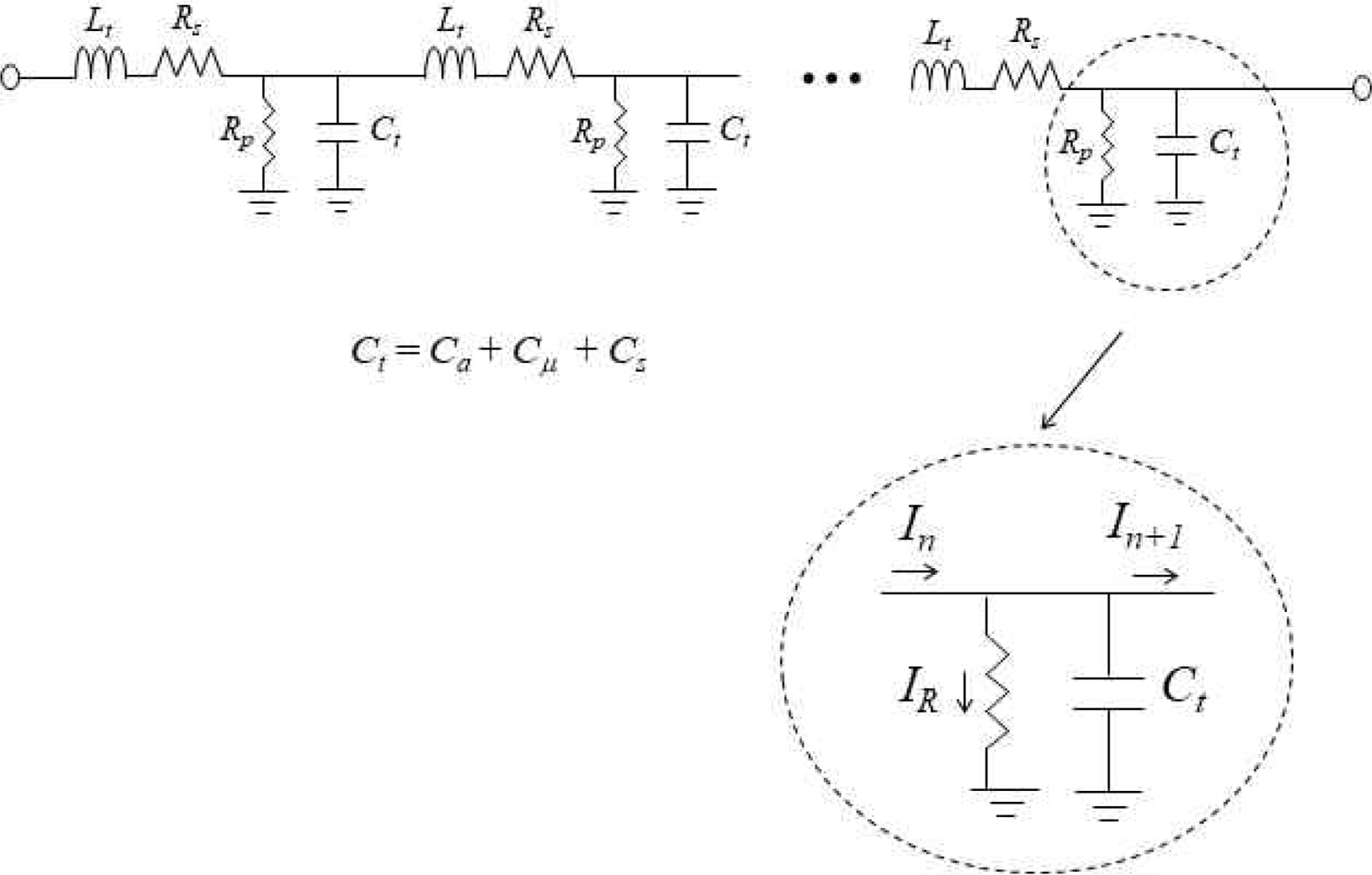
Fig. 2(a)와 (b)는 각각 CWP3DCS에 대한 구조와 LC 등가 회로이다. T 형태의 주기적인 스터브 구조인 TPMS (T-shape periodic metal strip)가 실리콘 기판 상에 위치하며, TPMS는 하부 선로구조인 LSL (lower signal line)에 접속되어 있다. 실리콘 기판상에 TPMS와 LSL로 이루어진 선로 구조체 양측에는 LGP (lower ground plane)이 존재하며, 최상부 면에는 USL (upper signal line)과 UGP (upper ground plane)가 위치한다. TPMS의 끝부분인 T형 머리부분은 UGP 아래에 위치한다. USL은 contact metal을 통하여 LSL에 전기적으로 연결되어 있으며, UGP은 LGP에 전기적으로 연결되어 있다. UGP와 TPMS사이에는 유전체 물질인 SiO2 박막이 위치하며, 이로 인해 UGP와 TPMS 사이에 커플링으로 인한 주기적인 용량 Cu가 존재한다. 종래의 코프레너 선로(Pozar, 1990)는 주기적 구조를 가지지 않으므로 Fig. 2(a)에서 보이는 USL과 UGP 사이에 존재하는 커플링 용량 Ca만 존재하지만, 본 연구에서 제안하는 선로구조는 Ca이외에도 추가적으로 UGP와 TPMS 사이의 커플링 용량 Cu가 존재한다. 그밖에도, 상기 선로구조의 경우 LGP와 TPMS 사이에도 전기적인 커플링이 발생하므로, Fig. 2(a)에서 보이는 바와 같이 추가적인 용량 CS도 존재한다.
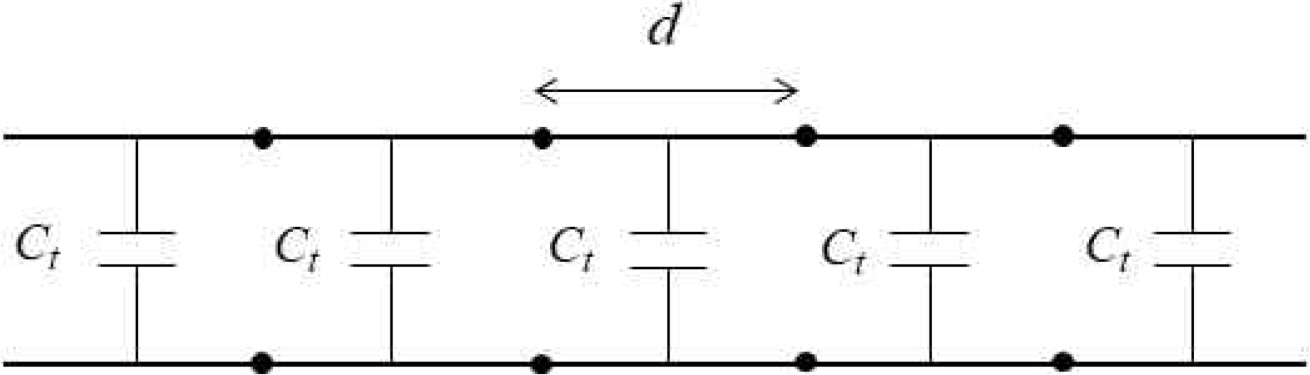
모든 RF용 저손실 전송선로는 등가의 LC 회로로 표현이 가능하므로(Pozar, 1990), 본 연구에서 제안하는 선로구조는 Fig. 2(b)에서 보이는 바와 같은 LC 등가회로로 나타낼 수 있다. 그림에서 Lt는 상기 전송선로에 대한 단위 길이당 주기적인 인덕턴스이다. 본 연구에서 제안하는 선로구조를 포함하여 모든 RF용 전송선로의 파장은 Fig. 2(b)로 표현되는 등가의 병렬 용량에 반비례하며, 다음 식으로 표현된다.
식(1)에서, f, L, C는 각각 중심주파수, 전송선로의 단위 길이 당 인덕턴스 값과 단위 길이당 용량 값이다. 식(1)에서 알 수 있는 바와 같이, 전송선로의 파장은 등가의 병렬 용량에 반비례하므로, 종래의 선로에 비해 높은 커플링 용량을 가지는 상기 선로구조는 종래의 코프레너 선로에 비해 짧은 파장 특성을 가지게 된다. 상기 선로구조의 경우 L=Lt이며, C=Ca+Cμ+Cs이다.
실리콘 기판상에 제작된 3D 결합구조를 가지는 코프레너 선로의 파장은 종래에 발표된 실리콘 기판상의 전송선로보다 훨씬 축소된 결과를 보여주었다 (Yun, 2017; Yun, 2018). 그 이유는, 종래의 코프레너 선로구조(Pozar, 1990)의 주기적인 등가용량은 Ca이나, 본 논문의 선로구조는 3D 결합구조에 의해 추가적인 용량 Cu와 CS도 존재하여 높은 등가용량을 가지게 되므로 식 (1)에 의해 단파장 특성을 보여줌을 추론 할 수 있다. Fig. 2(b)의 커패시터 병렬연결 구조로부터 알 수 있는 바와 같이 3D 결합구조를 가지는 코프레너 선로의 전체 주기적인 등가의 용량은 다음 식으로 표현된다.
결국 식 (2)로 표현되는 높은 전송선로 용량에 의해 식 (1)로부터 전송선로의 주기적 용량 값이 커지면 파장이 감소하게 됨을 알 수 있다.
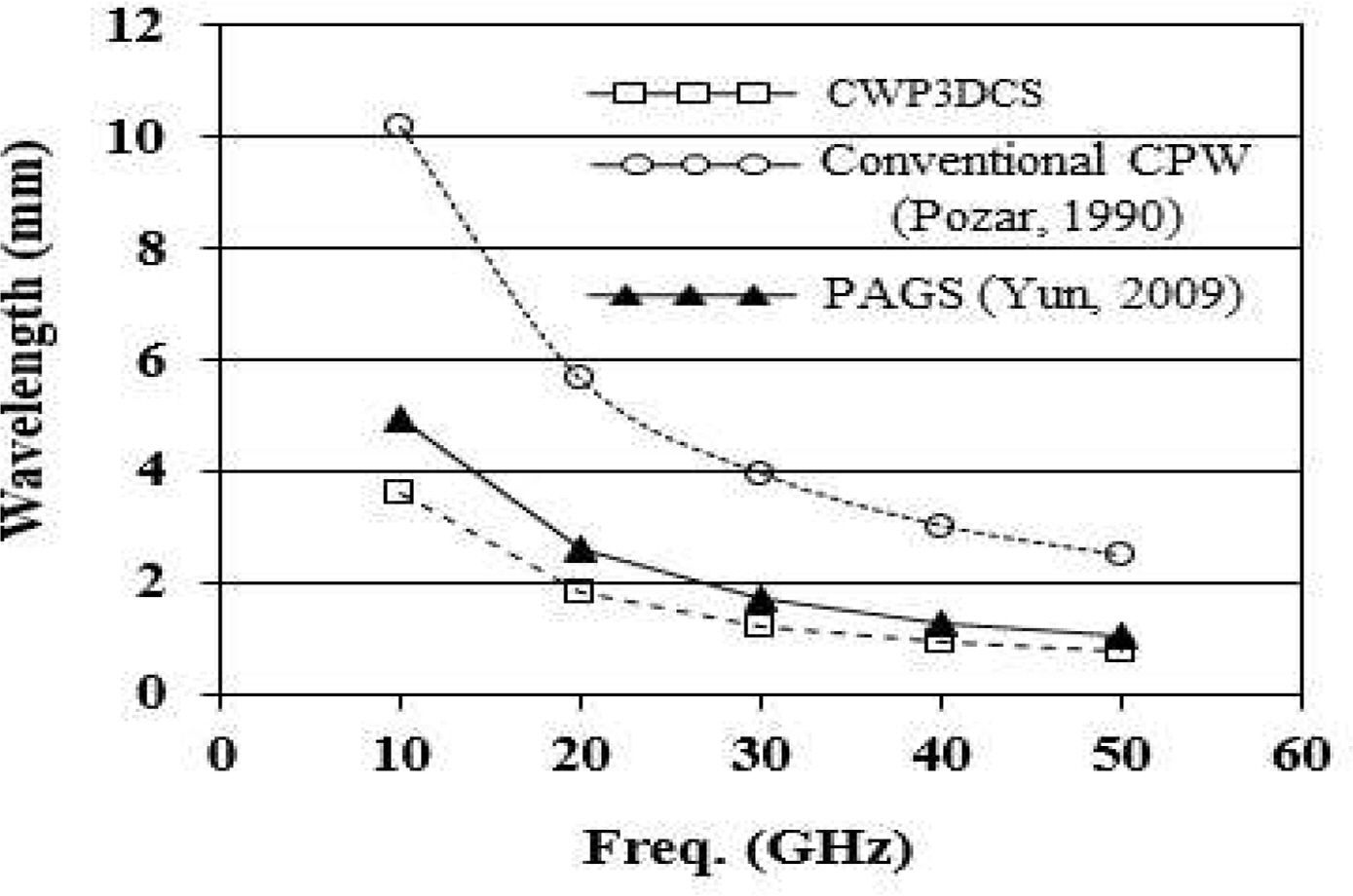
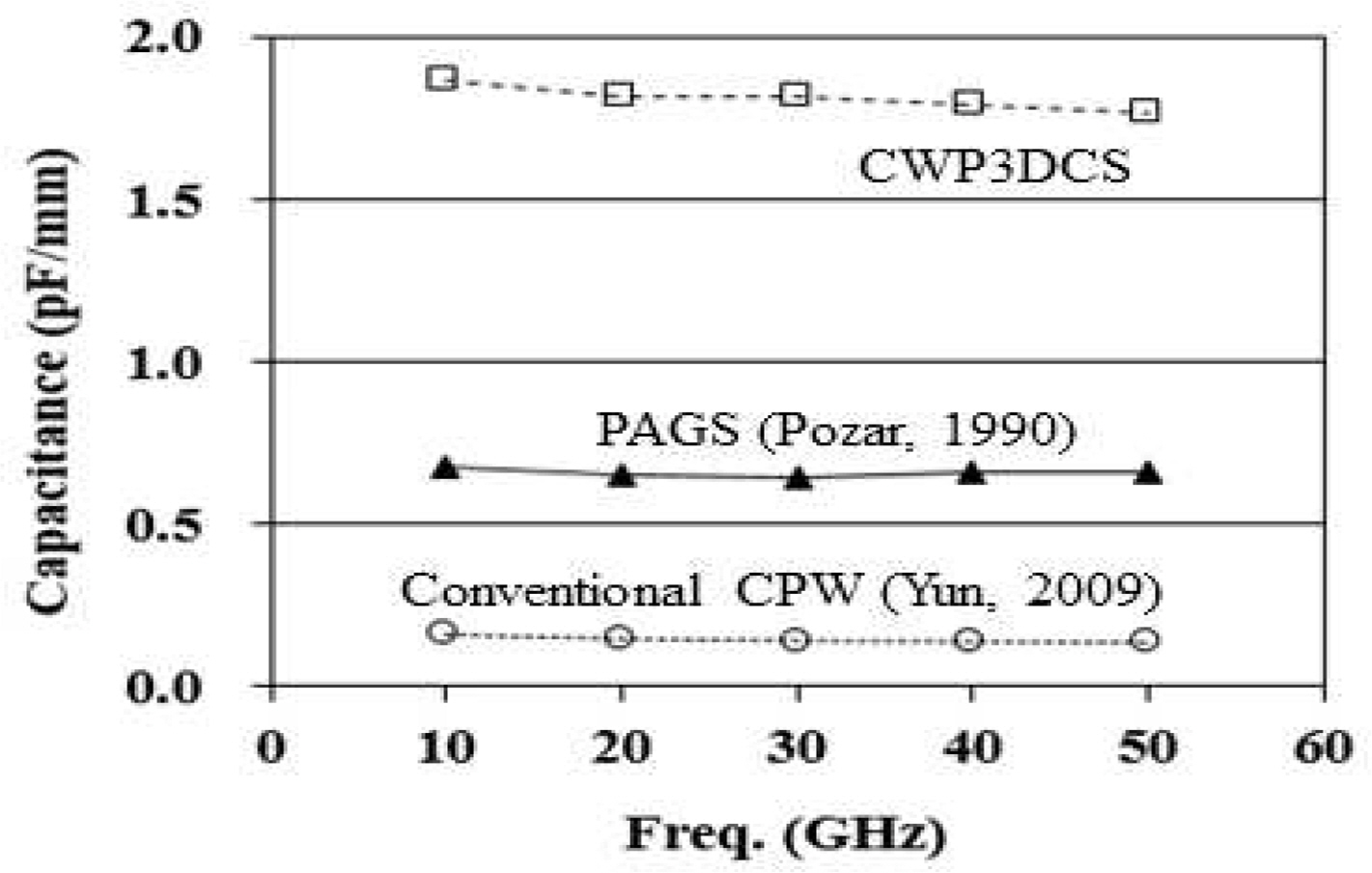
Fig. 3은 3D 결합구조를 가지는 코프레너 선로인 CWP3DCS에 대한 파장측정 결과를 보여준다. 비교를 위해 종래의 주기적인 전송선로 구조인 PAGS (periodically arrayed ground strip) 구조(Yun, 2009)와 주기적인 구조가 없는 종래의 코프레너 선로(Pozar, 1990)인 CPW의 파장 데이터도 추가되었다. Fig. 3에서 보는 바와 같이, CWP3DCS는 종래의 선로 구조보타 훨씬 짧은 파장특성을 보여준다. 구체적으로, 30 GHz에서 CWP3DCS의 파장은 1.225 mm이며, 이는 동일한 반도체 기판 상에서 제작된 종래의 코프레너 선로파장의 31.1%에 해당하는 수치이다. 상기 결과는 3D 결합구조를 가지는 코프레너 선로인 CWP3DCS를 이용하여 커플러 및 결합기등의 RF용 무선통신소자를 제작하면 반도체 기판상의 점유면적을 크게 축소할 수 있음을 의미한다.
3. 3D 결합구조를 가지는 코프레너 선로구조에 대한 measurement-based equation 식 유도와 이를 이용한 대역폭 및 특성 임피던스 해석
CWP3DCS에 대한 대역폭 및 임피던스 특성을 해석하기 위해서는 식 (2)로 표현되는 용량값 Ct값을 정확히 반영하는 수식이 필요하다. 그러나, Fig. 2(a)에서 보는 바와 같이 CWP3DCS에 대한 3차원 결합구조의 복잡성에 의해 기존의 대역폭 및 임피던스 해석 식(Pozar, 1990)을 이용하여 CWP3DCS에 대한 대역폭 및 임피던스 특성을 해석하는 것은 불가능하다. 따라서, 현재까지 CWP3DCS에 대한 대역폭 및 임피던스 특성에 대한 해석이 이루어지지 못하고 있다.
CWP3DCS에 대한 기존연구(Yun, 2017; Yun, 2018)와 비교한 본 연구의 차별성은 다음 같다. 본 연구에서는 기존의 대역폭 및 임피던스 해석 식(Pozar, 1990)에 삽입손실 측정값을 반영한 measurement-based equation을 유도하여 CWP3DCS에 대한 대역폭 및 임피던스 특성해석을 최초로 시도하였으며, 이에 대한 절차는 아래와 같다.
절차 1) 측정된 삽입손실 S21로부터 전송상수 β 추출
절차 2) 전송상수 β로부터 식 (2)로 표현되는 3차원 결합구조의 주기적인 용량 값 Ct 추출
절차 3) Ct 값을 반영한 대역폭에 관한 measurement-based equation을 유도
절차 4) 대역폭에 관한 measurement-based equation 정확도검증 및 measurement-based equation을 이용한 대역폭 특성해석
절차 5) Ct 값을 반영한 특성임피던스에 관한measurement-based equation을 유도
절차 6) 특성임피던스에 관한 measurement-based equation 정확도 검증 및 measurement-based equation을 이용한 임피던스 해석
3.1 측정된 삽입손실 S21로부터 전송상수 β값 추출
절차 1)에서 언급한 삽입손실 S21로부터 전송상수 β 추출하는 방법은 다음과 같다. 길이 l인 전송선로와 삽입손실의 관계는 다음과 같이 표현된다 (Pozar, 1990).
식(3)에서 ∠S21은 측정된 삽입손실 S21에 대한 위상각이며, degree로 표현된다. 상기 식을 radian으로 표현하면 다음과 같으며 아래의 식을 이용하여 측정된 삽입손실 S21로부터 전송 상수 β를 추출할 수 있다.
3.2 전송상수 β값으로부터 3차원 결합구조의 주기적인 용량 Ct값 추출
절차 2)에서 언급한 전송상수 β값으로부터 식 (2)로 표현되는 3차원 결합구조의 주기적인 용량 값 Ct 추출하는 방법은 다음과 같다. 모든 형태의 저손실 전송선로는 Fig. 2(b)과 같은 주기적인 LC 등가회로로 표현되며, 이와 같은 등가회로의 전송상수 β와 특성임피던스는 다음과 같이 표현된다(Pozar, 1990).
식 (5-1)과 (5-2)에서 ω는 각주파수이며, Lt와 Ct는 각각 Fig. 2(b)에서 보이는 CWP3DCS에 대한 주기적인 인덕턴스와 식 (2)로 표현되는 주기적인 용량이다. 상기 식으로부터 Ct는 다음과 같이 표현된다.
식 (4)와 (6)으로부터 Ct는 다음 식으로 표현되며, 결국 다음 식을 이용하여 측정된 삽입손실 S21로부터 Ct를 구할 수 있다.
식 (7)을 이용하여 Ct를 추출함으로써 측정값이 반영된 대역폭 및 특성임피던스 식을 구할 수 있다. Fig.4은 상기 식으로부터 추출한 Ct값을 보여준다. 그림은 T형 스터브의 길이 LT = 30 μm인 CWP3DCS에 대한 단위 길이당 주기적 용량 보여주며, 측정 데이터로부터 추출되었다. 비교를 위해 종래의 주기적인 전송선로 구조인 PAGS 구조와 주기적인 구조가 없는 종래의 코프레너 선로인 CPW의 데이터도 추가되었다. 600 μm 두께의 실리콘 반도체 기판 상에 선로가 제작 되었으며,선로 폭 WL는 20 μm 이다. 그리고, 주기적인 스터브 구조의 T형 머리부분의 폭 WT는 26 μm, 주기적인 스터브 구조사이의 거리는 20 μm이다. 유전체박막으로는 두께가 1 μm인 SiO2가 실리콘 반도체 기판 상에 증착되었다. 그림에서 보는 바와 같이 3D 결합구조를 가지는 코프레너 선로의 용량은 종래의 선로보다 훨씬 큰 값을 보여준다.
3.3 삽입손실 측정값으로부터 구한 Ct값을 반영한 대역폭에 관한 measurement-based equation 유도
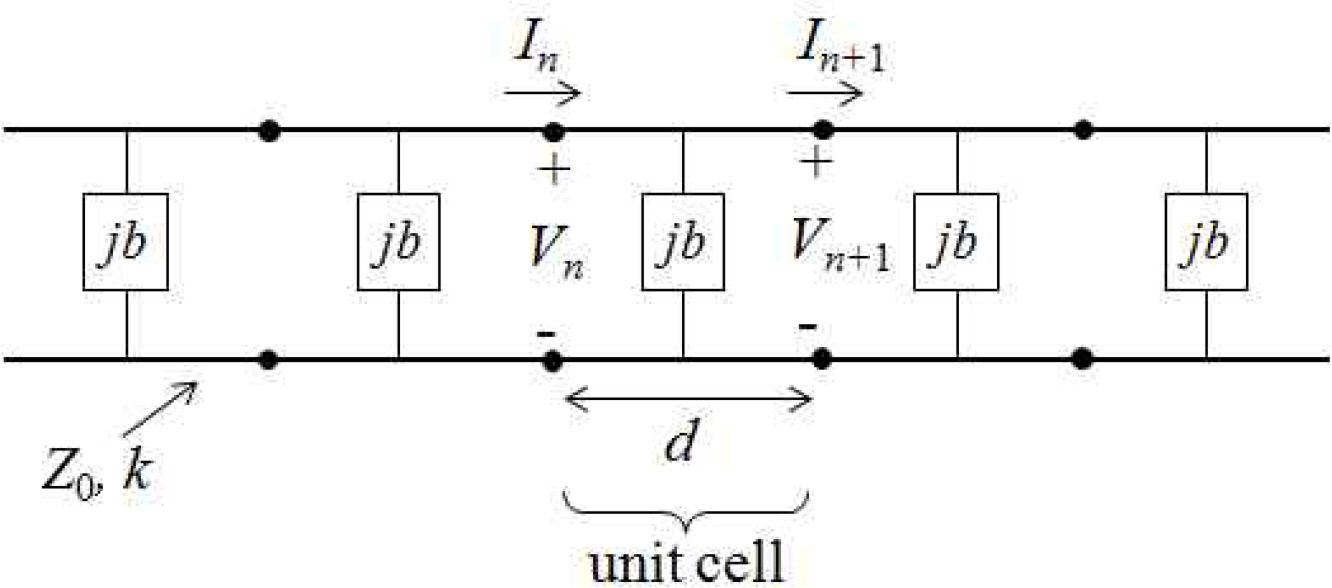
절차 3)에서 언급한 Ct 값을 반영한 대역폭에 관한 measurement-based equation애 대한 유도과정은 다음과 같다. Fig. 5와 같이 대역폭 및 임피던스를 계산하기 위하여 CWP3DCS 선로구조는 식 (7)로 표현되는 용량 Ct가 종단 된길이 d인 주기적 전송선로로 표현되었다. CWP3DCS 구조에서 주기적으로 존재하는 병렬 용량 Ct는 주기적인 세셉턴스 jb로 표현될 수 있으며, 다음 식과 같다.
식 (8)에서 ω는 동작주파수 f에 대한 각주파수 2πf이며, Z0는 주기적인 구조가 존재하지 않는 종래의 코프레너 선로에 대한 특성임피던스이며, Fig. 2(a)에서 보는 바와 같이 ST와 T는 각각 주기적인 구조 사이의 거리와 주기적인 구조의 폭이다. 상기 식 (8-1)과 (8-2)에 측정된 삽입손실로부터 추출한 용량 Ct가 포함되어 있다.
Fig. 6은 CWP3DCS 형태의 선로구조의 등가회로 상에 존재하는 전압 전류를 보여준다. 그림에서 b는 식 (8-2)로 표현되는 서셉턴스 값이다. 주기적 구조의 n번째 단위셀에 대한 입출력 전류 In, In+1과 입출력 전압 Vn, Vn+1은 ABCD 행렬에 의해 다음의 수식과 같이 표현 된다.
식 (9) 에서 μ0, ε0와 εe는 각각 공기에 대한 투자율, 유전율 및 주기적인 구조가 존재하지 않는 종래의 코프레너 선로에 대한 유효유전율이다. 본 논문의 주기적인 구조에 대한 전송 상수를 ϒ라고 가정하면 다음 식이 성립한다 (Pozar, 1990).
위의 방정식이 0이 아닌 근을 갖으며, 무손실 회로에서 AD-BC =1 임을 적용하여 방정식을 풀면, 다음과 같다.
주기적 구조 상에서의 전송 상수 ϒ는 손실성분을 가지므로 ϒ = α + β가 되어, 아래의 식이 성립 된다.
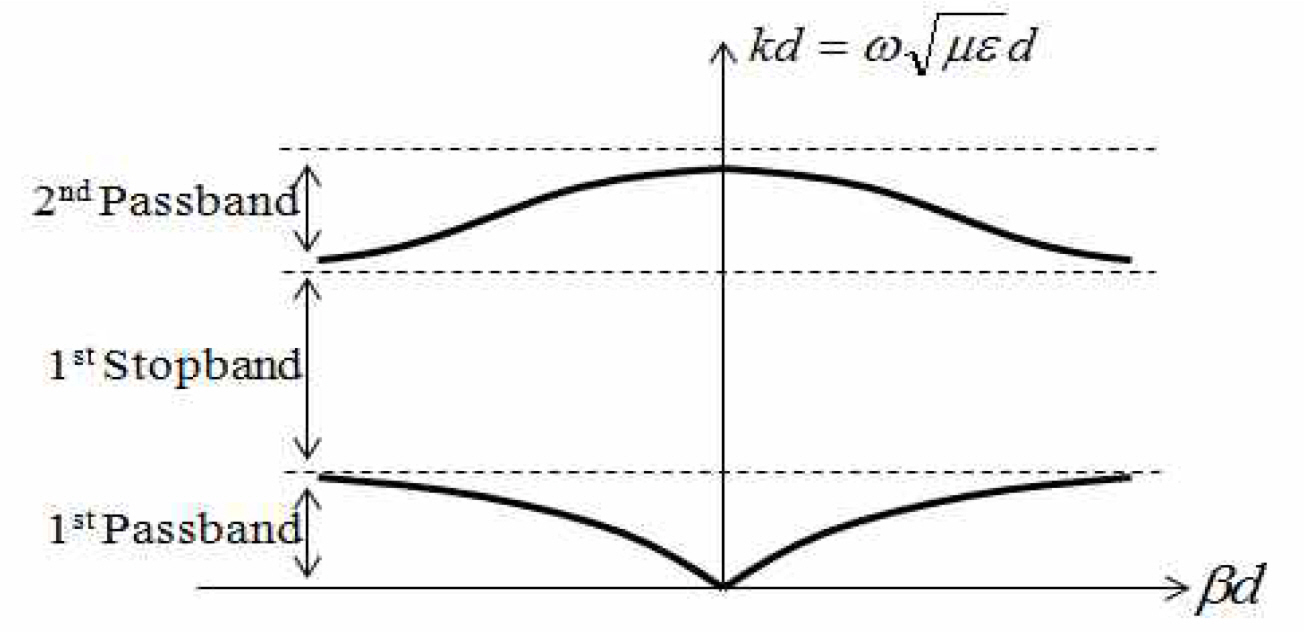
식 (13)을 통하여 α = 0, β ≠ 0일 때의 통과대역을 구할 수 있으며, α ≠ 0, β = 0일 때의 저지대역을 구할 수 있다.
통과대역과 저지대역을 구하는 수식은 아래의 각각 식과 같다.
식 (16)에서 변수 X에 측정된 삽입손실 S21로부터 추출한 용량 값 Ct가 포함되어 있으며, 식 (14)와 (15)가 대역폭에 관한 measurement-based equation이며, 이 식들을 이용하여 CWP3DCS의 대역폭을 추출할 수 있다.
3.4 대역폭에 관한 measurement-based equation 정확도 검증 및 식을 이용한 대역폭 특성 해석
절차 4)에서 언급한 대역폭에 관한 measurement-based equation 정확도 검증 및 대역폭 특성 해석내용은 다음과 같다. 식 (14)로부터 통과대역의 전송상수 β값은 다음과 같이 표현된다.
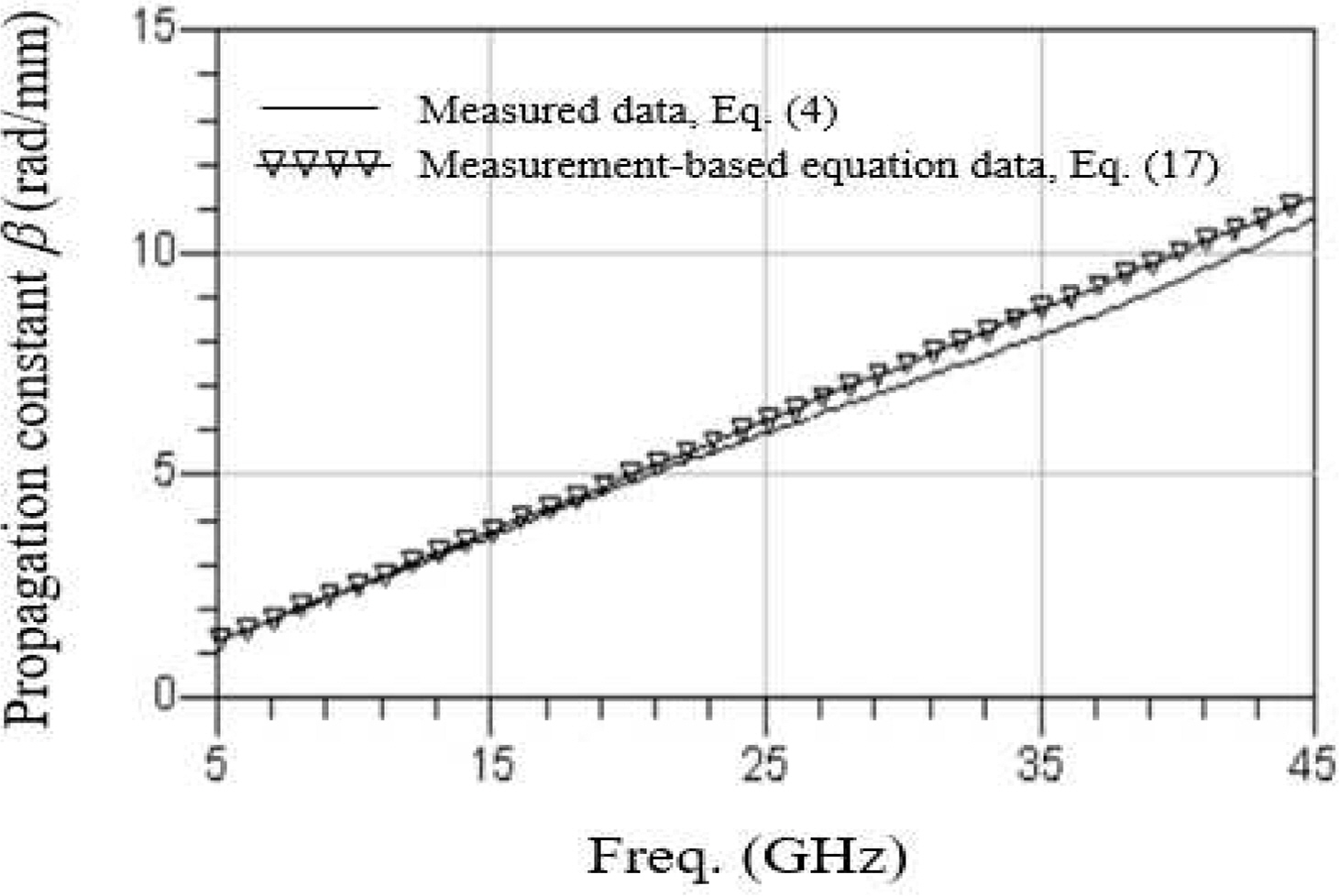
식 (17)에서 변수 X에 측정된 삽입손실 S21로부터 추출한 용량 값 Ct가 포함되어 있으며, 상기 식은 β에 대한 measurement-based equation가 된다. 전송선로의 대역폭은 보통 수백 GHz 대역이므로 대역폭을 정확하게 측정하는 것은 불가능하며, 따라서, 본 연구에서는 measurement-based equation을 이용하여 대역폭을 추출하였다. 대역폭에 대한 measurement-based equation의 정확도를 검증하기 위해서 식 (4)를 이용하여 추출된 β에 대한 측정값과 measurement-based equation인 식 (17)로부터 구한 β값을 비교하였다. Fig. 7은 식 (4)와 식 (17)로부터 구한 β값을 보여준다. Fig. 7에서 보는 바와 같이 측정값과 계산값이 잘 일치하는 것을 알 수 있으며, 최대오차는 6.4%이다.
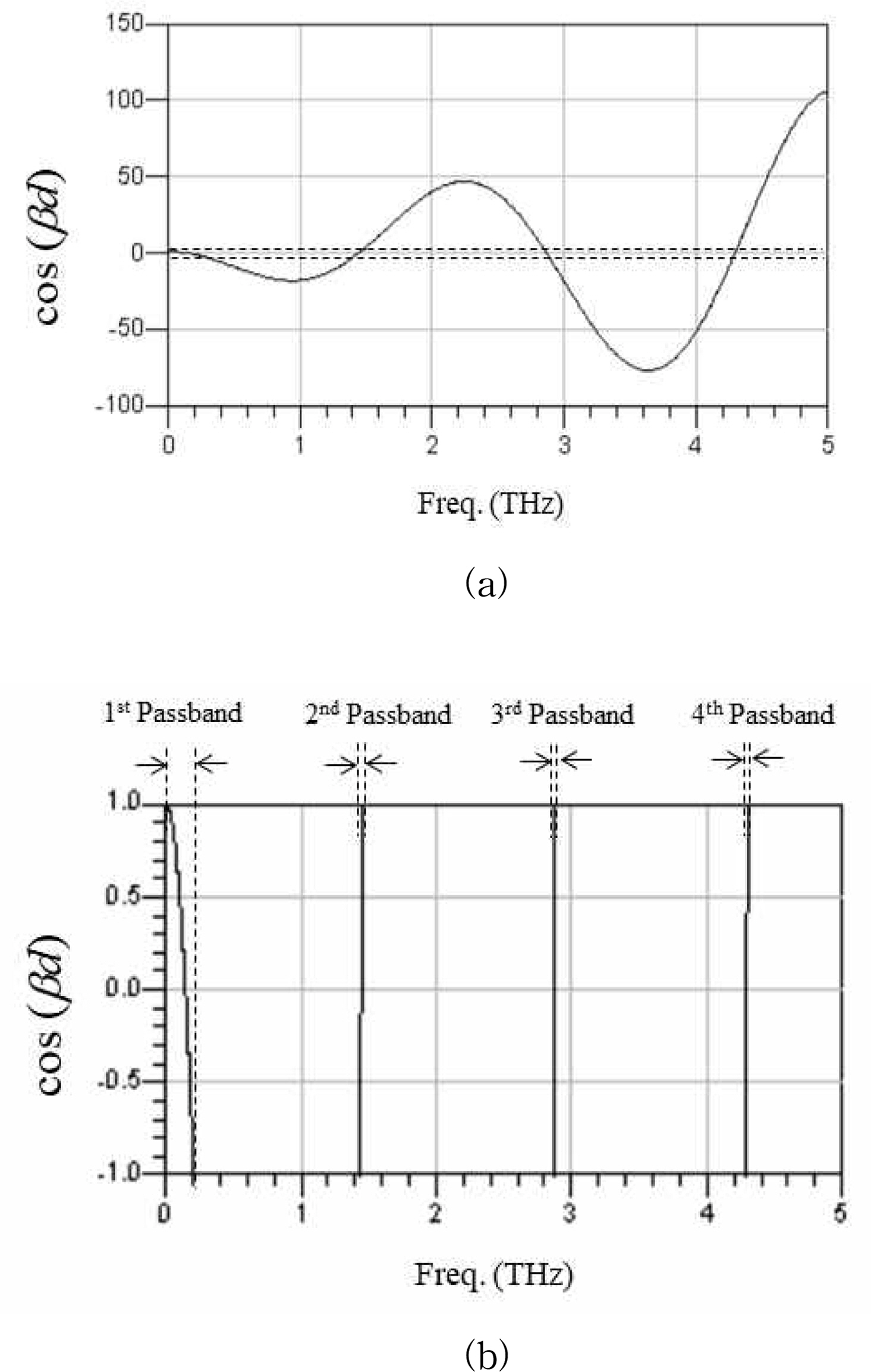
식 (14)의 passband 식에서 좌변의 |cos(βd)| < 1이므로, 식 (14)의 우변의 |cosd Xdsind| < 1인 구간은 전송상수가 존재하므로 통과대역이며, |cosd Xdsind| ≥ 1인 구간은 저지대역이다. Fig. 8(a), (b)는 LT = 30 μm인 CWP3DCS 선로구조에 대한 cos(βd)값의 주파수 특성이다. Fig. 8(a)는 cos(βd)값의 전체범위를 출력한 그래프이며, 점선으로 표시한 부분이 |cos(βd)| < 1인 구간에 해당하며, 이 부분을 확대한 그래프는 Fig. 8(b)에 나타내었다. 그림에서 보는바와 같이 |cos(βd)| < 1인 구간에 해당하는 주파수 범위가 passband에 해당되며, 이는 식 (14)에서 passband에 해당하는 영역이 좌변의|cos(βd)| < 1이기 때문이다. Fig. 8(b)에서 |cos(βd)| > 1인 구간에 해당하는 주파수 범위가 stopband에 해당되며, Fig 8(b)에서 passband이외의 구간이 stopband에 해당된다.
Fig. 9는 식 (17)을 적용하여 passband 및 stopband의 kd와 βd를 한 개의 그래프에 모두 표시한 그림이다. 통과대역에서는 β값은 실수이므로, 그림에서 통과대역은 β값의 허수가 0에 해당되는 주파수 범위이다. 따라서, 그림에서 β값의 허수가 0이 되는 부분이 passband가 되며 이는 Fig. 8(b)에서|cos(βd)| < 1에 해당하는 주파수 범위와 동일하다.
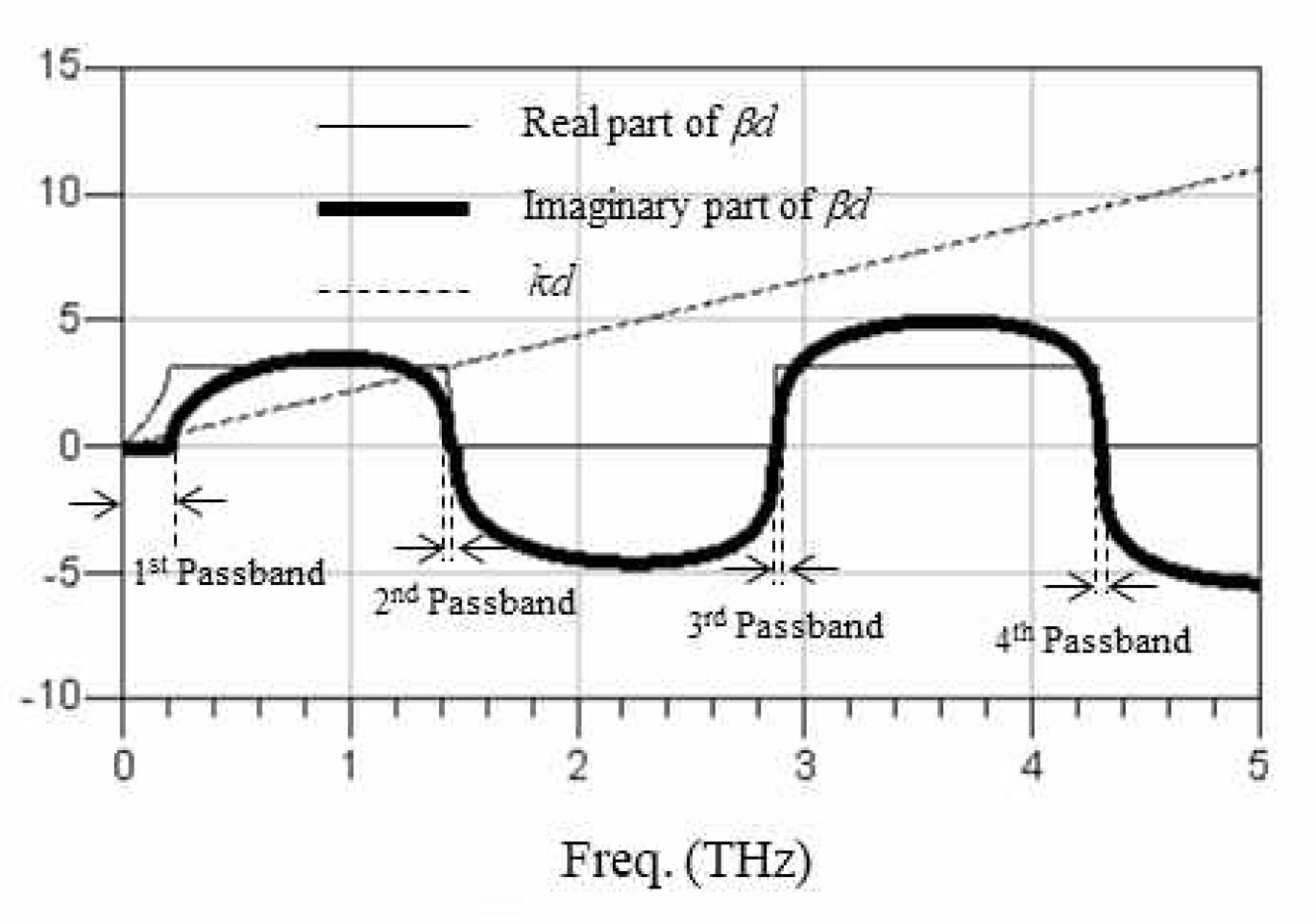
Fig. 9에서 β값의 허수가 0이 되는 부분이 passband에서 읽은 β값을 x축에 표시하고, 이에 해당하는 k값을 y축에 표기하면, Fig. 10과 같은 k-β 다이어그램을 얻을 수 있다.
k-β 다이어그램으로부터 추출한 다양한 LT값에 대한 passband 및 stopband 특성결과는 Table 2에 요약되어 있다. 실지 RF 대역에서 물리적으로 의미가 있는 대역폭은 1차 통과대역 (1st passband)이며, CWP3DCS 선로구조의 경우 주기적 구조의 길이 LT = 30 ∼ 150 μm의 범위에서 121.2 GHz까지는 전송선로로서 사용이 가능함을 알 수 있다. 그리고, 주기적 구조의 길이 LT가 감소할수록 1차 passband의 대역폭이 증가하는데, 그 이유는 LT가 감소할수록 주기적인 병렬용량 값이 감소하기 때문이다. 즉, CWP3DCS 선로구조는 주기적으로 인덕터와 커패시터가 연결된 저역필터로 생각할 수 있으며, 이러한 저역필터의 차단주파수는 다음의 식으로 표현된다.
식 (18)에서 Lt, Ct는 각각 Fig. 2(b)의 등가회로에서 보이는 주기적인 인덕턴스와 용량에 해당하며, Ct는 식 (2)로 표현된다. 상기 식에서 알 수 있는 바와 같이 Ct값이 감소하면 대역폭에 해당하는 차단주파수 fc값은 증가하게 된다. Fig. 2(a)에서 볼 수 있는 바와 같이 LT값이 감소할수록 T형 스터브의 길이가 짧아지므로 용량 Ct값은 감소하게 되며, 식 (18)로부터 LT값이 감소할수록 Ct값의 감소에 의해 차단주파수 fc이 증가함을 알 수 있다. 구체적으로 LT = 30 μm인 경우 CWP3DCS는 297 GHz의 대역폭을 가진다. Table 3은 CWP3DCS 선로구조의 용량 Ct값에 대한 LT의 존성을 보여주며, 주기적 구조의 길이 LT값이 증가할수록 용량 Ct값이 증가하는 것을 알 수 있다.
대역폭 특성연구로부터 CWP3DCS 선로구조의 경우 주기적구조의 길이 LT = 30 ∼ 150 μm의 범위에서 121.2 GHz까지는 전송선로로서 사용이 가능함을 알 수 있지만, 실지 RF용 전송선로의 성능을 고찰하기 위해서는 121.2 GHz에서의 손실부분도 고려해야 한다. 반도체상의 전송선로를 100 GHz이상까지 정확히 측정하는 것은 상당히 어려운 실정이다. 그 이유는 높은 주파수에서 측정 probe와 반도체 상의 측정 PAD 사이의 접촉부분에서 고주파 기생성분이 발생하여 전송선로의 손실 값보다 이러한 기생성분이 야기하는 손실이 더 크기 때문에, 오차없이 전송선로 자체만의 손실특성을 추출하는 것은 상당히 어렵다. 따라서, 이러한 주파수 대역의 해석은 측정보다는 FEM (Finite Element Method)등의 full wave 전자계 해석법 혹은 등가회로에 의한 손실저항 추출법 등을 이용한다 (Wu et al., 2019). 본 논문에서는 CWP3DCS 선로구조의 등가회로로부터 저항을 추출하는 방법을 이용하여 상기 주파수 근방에서의 손실을 고찰하였다. Fig. 11은 손실부분을 고려한 등가회로이다. 100 GHz 이상의 주파수에서 손실부분을 고려하기 위해서 Fig. 2(b)의 등가회로에 직렬저항 Rs와 병렬저항 Rp를 추가하였으며, Fig. 2(b)에서 병렬로 연결된 Ca, Cμ와 CS를 1개의 커패시터 Ct로 표현하였으며 식(2)에 의해 정의된다. 전송선로가 완전도체가 아닌 경우 컨덕턴스값은 유한한 값을 가지며, Rs는 유한한 값을 가지는 컨덕턴스에 의해 발생하는 손실이며, Rp는 전송선로로부터 접지까지의 누설전류로부터 발생되는 손실이다. Rp에 대해서 구체적으로 설명하면 다음과 같다. 실리콘 반도체의 경우 완전 절연체가 아니므로 전송선로로부터 접지까지의 미약한 누설전류가 존재하며 이를 반영하기 위한 저항이 Rp이다. 전송선로의 길이가 l인 경우 전송선로의 삽입손실 S21은 다음의 식으로 표현된다(Yun, 2018; Pozar, 1990).
식 (19)에서 α는 손실을 나타내는 attenuation constant 이며, Fig. 11과 같은 전송선로의 손실을 반영한 등가회로에서 α는 다음의 식으로 표현된다.
식 (20)에서 병렬저항 Rp는 무시할 수 있으며 상기 식은 다음과 같이 표현될 수 있다.
식 (21)과 같이 저항 Rp가 무시될 수 있는 이유는 다음과 같다. 실리콘기판의 경우 GaAs등의 화합물기판에 비해 비교적 큰 도전성을 보이며, 이로 인해 Fig. 11과 같이 실리콘기판을 경유하여 선로로부터 접지면으로 흐르는 전류가 발생하게 된다. Fig. 11의 등가회로에서는 저항성분 Rp를 통하여 흐르는 전류 IR이 실리콘기판을 경유하여 선로로부터 접지면으로 흐르는 전류이다. 그런데, Fig. 11에서 보는 바와 같이 등가회로 상에서 저항성분 Rp는 선로와 접지면 사이의 용량성분 Ct와 병렬로 연결되어 있다. 따라서, 선로와 접지면 사이의 용량성분 Ct는 저항성분 Rp와 병렬로 연결되어 Rp에 대해 bypass기능을 하게 된다. 이를 임피던스 측면으로 설명하면 다음과 같다. 100 GHz이상의 높은 주파수에서는 각주파수 ω가 상당히 커지므로 1/jωCt는 Rp에 비해 충분히 적은 값을 가지므로, 아래의 식과같이 Ct와 Rp로 이루어진 병렬회로의 임피던스 Zp에서 저항성분 Rp는 무시될 수 있다.
식 (22)로부터 주파수가 극도로 높아지면 저항성분 Rp를 무시할 수 있으므로 손실을 나타내는 attenuation constant α는 식 (21)로 나타낼 수 있다.
손실성분 α는 주파수가 증가할수록 식 (20)으로 표현되는 등가회로 식에 수렴하므로(Pozar, 1990), Rp가 무시될 수 있는 100 GHz이상의 주파수에서는 결국 α는 식 (21)에 수렴한다. 따라서, 본 논문에서는 S 파라메터 측정치로부터 Fig. 11의 등가회로에서 보여지는 Lt, Ct와 Rs를 추출하였으며, 추출된 값을 식 (19)와 (21)에 적용하여 삽입손실 S21을 등가회로로부터 추출하였다. 그 결과에 의하면 LT = 30 ∼ 150 μm의 범위에서 121.2 GHz에서 삽입손실 S21은 λ/4 길이를 가지는 CWP3DCS 선로구조에 대해 최대 1.6 dB의 손실특성을 보였다. 일반적으로 100 GHz이상에서는 트랜지스터 및 기타 RF 부품에서의 기생성분에 의한 높은 손실이 발생하나 트랜지스터의 이득을 증가시켜 손실부분을 보상하는 방법이 이용되며, 이를 고려하면 λ/4 길이를 가지는 CWP3DC에 대한 1.6 dB 손실특성은 121 GHz에서도 충분히 응용가능하다고 판단된다. 사실 현재의 밀리미터파 응용은 대부분 K/Ka밴드에 집중되어 있으므로 실지로는 100 GHz이상에서의 손실특성보다는 50 GHz정도까지의 손실특성이 더욱 중요하다. 이 범위에서의 CWP3DCS 선로구조에 대한 손실특성은 상당히 양호한 것으로 보고되어 있다 (Yun, 2018).
3.5 삽입손실 측정값으로부터 구한 Ct값을 반영한 특성 임피던스에 관한 measurement-based equation 유도
절차 5)에서 언급한 Ct 값을 반영한 특성임피던스에 관한 measurement-based equation의 유도과정은 다음과 같다. CWP3DCS 선로구조의 특성 임피던스를 계산하기 위하여 전압대 전류비로 정의하였을 경우 특성 임피던스의 식은 다음과 같다.
식 (23)을 식 (9) ~ (12)를 이용하여 풀이하면, 다음과 같다.
식 (24)에서 A=D라는 점을 이용하여 특성 임피던스 수식을 구하면 다음의 식과 같다.
식 (25)에서 b는 식 (8-2)로 표현되는 식이므로, 변수 값 b에 측정된 삽입손실 S21로부터 추출된 용량 값 Ct가 포함되어 있다. 식 (25)가 특성임피던스에 관한 measurement-based equation이 된다. Table 4는 측정된 특성 임피던스 값과 식 (25)로부터 추출된 특성임피던스 결과를 보여준다. 측정값은 각 전송선로에 대해 반사계수 측정치가 스미스차트에서 원점으로 수렴하는 지점의 임피던스 값을 추출한 결과이다. 특성임피던스는 약간의 주파수 분산특성을 보이므로 주파수에서 평균값을 취하였다. 비교결과에서 보는 바와 같이 측정값과 계산값이 잘 일치하는 것을 알 수 있으며, 최대오차는 3.9%이다.
Fig. 12는 특성 임피던스에 대한 measurement-based equation인 식 (25)로부터 추출한 CWP3DCS의 특성임피던스 결과이며, 주기적 구조의 길이 LT의 변화에 따른 주파수 의존성을 제시하였다. 그림에서 보는 바와 같이 주기적 구조의 길이 LT가 증가할수록 특성임피던스가 감소하는데, 이는 LT가 증가할수록 용량 Ct값이 커지기 때문이며 이에 대한 근거는 Table 3에 제시되어 있다. 즉, 주기적인 병렬커패시턴스의 단위 길이당 용량 Ct값은 식 (2)로 표현되며, 특성 임피던스는 단위 길이당 인덕턴스 값을 용량 값으로 나눈 값에 루트를 취한 값이므로(Pozar, 1990), Fig. 2(b)의 등가회로와 식 (2)로부터 임피던스는 다음 식으로 표현됨을 알 수 있다.
결국, Table 3의 결과와 식 (26)으로부터 LT가 증가할수록 Ct값이 증가하게 되고, 상기 식으로부터 CWP3DCS 선로구조의 특성임피던스 ZB값은 LT가 증가할수록 감소함을 직관적으로알 수 있다. 따라서, 주기적 구조의 길이 LT를 조절하면 CWP3DCS 선로구조의 특성임피던스 Z B값을 쉽게 조절할 수 있으며, 이러한 방법에 의해 다양한 특성임피던스 값을 가지는 CWP3DCS 선로구조를 쉽게 구현할 수 있다.
Fig. 12에서 알 수 있는 바와 같이 CWP3DCS 구조는0 ~ 50 GHz의 범위에서 주파수가 변화하더라도 임피던스의 변화는 매우 미미한 것을 알 수 있다. 구체적으로 LT = 30μm인 경우 특성임피던스는 19.0 ~ 19.2 Ω의 값을 가진다. 기존의 주기적 구조의 경우, 주파수 변화에 따른 특성 임피던스 변화가커서, 전송선로에는 응용되지 못하고 필터에 주로 이용되었다(Ahn et al., 2001; Gao et al., 2005). 그러나 CWP3DCS 구조의 경우 주파수 변화에 따른 특성 임피던스의 변화가 미미하므로 광대역의 전송선로 및 광대역 분포정수형 수동소자에 이용될 수 있음을 알 수 있다.
그리고, Fig. 12로부터 알 수 있는 CWP3DCS 구조의 중요한 장점은 선로의 길이 뿐 아니라 선포 폭이 크게 감소된다는 사실이다. 실리콘 기판 상에 제작된 종래의 전송선로를 이용하는 경우 10 GHz에서 파장이 10.2 mm이며, 20 Ω이하의 특성임피던스를 가지는 선로를 제작하기 위해서는 선로 폭이 3 mm이상이 되어야 한다 (Yun, 2017; Pozar, 1990). 그러나, Fig. 12에서 보는 바와 같이 CWP3DCS 구조를 사용하는 경우 20 μm의 선로 폭으로도 20 Ω이하의 낮은 임피던스를 가지는 전송선로의 구현이 가능하며, 기존 전송선로에 선로 폭 선로폭이 크게 감소하는 것을 알 수 있다.
4. 결 론
본 연구에서는 measurement-based equation을 이용하여 3D 결합구조를 가지는 코프레너 선로인 CWP3DCS 구조에 대한 특성 임피던스와 대역폭 특성을 연구하였으며 이를 통해 완전집적형 FISoC로서의 응용가능성을 검토하였다. 삽입손실에 대한 측정값을 반영한 measurement-based equation으로부터 추출된 특성임피던스와 전송상수 β는 각각 3.9%와 6.4%의 최대오차를 보여주었으며, 이로부터 measurement-based equation 유효성을 확인하였다.
본 논문의 결과에 의하면, CWP3DCS는 121 GHz까지 전송선로로써 사용이 가능함을 알 수 있었다. 구체적으로는 CWP3DCS는 주기적 구조의 길이 LT = 30 ∼ 150 μm의 범위에서 통과대역이 121 GHz인 대역폭 특성을 보여주었으며, LT = 30 μm인 경우 297 GHz의 광대역 특성을 보여주었다. 그리고, 주기적 구조의 길이 LT값이 감소할수록 통과대역의 대역폭이 증가하였으며, 이에 대한 이유는 LT값이 감소할수록 주기적인 용량 Ct값이 감소하여 차단주파수가 증가하기 때문이 었다.
그리고, CWP3DCS 구조를 사용함으로써 20 μm의 선로 폭으로도 20 Ω이하의 낮은 임피던스를 가지는 전송선로의 구현이 가능하였으며, 동일한 임피던스를 가지는 기존 전송선로의 선로 폭 3mm에 비해 선로 폭이 크게 감소하였다. 주기적 구조의 길이 LT값을 조정하면 CWP3DCS 구조의 특성임피던스 Z B값을 쉽게 조정할 수 있었으며, 이 결과로부터 원하는 특성임피던스 값을 가지는 구조를 반도체 기판 상에서 용이하게 구현할 수 있음을 알 수 있었다. 그리고 CWP3DCS 구조의 특성임피던스는 종래의 주기적 구조와는 달리 아주 적은 주파수 의존성을 나타내었으며, 이 결과로부터 CWP3DCS 구조는 광대역의 반도체 집적회로용 수동소자에 이용될 수 있음을 알 수 있었다.
상기 결과들로부터 CWP3DCS 구조는 무선통신소자용 정합 및 수동소자로써 유용하게 사용될 수 있음을 알 수 있다. 본 논문은 3D 결합구조를 가지는 코프레너 선로인 CWP3DCS의 대역폭에 대한 최초의 연구이다.






 PDF Links
PDF Links PubReader
PubReader ePub Link
ePub Link Full text via DOI
Full text via DOI Download Citation
Download Citation Print
Print