선박의 제어 입력과 속도 출력 학습에 의한 단순 운동학 모델 생성
Simple Kinematic Model Generation by Learning Control Inputs and Velocity Outputs of a Ship
Article information
Abstract
본 연구에서는 선박의 운항 데이터를 기반으로 조종성능을 모사할 수 있는 단순 운동학 모델을 제안하였다. 수평면 3자유도 각 방향의 속도 성분을 1차 미분방정식의 해 형태의 단순모델로 두고, 계수에 대한 운항데이터 학습을 수행하였다. 실제 선박의 충분한 운항 데이터의 확보는 어렵거나 제한적이므로, 본 연구에서는 실 운항 데이터 대신 공개된 동역학 모델을 활용하여 임의의 제어입력에 대한 시뮬레이션 결과를 얻고, 이를 운항데이터 학습에 활용하였다. 제어입력인 프로펠러 회전수 및 타각을 임의로 부가하여 동역학 시뮬레이션을 수행하고 각 속도 성분 출력을 얻었다. 충분한 시간 동안 동역학 시뮬레이션의 제어 입력과 속도 출력을 학습하여 각 제어 입력에 대한 운동학 모델 내 계수인 시정수 3개, 수렴속도성분 3개의 분포를 도출하였다. 추가로 임의의 제어 입력에 의한 선회 시뮬레이션 결과들과 비교함으로써 단순 운동학 모델의 성능을 검증하였다. 도출된 시정수들의 분포에는 다소 분산이 있으며, 제어 입력 이외의 관련 변수를 더 추가하여 정확도를 높이는 추후 연구가 필요하다.
Trans Abstract
A simple kinematic model for the prediction of ship manoeuvres based on trial data is proposed in this study. The model consists of first order differential equations in surge, sway, and yaw directions which simulate the time series of each velocity component. Actually instead of sea trial data, dynamic model simulations are conducted with randomly varied control inputs such as propeller revolution rates and rudder angles. Based on learning of control inputs and velocity outputs of dynamic model simulations in sufficient time, kinematic model coefficients are optimized so that the kinematic model can be approximately reproduce the velocity outputs of dynamic model simulations with arbitrary control inputs. The resultant kinematic model is verified with new dynamic simulation sets.
1. 서 론
선박이 목적지까지 안전하게 이동하려면 충분한 조종성능 확보가 필요하다. 대상 선박의 설계 단계에서 조종성능을 파악하기 위하여 일반적으로 모형실험, 수치계산 등 결과에 기반한 동역학 모델 시뮬레이션을 수행한다. 이러한 시뮬레이션 모델은 대상 선박의 건조 후 실제 운항 중에도 경로 예측 등에 참고 자료로 활용될 수 있다.
한편 최근 자율화, 무인화 선박들이 증가하면서 자선의 장애물 조우 시 회피 여부 판단, 주변 환경을 고려한 경로 자동 탐색 등을 위하여 시뮬레이션의 필요성이 증가되고 있다(Cho et al., 2021). 운항 선박의 실시간 조종성능을 정도 높게 예측할 수 있다면 충돌 회피 등의 기동을 자율화하는 데에도 큰 도움이 될 것이다. 그러나 실제로 정확한 동역학 모델이 준비되어 있는 선박은 매우 일부에 불과하다.
본 연구에서는 이와 같이 정밀한 동역학 모델이 마련되지 않은 선박을 대상으로 한다. 대상선의 충분한 기간 동안 운항 데이터를 확보할 수 있을 경우 이를 활용하여 조종성능을 근사적으로 모사할 수 있는 단순 운동학 모델을 제안하였다. 선박의 단순 모델에 대한 선행 연구를 보면 Nomoto et al. (1957)에 의하여 선회율을 미분 방정식의 해로 근사하는 KT 모델이 제안된 이후 다양한 연구에서 활용되었으며, Norrbin (1965), van Leeuwen(1970)에 의하여 KT 모델에 비선형 항 및 속도 변화 수식이 추가되었다. 이를 활용한 Lee and Lee (1998), Yoon et al. (2007), Kim et al. (2010) 등의 최근 연구들도 있다. 본 연구에서는 선행 연구들을 참고하여 수평면 3 자유도 속도 성분 이력을 각각 1차 미분방정식의 해 형태로 설정하였다. 그리고 운항 데이터의 제어 입력과 속도 출력 정보 학습을 통하여 운동학 모델 계수들의 분포를 취득하였다. 실선 운항 데이터 확보는 제한이 있으므로 본 연구 내에서는 운항 데이터 대신 동역학 시뮬레이션 결과를 사용하여 학습을 수행하였다. 학습 대상 데이터의 제어 입력 운용 범위가 제한적일 경우, 얻어지는 계수 분포 범위도 제한이 있다. 제어 입력의 전 범위 내에서 충분한 시간 학습을 수행하고 이에 기반한 운동학 모델을 생성한 후, 추가 시뮬레이션을 통하여 그 성능을 검증하였다.
2. 선박 동역학 시뮬레이션
본 연구는 실제 선박의 운항 데이터에 기반한 운동학 모델 생성을 최종 목적으로 한다. 다만 현실적으로 충분한 실선 운항 데이터 확보가 어렵거나 제한적이므로, 실제 선박 거동을 유사하게 재현하는 동역학 모델의 시뮬레이션 결과를 기반으로 하여 운동학 모델을 생성하였다.
2.1 대상 모형선 제원
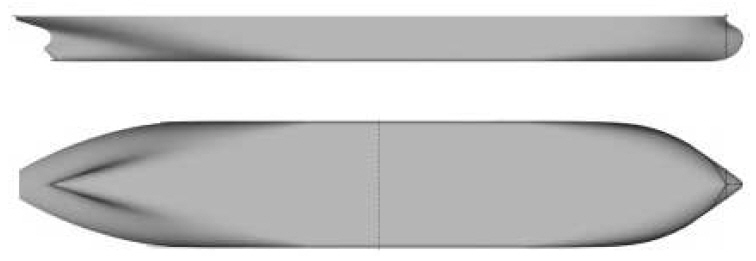
대상선은 공시선형인 KVLCC2 의 1/100 축소 모형선이다. KVLCC2는 모형실험, 시뮬레이션 등에 의한 운항 특성의 연구 사례들이 많으며, Kim et al. (2019, 2021) 등 연구에서 활용된 바 있다. 주요 제원 및 측면, 저면 형상은 각각 Table 1, Fig. 1과 같다.
Main particulars of a 1/100 scaled KVLCC2 model
Side and bottom views of KVLCC2 hul
2.2 동역학 모델 시뮬레이션 및 검증
Yasukawa and Yoshimura(2015) 연구를 참고하여 대상선의 동역학 시뮬레이션을 수행하였다. 수평면 3자유도 MMG 조종운동방정식은 식 (1)과 같다. m, Iz는 질량, yaw 질량관 성모멘트이고, mx, my, Jz는 각각 surge, sway, yaw 방향 부가질량 및 부가관성모멘트이다. 아래첨자 m은 선박 midship 기준의 물리량을 의미한다. xG는 midship 기준 선체 길이방향 무게중심 좌표이다. 우변은 외력 성분이며, 아래첨자 H, R, P는 각각 선체력, 타력, 추력 성분이다.
Yasukawa and Yoshimura(2015) 선행 연구에서 동일 선형 1/110 축소 모형선의 구속시험 기반 무차원 유체력 미계수를 공개하였고, 이를 사용하였다. 단, 본 대상선의 스케일을 고려하여 설계속도 15.5 knots에 대응하는 모형선 자항점은 17.5 RPS(revolutions per second)로 변경하였고, 타각속도는 실선 기준 2.34°/s 로 하였다. 이후 검증을 위하여 소개되는 1/100 축소 자유항주모형시험의 조건과 같다.
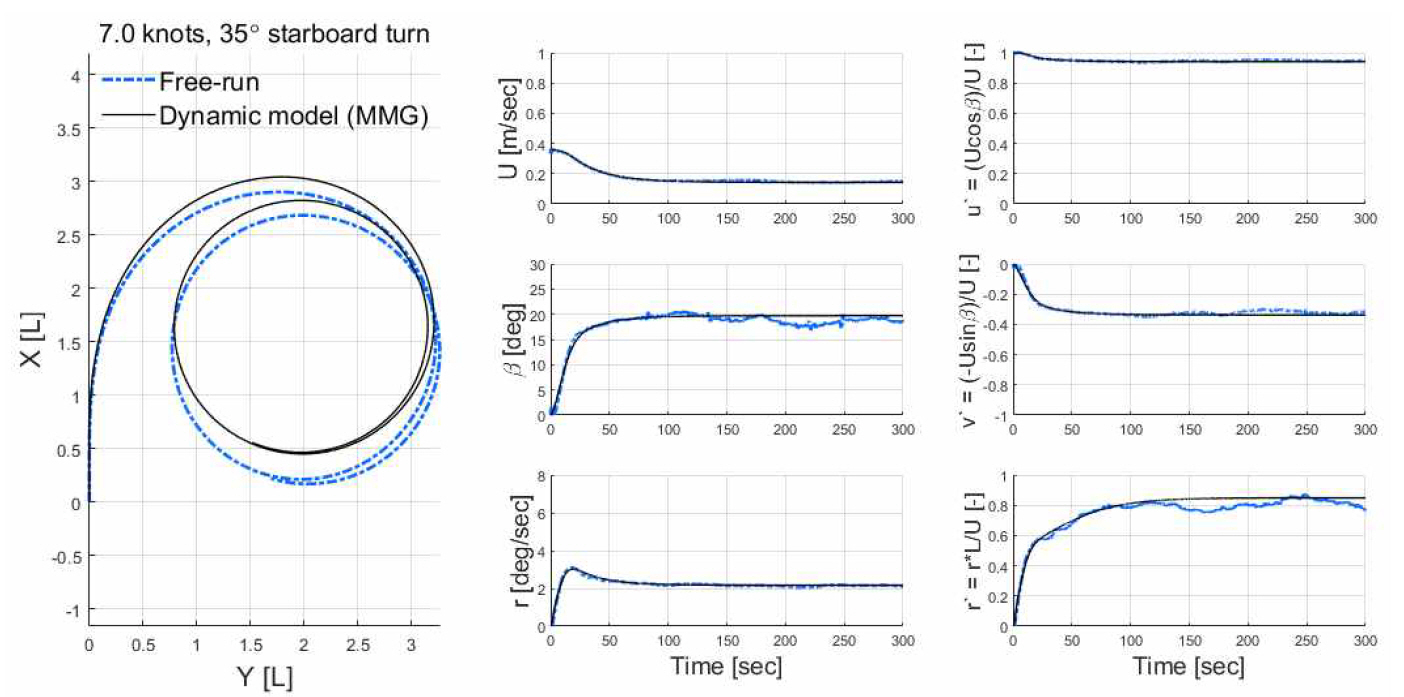
설계속도 15.5 knots에서 대표적인 35° 우현선회 시뮬레이션 결과와 선행 자유항주시험 간 비교는 Fig. 2와 같으며, 동역학 모델이 실제 모형선 속도 및 궤적을 유사하게 재현한다.
15.5 knots, 35° starboard turning circle test (Kim et al., 2019) & dynamic model simulation
운항속도가 크게 달라진다면 선박 주위 유동 특성이 바뀌므로, 엄밀하게는 설계속도 대상으로 추출한 유체력 미계수를 저속 영역에 그대로 적용 가능한지 재검토가 필요하다. 다만 본 연구에서는 동역학 모델이 넓은 선속 범위에서 물리적으로 큰 결점이 없는 정도로 가상의 운항 상태를 재현할 수 있다면 논리 전개 상 무리가 없다. 동일한 무차원 유체력 미계수를 사용하여 프로펠러 회전수 8.2 RPS, 초기속도 7.0 knots 에 대한 동역학 시뮬레이션을 수행하였다. 그 결과 Fig. 3처럼 자유항 주시험보다 선수각 90° 변경까지 전진방향으로 이동한 거리, 즉 전진거리(Advance)가 약간 크지만, 궤적과 속도 이력을 대체로 유사하게 재현함을 확인하였다.
7.0 knots, 35° starboard turning circle test (Kim et al., 2021) & dynamic model simulation
3. 단계적(stepwise) 입력에 대한 운동학 모델
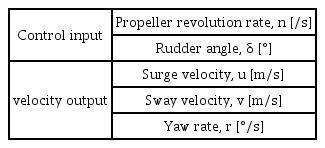
단순 운동학 모델 생성을 위한 선박의 제어 입력과 속도 출력 성분들을 정리하면 Table 2와 같다. 실제 선박 운항 중에는 제어 입력인 프로펠러 회전수와 타각이 시간에 따라 불규칙적으로 변화한다. 단, 두 입력 값이 고정된 후 일정한 시간이 흐른다면, 출력인 속도 성분들은 초반 천이 구간에서 증가, 혹은 감소하다가 일정한 값으로 수렴한다.
Ship control inputs and velocity outputs
본 연구 범위 내에서는 프로펠러 회전수와 타각이 특정 시점마다 단계적(stepwise)으로 변동하고, 각 변동 시점 간에는 속도 성분들이 수렴할 정도의 충분한 시간이 있음을 전제하기로 한다. 예를 들어 대상선이 6 RPS, 10° 입력 후 200초, 12 RPS, -5° 입력 후 150초, 12 RPS, 15° 입력 후 180초 운항하는 상황의 궤적 및 속도 시계열을 동역학 모델로 구현하면 Fig. 4에 실선으로 나타내었다.
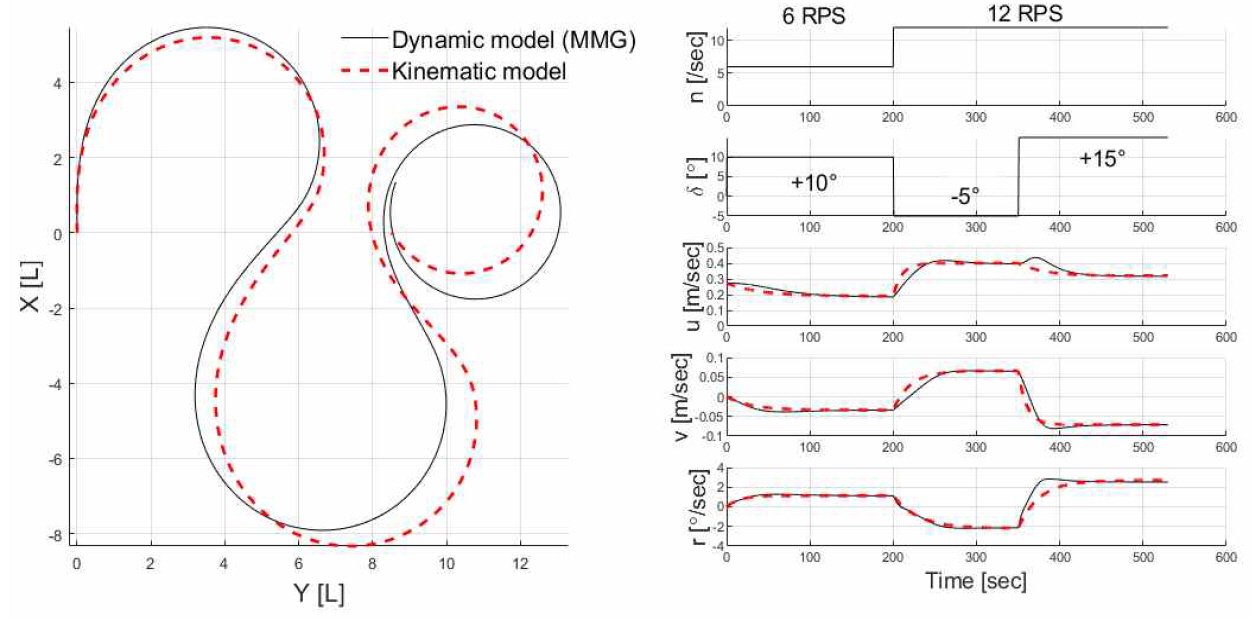
Dynamic simulation (solid) and simple kinematic model simulation (dotted) with stepwise control inputs
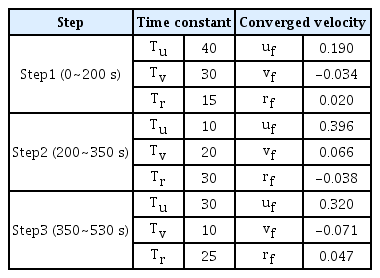
운동학적 관점에서 각 구간의 속도 성분 이력을 단순 모델링하면 식 (2)와 같이 1차 미분방정식 해 형태가 적절하다. Tu, Tv, Tr은 각 미분방정식 해의 증감 속도를 결정하는 시 정수이다. uf, vf, rf는 각 방정식 해들의 최종 수렴값이다. u, v와 r의 단위는 각각 m/s, rad/s 를 사용하였다.
식 (2)의 계수를 Fig. 4의 u, v, r 등의 상태변수 변화를 고려하여 Table 3과 같이 결정한 후 운동학 모델 시뮬레이션을 수행하고 Fig. 4에 점선으로 나타내었다. 동역학 모델로 재현한 궤적과 속도를 근사적으로 잘 표현함을 알 수 있다. 모델의 정확도를 높이려면 각 구간 별로 가장 적절한 계수 조합을 찾는 최적화 과정이 필요하다.
Coefficients in the kinematic model of Fig. 4
4. 임의의 운항 상황에 대한 운동학 모델 학습
4.1 운동학 모델 학습 전략
식 (1)의 동역학 모델로 임의의 운항 상황을 재현하고, 각 단계 별 Table 2의 입출력 정보를 학습함으로써 운동학 모델 계수를 다양한 입력 조건에 적용 가능하도록 일반화 할 수 있을 것이다. 최종 목적은 실제 선박의 임의의 운항 데이터의 학습이나, 본 연구에서는 동역학 시뮬레이션으로 대체한다.
식 (2)의 계수들 중 우변 수렴 속도 uf, vf, rf는 이전 선박 상태와는 무관하게 제어 입력을 고정한 후 충분한 시간이 지나면 유일하게 결정되는 값이다. 좌변의 시정수 Tu, Tv, Tr 는 천이 구간의 동특성에 관계되므로, 제어 입력뿐만 아니라 제어 입력 변경 직전의 선박 속도 및 가속도 등 상태변수에도 다소 영향을 받을 수 있다. 단, 본 연구는 운동학 모델의 실용성을 파악하는 초기 단계이므로, 시정수들도 제어 입력만의 함수로 한정하였다. 즉, 6개 계수는 모두 제어 입력 n과 δ만의 함수가 된다.
Fig. 5에 운동학 모델 계수의 구체적인 학습 절차를 나타내었다. 본 연구에서는 실제 선박 운항을 대체하는 동역학 모델에 단계(i=1∼m) 별 n, δ을 입력하면서 속도 u, v, r 전체 시계열을 출력한다. 각 단계에서 선수각 90°, 180° 변경까지 전진 및 횡방향으로 이동한 거리, 즉 전진거리(Advance) X090d, 전술직경(Tactical diameter) Y180d을 얻는다. 혹 해당 단계의 시간이 충분히 길지 않거나 타각이 매우 작다면 전진거리나 전술직경을 얻지 못할 수 있으며, 이 경우 해당 단계의 중간점 X좌표와 끝점 Y좌표를 각각 전진거리, 전술직경으로 대체하였다.
Flow diagram for learning of kinematic model coefficients
각 단계의 속도 시계열 출력 끝점 정보로부터 uf, vf, rf를 결정한다. 한편 각 단계에서 기 결정된 uf, vf, rf를 고정하고 시정수 Tu, Tv, Tr을 변경하면서 운동학 모델 시뮬레이션으로 전진거리 X090k, 전술직경 Y180k를 계산한다. 이들과 앞서 구한 X090d, Y180d 의 오차를 최소로 하는 Tu, Tv, Tr 최적 값을 도출한다. 이러한 과정 을 1∼m까지 모든 단계에 대하여 수행함으로써 제어 입력 n, δ에 대한 Tu, Tv, Tr, uf, vf, rf 분포 m개 세트를 얻는다.
4.2 Case 1 : 중고속, 소타각, 5시간, 입출력 100세트 학습
대상선의 설계속도 15.5 knots에 대응하는 모형선 프로펠러 회전수는 17.5 RPS이다. 즉, 대략적인 프로펠러 회전수 운용 범위는 0∼18 RPS, 타각 운용 범위는 우현 기동만으로 한정할 때 0∼35°이다.
실제 선박이 원양에서 운항하는 경우 원거리 전역 경로 경유점을 추종하는 중고속 전진 기동 위주이며, 급선회나 충돌회피 기동은 빈번하지 않으므로 타각을 대부분 작은 각도 범위에서만 사용하게 된다.
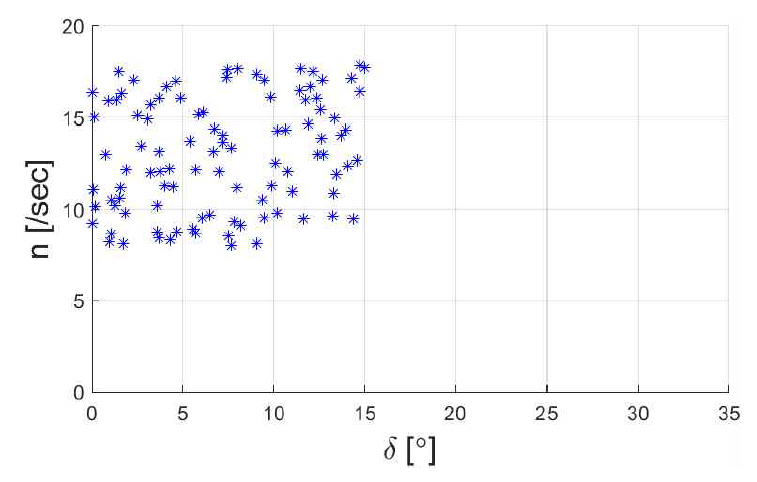
본 절에서는 Table 4와 같은 범위로 한정하여 모형선 기준 5시간, 총 100세트 입출력을 대상으로 운동학 모델 학습을 수행하였다. 프로펠러 회전수 상하한 8∼18 RPS는 각각 실선 기준 속도 약 7∼16 knots 에 대응한다.
Range of input variables in case 1
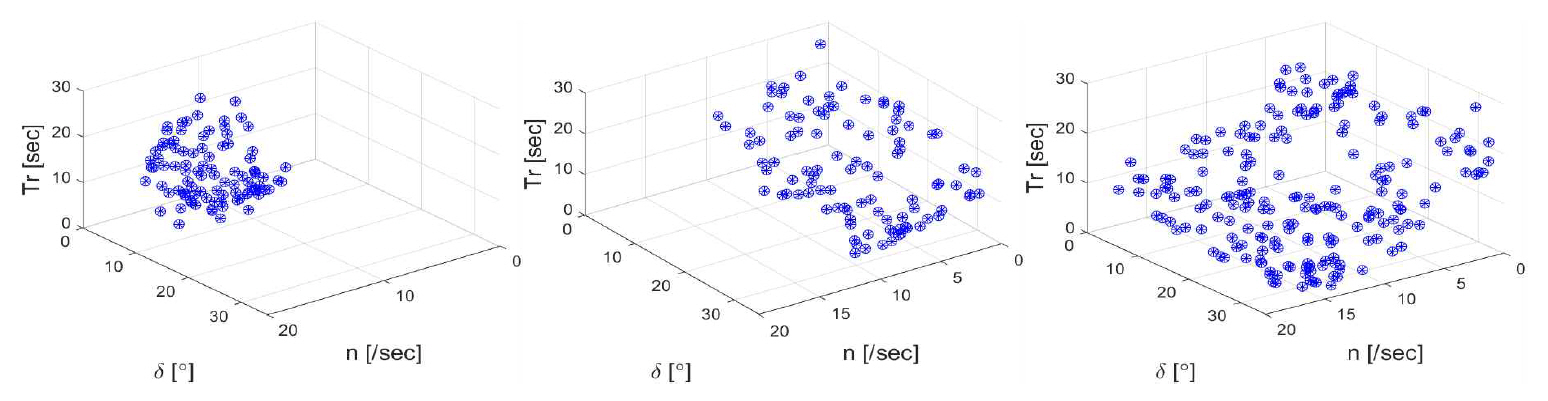
Table 4의 범위 내에서 각 단계 별 시간 및 제어 입력 n, δ는 랜덤함수를 통하여 배정하였고, Fig. 6에 가로축과 세로축을 각각 δ, n으로 하여 입력 값 분포를 나타내었다. 동역학 시뮬레이션으로 단계 별 계수를 최적화 후 운동학 시뮬레이션을 수행하고 둘을 단계별로 비교한 궤적, 입출력 시계열은 Appendix의 Fig. 17과 같다.
Distribution of input variables in case 1 (100 pt)
4.3 Case 2 : 저속, 대타각, 5시간, 입출력 100세트 학습
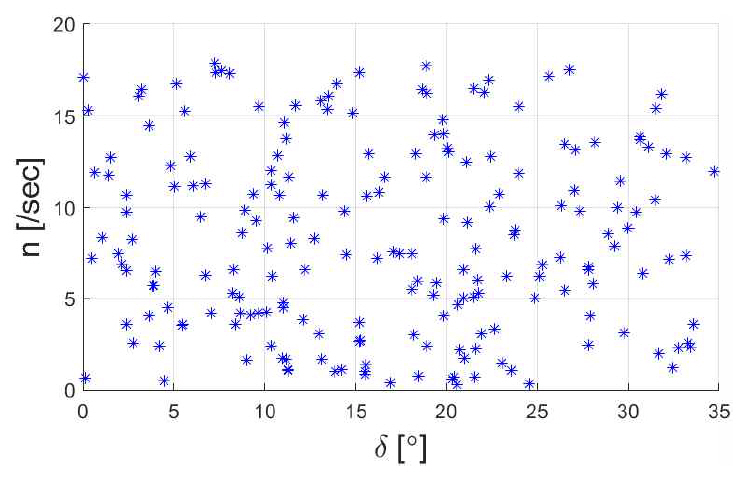
교통량이 많은 항내에서 선박이 운항하는 경우 대체로 선속이 낮으며, 묘박지 및 항구에 접안하거나 장애물 회피 등의 거동을 위하여 타각 운용 범위가 넓다. 이러한 상황을 모사하기 위하여 본 절에서는 Table 5와 같은 범위에서 제어 입력을 랜덤 배정하여 운동학 모델 학습을 수행하였다. 프로펠러 회전수 범위 0∼10 RPS는 실선 기준 속도 약 0∼9 knots 에 대응한다. 총 100세트의 제어 입력을 그래프로 나타내면 Fig. 7과 같다.
Range of input variables in case 2
Distribution of input variables in case 2 (100 pt)
앞 절과 같은 방법으로 동역학 시뮬레이션 결과를 사용하여 단계 별 최적화 된 계수로 운동학 시뮬레이션을 수행하고 궤적, 입출력 시계열을 비교하면 Appendix의 Fig. 18과 같다.
4.4 Case 3 : 전체 속도, 전체 타각, 10시간, 입출력 200세트 학습
앞의 중고속 소타각 조건, 저속 대타각 조건의 학습과의 결과 비교를 위하여 본 절에서는 전체 속도, 전체 타각 범위에서 학습을 수행하였다. 총 시뮬레이션 시간을 5시간에서 10시간으로 늘렸고, 입출력 세트 개수 역시 100세트에서 200세트로 증가시켰다. 구체적인 제어 입력 범위 및 랜덤 배정된 제어 입력 분포는 각각 Table 6, Fig. 8과 같다.
Range of input variables in case 3
Distribution of input variables in case 3 (200 pt)
동역학 시뮬레이션 입출력을 통하여 단계 별 계수 최적화 후 운동학 시뮬레이션을 수행하고 궤적, 입출력 시계열을 비교하면 Appendix의 Fig. 19와 같다.
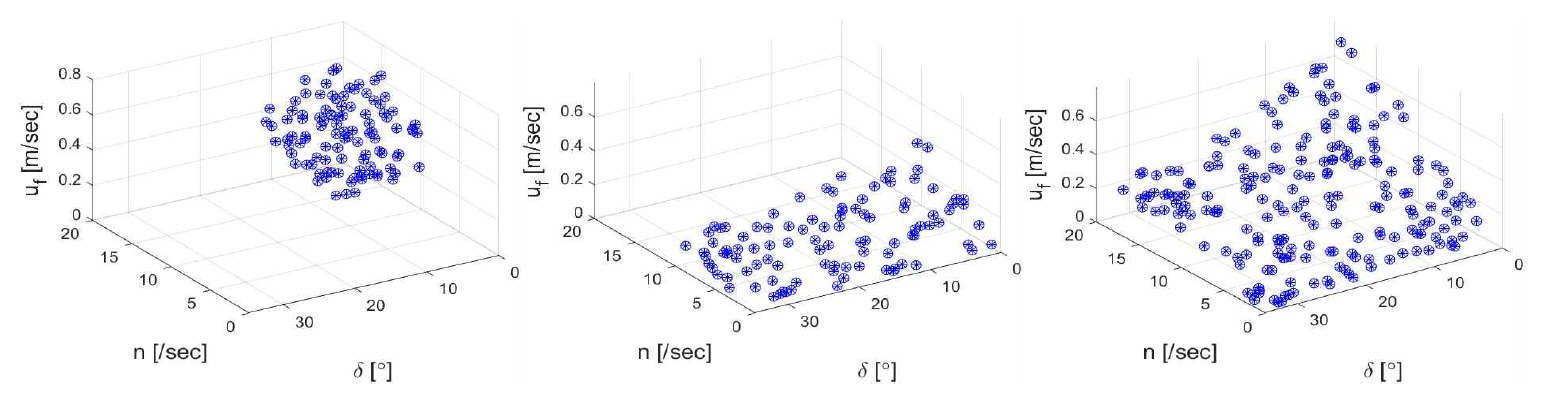
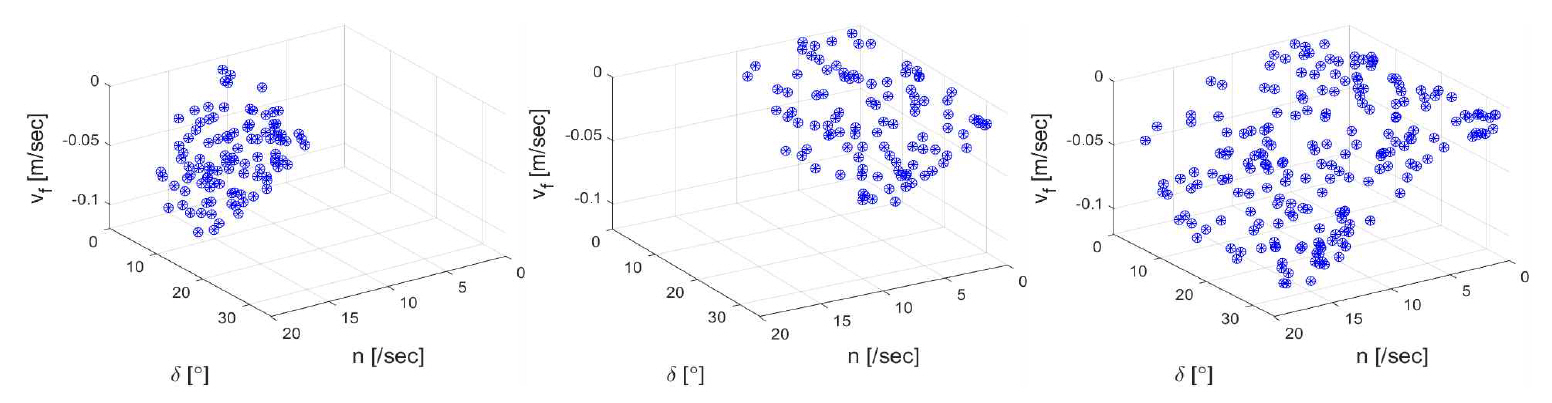
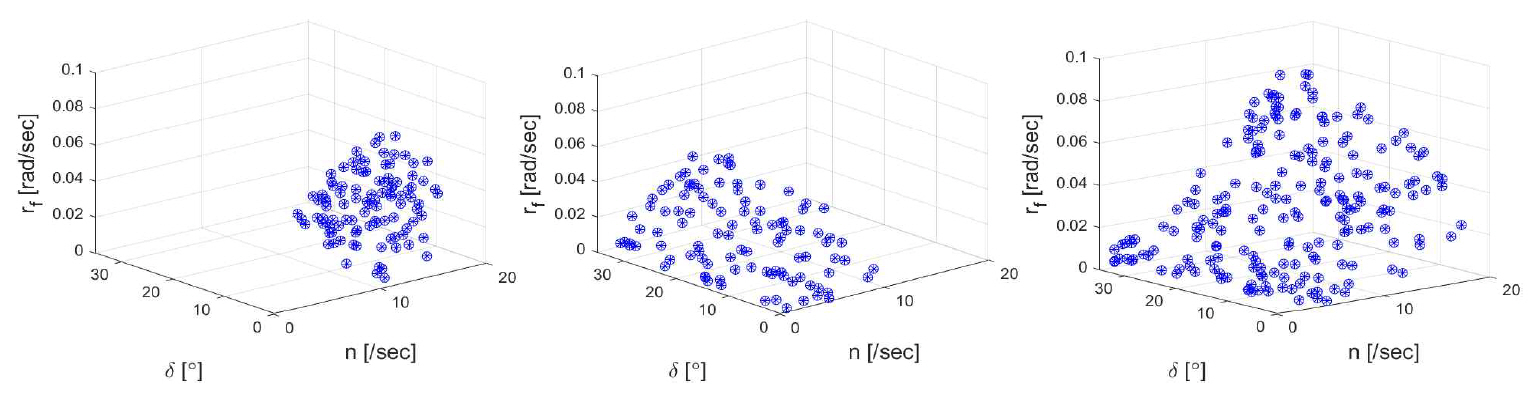
계수 uf, vf, rf, Tu, Tv, Tr의 Case 1, 2, 3 학습 결과를 Figs. 9∼14에서 비교하였다. 프로펠러 회전수가 높고 타각이 작을수록 전후속도 수렴 값 uf가 크다. 타각이 클수록 편류각이 커지므로 vf가 크며, 프로펠러 회전수가 높아서 합속도가 크면 타각이 작아도 vf의 크기는 상대적으로 크다. 프로펠러 회전수가 높고 타각이 크면 수렴 선회율 rf이 커진다.
Distributions of uf from Case 1 (left), Case 2 (middle), Case 3 (right)
Distributions of vf from Case 1 (left), Case 2 (middle), Case 3 (right)
Distributions of rf from Case 1 (left), Case 2 (middle), Case 3 (right)
Distributions of Tu from Case 1 (left), Case 2 (middle), Case 3 (right)
Distributions of Tv from Case 1 (left), Case 2 (middle), Case 3 (right)
Distributions of Tr from Case 1 (left), Case 2 (middle), Case 3 (right)
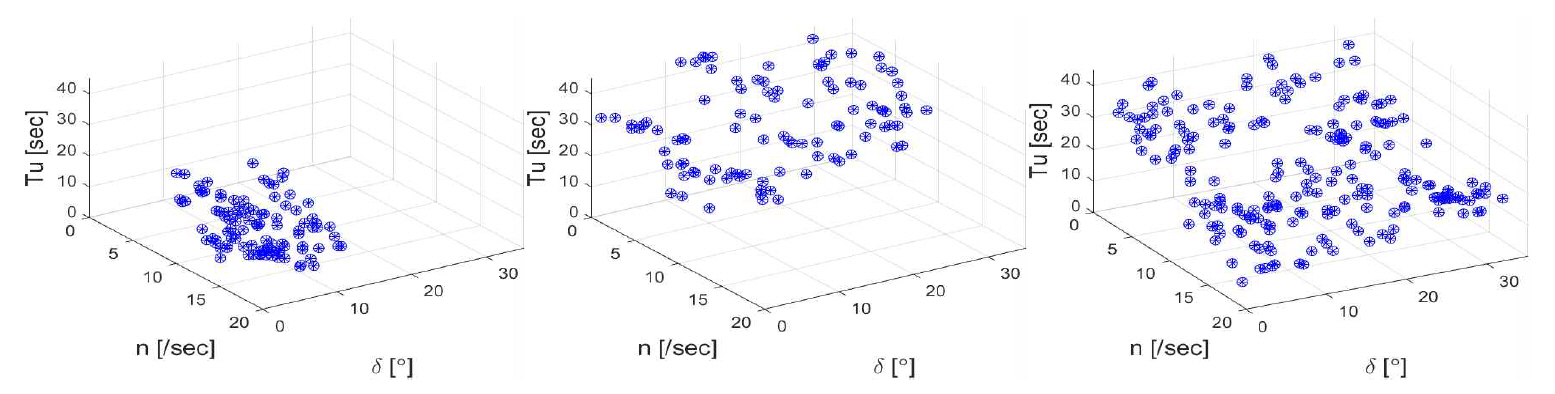
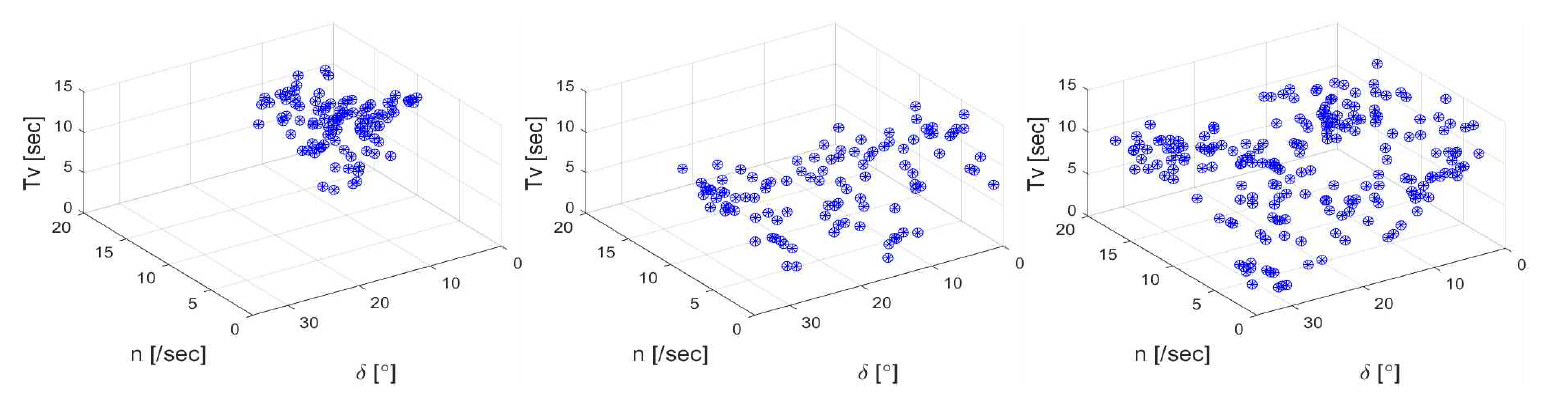
Figs. 12∼14에서 시정수 Tu, Tr은 프로펠러 회전수가 높을수록 작아진다. 즉, 추력이 크면 프로펠러 회전수에 대응하는 전후속도와 타각에 대응하는 선회율도 빠르게 수렴한다. 시정수 Tv는 프로펠러 회전수, 타각에 대한 경향이 명확하지 않으며 분산도 가장 크다. 계수들을 결정하는 기준으로 각 단계의 전진거리, 전술직경만을 활용하였고, Tv는 이와 같은 전체 궤적 변화에는 큰 영향을 주지 않는 것으로 추정된다.
Figs. 9∼14에서 일부 제어 입력 범위만을 다룬 Case 1과 Case 2의 계수 분포를 합하면 전체 제어 범위를 포괄하는 Case 3의 분포와 유사해진다. 제어 입력 n, δ에 대하여 계수들의 분포는 대체로 완만한 곡면 형태이다. 제어 입력에 대하여 평면 분포, 즉 완전한 선형성은 갖고 있지 않으므로 예를 들어 대양에서의 운항 데이터인 Case 1만 확보할 경우 항내의 저속 대타각 위주인 Case 2 운항 상태를 정확도 높게 추정하기는 한계가 있을 것으로 판단된다.
Case 1과 Case 2, 즉 원양과 항만 내에서 각각 충분한 운항 데이터를 확보한다면 둘을 합쳐서 Case 3에 가까운, 즉 전 제어 입력 범위에 가까운 계수 분포를 파악할 수 있으며, 이를 기반으로 한 운동학 모델을 활용하여 다양한 운항 상황을 추정할 수 있을 것이다.
5. 운동학 모델 성능 검증
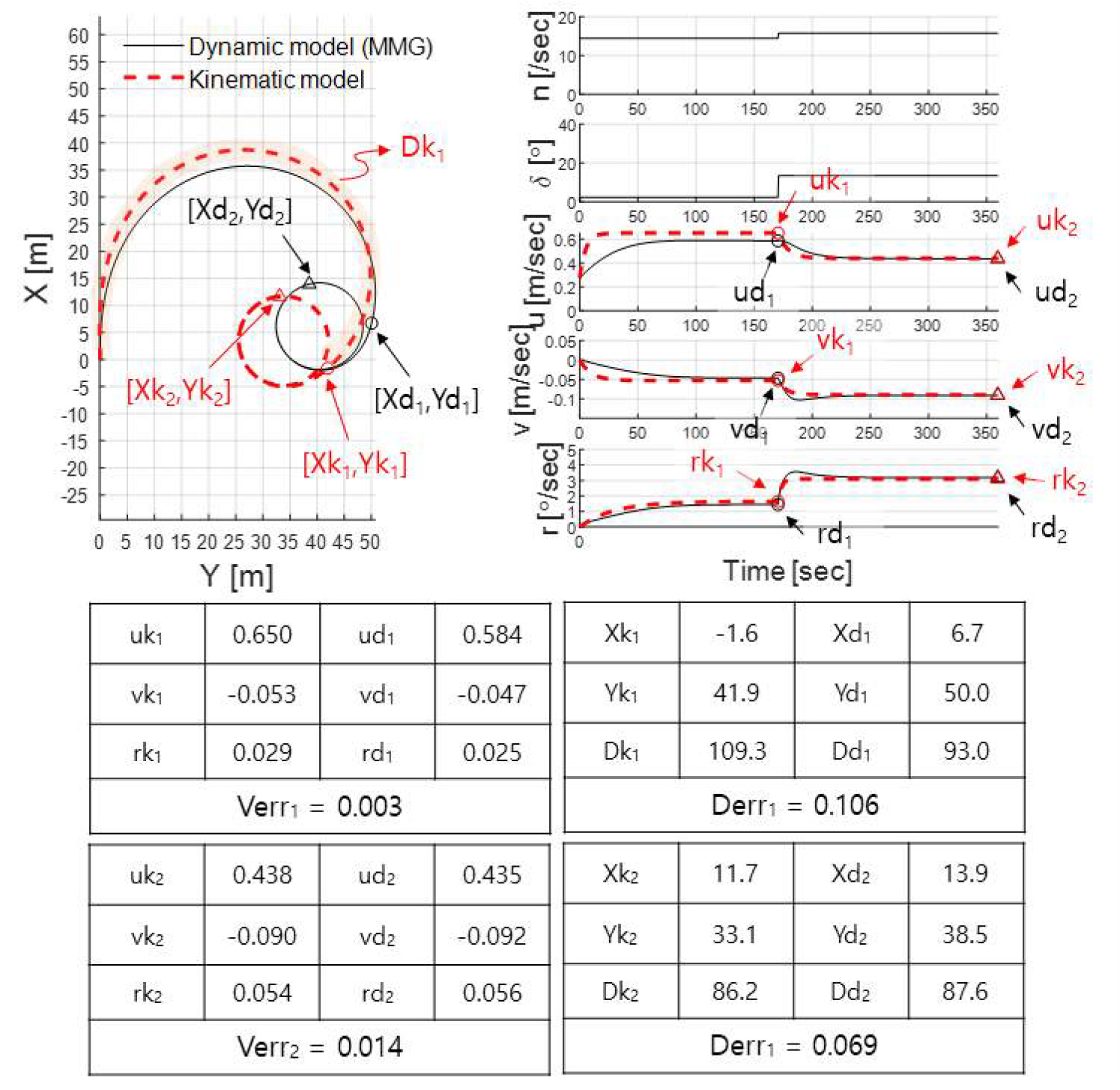
앞 장에서 학습된 계수 기반 운동학 모델의 검증을 위하여 제어 입력을 임의로 2회씩 변경하는 총 9회의 동역학 시뮬레이션과 비교하였다. 대표적인 검증 예를 Fig. 15 에 나타내었다. 각 그래프에서 붉은 점선은 매 단계의 제어 입력 정보만 주어진 상황에서 앞 장의 Case 3 학습으로 얻은 Figs. 9∼14 오른쪽 열 분포로 운동학 모델 계수를 추정한 후 시뮬레이션을 수행한 것이다. Figs. 9∼14에서와 같이 실제 계수 분포에는 분산이 존재하므로, 분포 데이터베이스 내에서 해당 제어 입력과 가장 가까운 점 3개의 평균을 사용하였다.
Verification (V01) of proposed kinematic model with coefficients learned in Case 3
검증 결과를 정량적으로 분석하기 위하여 Table 7과 같은 지수를 도입하였다. i는 단계 번호 1, 2이다. 아래첨자 k, d는 각각 운동학 모델, 동역학 모델 시뮬레이션 값을 뜻한다. 속도 성분의 무차원화는 식 (3)과 같다. L은 선박의 길이이다.
Converged velocity and distance error indices
지수 Verr는 각 단계 끝 점에서의 수렴 속도 성분들의 오차이며, 운동학 모델에서 uf, vf, rf 가 잘 추정되고 있는지 판단하는 기준이다. 한편 제어 입력 초반 천이 구간에서 Tu, Tv, Tr에 따른 속도 변화는 최종 궤적 오차에도 민감하게 영향을 준다. 이를 각 단계 최종 지점 위치 오차인 지수 Derr로 표현하였다.
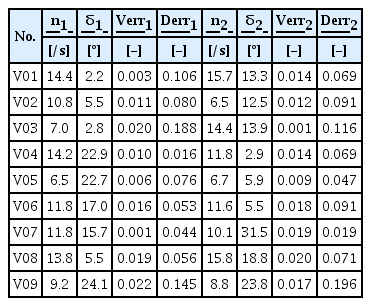
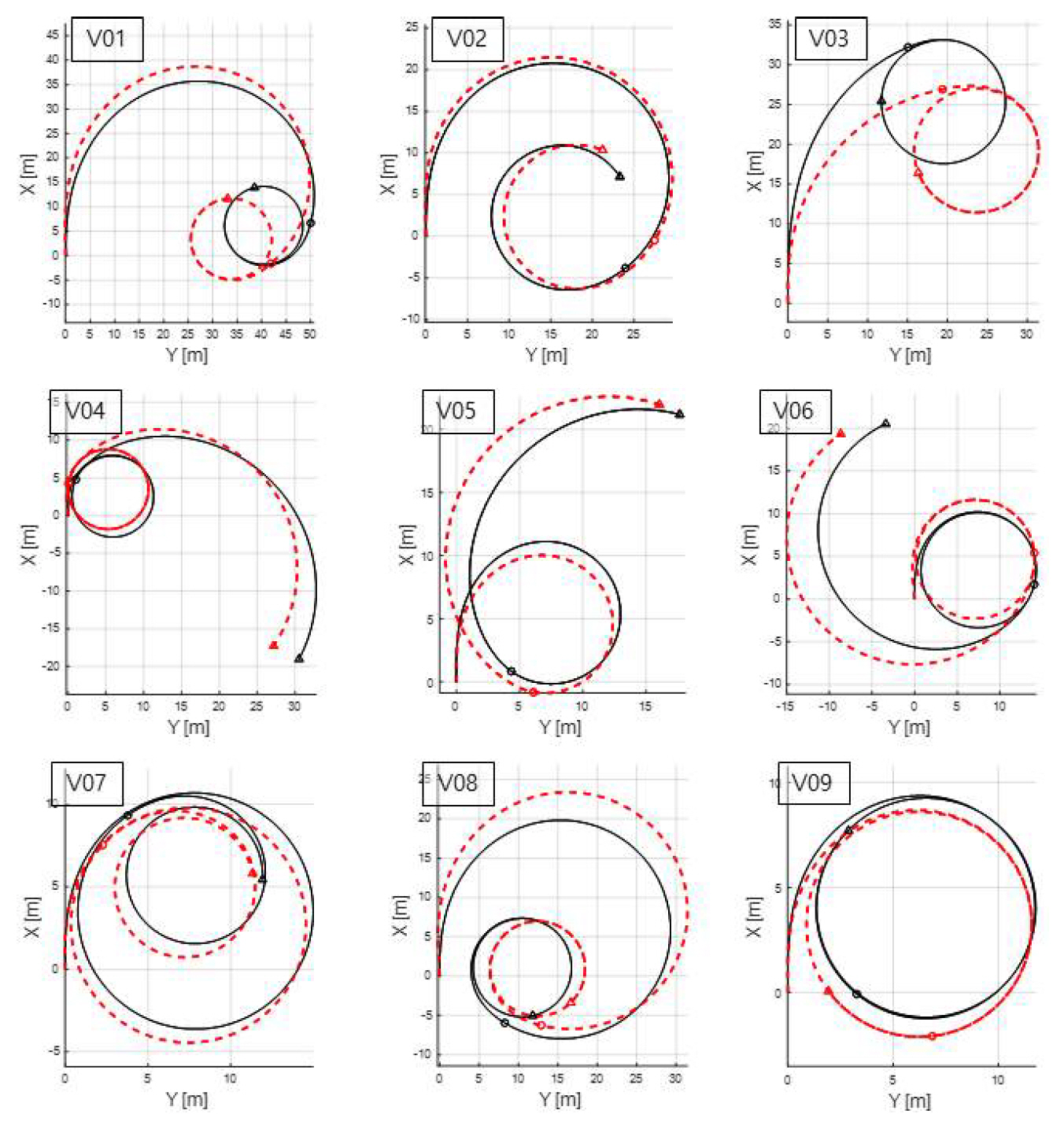
총 9가지 검증 시뮬레이션의 추출 지수들과 해당 궤적을 Table 8과 Fig. 16에 나타내었다. V03, V09의 Verr1이 1단계 다른 케이스에 비하여 높다. 작은 n, 즉 저속에서 수렴속도의 오차가 다소 증가할 수 있다. 하지만 V05와 같이 n이 작더라도 δ가 클 때, 수렴속도 오차가 작아지는 예외도 있다. 저속의 넓은 δ 범위에서 더욱 충분한 학습을 수행한다면 수렴속도의 오차를 줄일 수 있을 것으로 예상된다.
Velocity and position errors on verification sets
Trajectories of kinematic(dotted) and dynamic(solid) model in verification sets (V01 ∼ V09)
V03과 같이 특히 저속에서 δ가 작으면 Derr1이 비교적 크다. 이는 Fig. 19 궤적에서도 직관적으로 확인할 수 있다. 즉, 타각이 작아서 궤적이 선회보다 직진에 가까우면 속도 추정에 작은 오차가 있더라도 일정 시간 후 궤적의 오차가 상당히 축적된다. 최종 위치의 오차 감소에 초점을 둔다면, 작은 δ 범위에서 더욱 충분한 학습이 필요할 것이다.
대체로 수렴속도 추정 정확도는 높은 편이고, 각 단계의 선회직경 크기만 보면 동역학 시뮬레이션을 잘 재현하고 있다. 최종 위치의 오차는 대체로 시정수 Tu, Tv, Tr의 불확실성 때문으로 판단된다. Figs. 12∼14처럼 제어 입력 n, δ에 대한 시정수 분포의 분산들이 상대적으로 크기 때문이다. 근본적으로 시정수가 제어 입력 이외에도 입력 시작 순간의 선박 가속도, 속도 등 추가적인 변수의 영향을 받으리라 예상되며, 이에 대하여 추후에 더욱 정밀한 연구가 필요하다.
6. 결 론
본 연구에서는 선박의 단계적 프로펠러 회전수 및 타각 입력에 대한 수평면 속도 성분들의 이력을 각각 1차 미분방정식의 해로 근사하는 단순 운동학 모델을 제안하였다. 대상 선박의 임의의 프로펠러 회전수, 타각 입력에 대한 동역학 시뮬레이션 속도 성분 이력을 출력하고 이를 학습함으로써 제어 입력에 대한 운동학 모델 계수들의 분포를 취득하였다. 전체 프로펠러 회전수 및 타각 입력 범위에서 최대 200세트의 학습이 이루어졌고, 총 9가지의 사례를 통하여 제안된 운동학 모델의 정확도를 검증하였다. 구체적으로 각 단계 수렴속도, 최종 궤적 오차를 각각 지수화하고, 이를 통하여 모델의 정확도를 정량적으로 분석하였다. 운동학 모델로 재현한 궤적이 동역학 시뮬레이션과 더욱 일치하려면 특히 저속 영역 및 타각이 작은 조건에 대하여 충분한 케이스의 학습이 필요함을 확인하였다. 이러한 방법은 향후 실제 선박의 운항 데이터 학습으로 확장이 가능할 것이다. 다만 운동학 모델에서 천이 구간 변화에 관계된 시정수들은 제어 입력만으로 표현하는 데에 다소 한계가 있는 것으로 판단되며, 이에 대한 추가 연구가 필요하다.
Acknowledgements
본 연구는 선박해양플랜트연구소의 주요사업 “첨단운송체의 항내 운항성능향상을 위한 축척효과를 고려한 운항제어원천기술 개발(3/5)” (PES3860)의 연구 결과 중 일부입니다.
References
Appendix
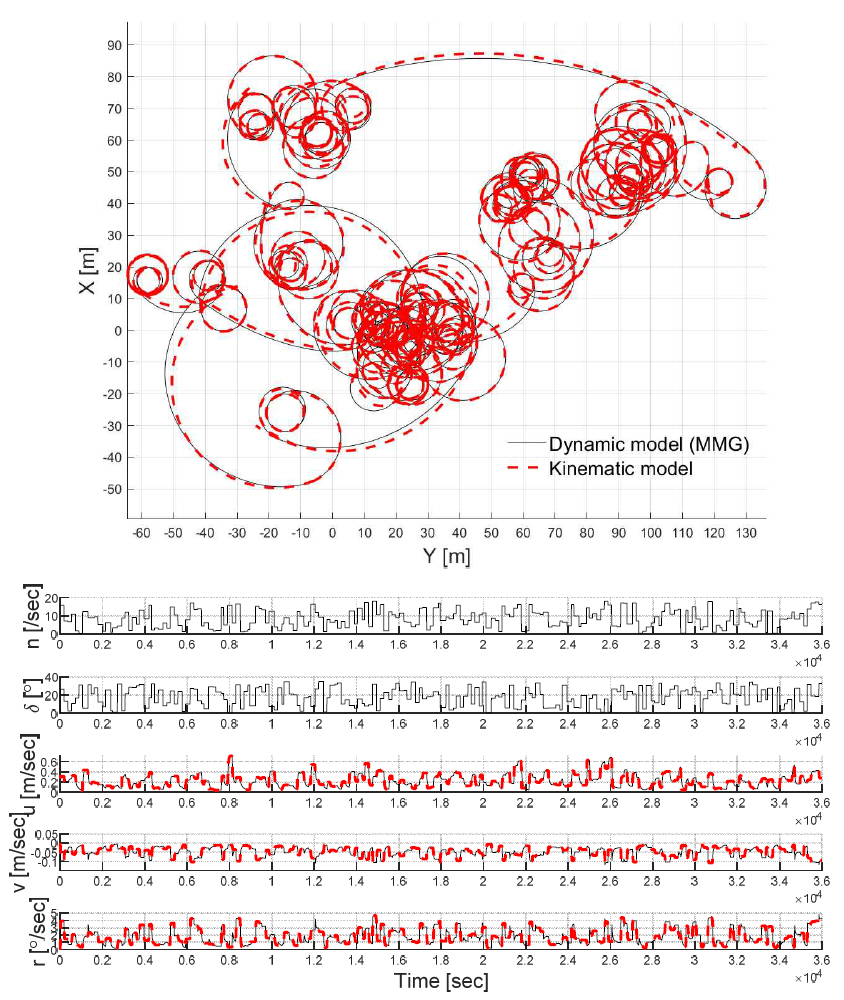
Appendix 1. Fig. 17 Trajectories, control inputs, and velocity outputs of kinematic model simulations with coefficients by learning dynamic simulations – Case 1 (high speed, small rudder angle)
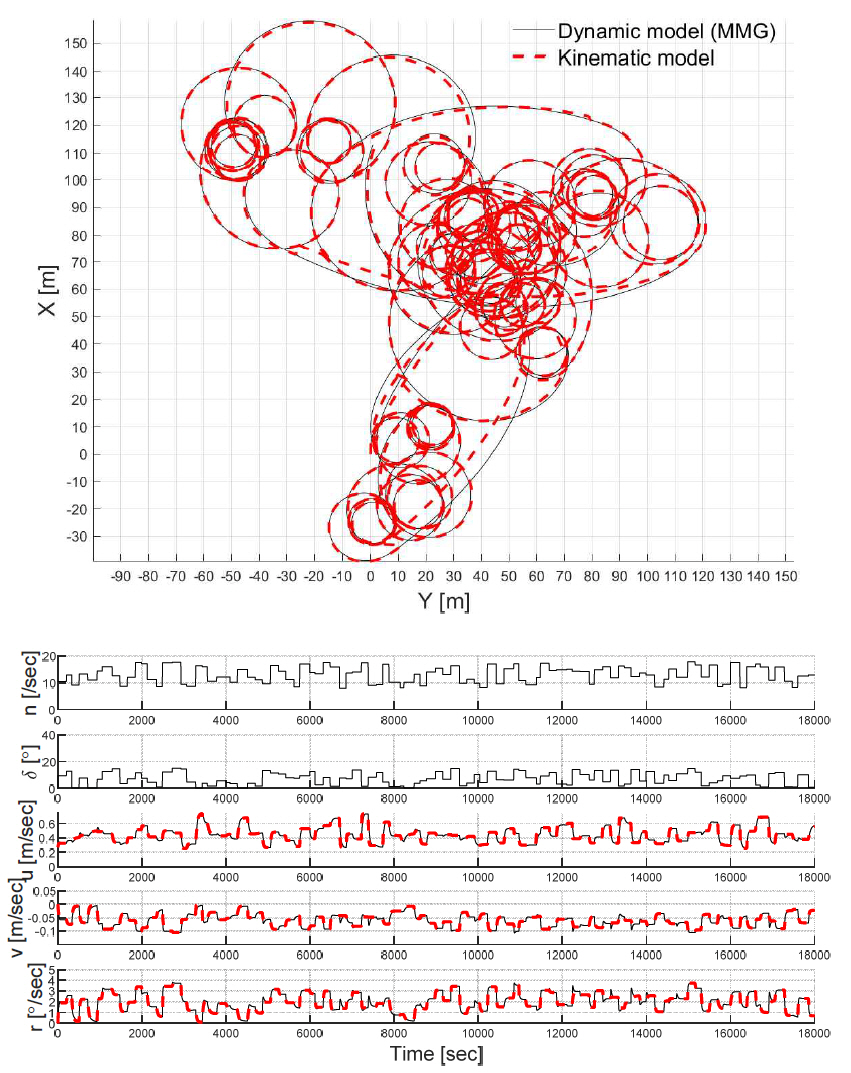
Appendix 2. Fig. 18 Trajectories, control inputs, and velocity outputs of kinematic model simulations with coefficients by learning dynamic simulations – Case 2 (low speed, large rudder angle)
Appendix 3. Fig. 19 Trajectories, control inputs, and velocity outputs of kinematic model simulations with coefficients by learning dynamic simulations – Case
