A Study on Sensitivity Analysis of the Hydrodynamic Derivatives on the Maneuverability Prediction of KVLCC2 in Shallow Water by Model Test
Article information
Abstract
In recent years, there have been concerted efforts toward predicting ship maneuvering in shallow water since the majority of ship’s accidents near harbors commonly occur in shallow and restricted waters. Enhancement of ship maneuverability at the design stage is crucial in ensuring that a ship navigates safely. However, though challenging, establishing the mathematical model of ship maneuvering motion is recognized as crucial toward accurately predicting the assessment of maneuverability. This paper focused on a study on sensitivity analysis of the hydrodynamic coefficients on the maneuverability prediction of KVLCC2 in shallow waters. Hydrodynamic coefficients at different water depths were estimated from the experimental results conducted in the square tank at Changwon National University (CWNU). The simulation of standard maneuvering of KVLLC2 in shallow waters was compared with the results of the Free Running Model Test (FRMT) in shallow waters from other institutes. Additionally the sensitivity analysis of all hydrodynamic coefficients was conducted by deviating each hydrodynamic derivative from the experimental results. The standard maneuvering parameters including turning tests and zig-zag maneuvers were conducted at different water depths and their effects on the standard maneuvering parameters were assessed to understand the importance of different derivatives in ship maneuvering in shallow waters.
1. Introduction
In recent years, intensive efforts have been focused toward the assessment of the maneuverability of a ship in shallow and confined water since most ship accidents near the harbor commonly occurs in these conditions. To ensure the safe navigation of a ship, the enhancement of ship maneuverability in the design phase is crucial. The determination of the hydrodynamic derivatives in the maneuvering equation of motion is important for predicting the ships’ trajectory at various water depths. Experimental method, theoretical method, and numerical method can be utilized to estimate the hydrodynamic derivatives in the equation of motion. However, a challenging area in the field of establishing the mathematical model of ship maneuvering motion is recognized as being important to accurately predict the assessment of maneuverability in a shallow water. Through sensitivity analysis of the hydrodynamic derivatives, the derivatives with the most significant impact can be. Numerous researchers have investigated the sensitivity analysis of hydrodynamic coefficient on the maneuvering prediction of a ship. Rhee and Kim(1999) estimated the hydrodynamic derivatives using a new trial method. They established that the sensitivities of linear and non-linear derivatives are greater and have a larger contribution in the zig-zag test. Kim et al.(2017) researched on the sensitivity analysis of hydrodynamic derivatives on the maneuverability of a tanker in shallow water. Their simulation was not compared with the Free Running Model Test(FRMT) in shallow water. In addition, the sensitivity analysis of non-linear derivatives which have a larger contribution in the prediction of ship maneuvering in shallow water was not conducted. Shenoi et al.(2016) conducted a sensitivity analysis of hydrodynamic derivatives on a container ship through numerical simulation using RANS solver. Wang et al.(2015) researched on the sensitivity analysis of hydrodynamic coefficients in 4 degrees of freedom ship maneuvering and simplified the mathematical model based on the sensitivity analysis results. Jeon et al.(2017) study based on the sensitivity analysis to develop the hull form of an underwater vehicle which satisfied the required intercept time of mission competence. Sen(2000) study was based on the sensitivity of maneuverability performance on the hydrodynamic derivatives of submerged bodies. He suggested that the linear damping coefficients have significant effects on the submarine’s trajectories. Generally, the majority of these studies involve the assessment of ship maneuvering in deep water through sensitivity analysis. All of the above-mentioned approaches have some limitations because the ship in deep water can be represented by linear as well as a simple nonlinear maneuvering model. However, when the ship moves in shallow waters, nonlinear effects gain prominence and a complete nonlinear model is necessary to establish the mathematical model of ship in shallow water. Through sensitivity analysis of hydrodynamic derivatives of ship in shallow water, the derivatives with the most significant impact can be found. In addition, a big challenge to test in shallow water is also the accuracy of tank bottom. This is the motivation to carry our the presented research. The objective of this study is to investigate on sensitivity analysis of the hydrodynamic derivative on the maneuverability prediction of KVLCC2 in shallow water. The hydrodynamic coefficients at various water depths are obtained from experimental results performed in the square tank of Changwon National University(CWNU) while the sensitivity analysis of all hydrodynamic coefficient is conducted by deviating each derivative hydrodynamic derivative from the experimental results. The standard maneuvering parameters of KVLCC2 in shallow water such as turning circle and zig-zag maneuvers are conducted at varying water depth and their effects on the standard maneuvering parameters are estimated to further comprehend the importance of different derivatives in ship maneuvering in shallow water.
2. Test facilities and test conditions
2.1 Test facilities
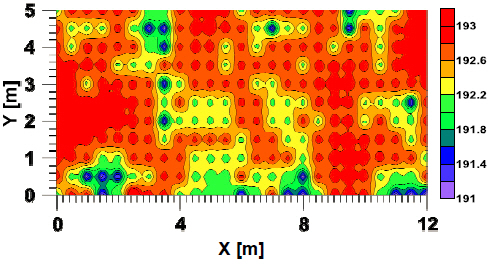
The model test was conducted in the square tank in CWNU as shown in Fig. 1. For the shallow water test, one of a big challenge is accuracy of the tank bottom. ITTC(2014) recommendation is that the vertical variation of the tank bottom be less than 10 % of the Under Keel Clearance(UKC). For this experiment, the precise tank bottom was built in January, 2018 with a precision of ±1 mm for ensuring the accuracy of tank bottom as shown in Fig. 2.
2.2 Test condition
The experiment was conducted in the square wave tank in CWNU, Korea. The KVLCC2 which was designed in Korea by the KRISO (Korea Research Institute of Ships and Ocean Engineering) was selected. The ship model used in this experiment has a scale factor of λ = 223. The principal particulars of the real and scaled model are listed as in Table 1.
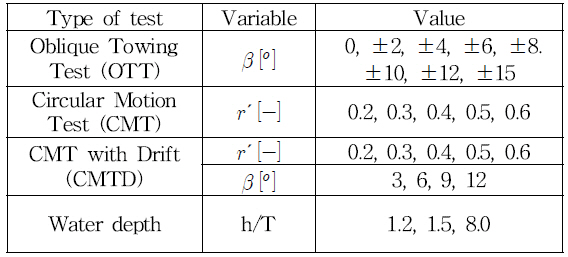
The model test was conducted at condition of a ship model and the ship speed was set at 0.241 m/s (equivalent to 7 knots in full scale). In addition, the principal particulars of the model ship by KRISO used to perform the Free Running Model Test (FRMT) is listed as in Table 1. The experiment was performed at varying water depths to obtain the hydrodynamic coefficients of KVLCC2 at various water depths. Test condition for obtaining the hydrodynamic coefficients are listed in Table 2.
3. Mathematical model and sensitivity analysis
3.1 Coordinate system
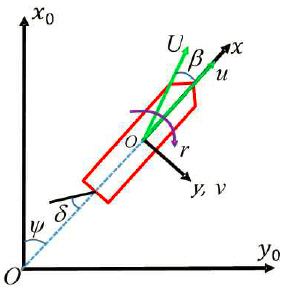
Mathematical model for maneuvering motion in 3DOF can be described as in Eq. (1). Two right-handed coordinate systems are adopted i.e. an earth-fixed coordinate system Ox0y0 and a body-fixed coordinated system Oxy as shown in Fig. 3.
3.2 Equation of motion
In order to predict the ships’ maneuverability, two types of hydrodynamic models are commonly used i.e. Abkowitz model and MMG (Maneuvering Modeling Group) model. In this experiment, MMG model for maneuvering motion in 3DOF was applied and it could be described as in Eq. (1). m is the mass of ship and Izz is the moment of inertia of ship in yaw motion. xG is the longitudinal position of ship’s gravity center. u and υ are the component of the velocity in the x-axis and y-axis direction, respectively.
3.3 Hull forces
Hydrodynamic forces and moments acting on a ship hull can be estimated using Eq. (3). mx, my and Jzz are the added mass of x axis direction, y axis direction, and added moment of inertia, respectively. Prime (′) inserted to the symbol refers to non-dimensional value. Non-dimensional of added mass and added moment of inertia can be estimated using Eq. (4). Non-dimensional sway velocity υ′, non-dimensional yaw rate r′ and resultant velocity U can be estimated using Eq. (5).
3.4 Propeller forces
The longitudinal force of the propeller of the propeller XP can be estimated using Eq. (6). tP, ρ and DP are the thrust deduction factor, water density, and the diameter of propeller, respectively. Thurst deduction factor tP is assumed to be constant at given propeller load for simplicity. KT is the thurst coefficient and can be expressed as a 3rd polynomial of propeller advance ratio JP using Eq. (7), k0, k1, k2, and k3 are coefficients representing KT .
3.5 Rudder forces
Rudder force and moment can be estimated through the combination of interaction factor and rudder normal force using Eq. (8). FN represents the rudder normal force, tR represents the steering resistance deduction factor, and aH is the rudder force increase factor, representing the additional lateral force acting on ship via steering. xR is the longitudinal position of rudder, and xH is the longitudinal acting point of the additional lateral force component.
The rudder normal force is expressed as in Eq. (9). AR represent the rudder area, Λ represents the rudder aspect ratio, while, υR, and uR are the lateral and longitudinal inflow velocity induced by propeller rotation to the rudder, respectively. Resultant inflow velocity to rudder UR can be estimated using Eq. (10). fα represents the rudder lift gradient coefficient. η denotes the ratio of the propeller diameter to rudder span. κ represents the interaction between propeller and rudder. ∈ represents a ration of wake fraction at rudder position to that of the propeller position. αR denotes the effective inflow angle to a rudder. γR is flow straightening coefficient, βR represents the effective inflow angle to rudder in maneuvering motion. wP represents the wake coefficient at propeller position in maneuvering motion. l′R is treated as an experimental constant for expressing υR accurately.
3.6 Sensitivity analysis
A sensitivity index for the standard maneuvering Sijk parameter is estimated using Eq. (11). H* denotes the experimental value of hydrodynamic derivatives. H represents the deviated value of hydrodynamic derivative from experimentally derived value. R* denotes the value of the corresponding maneuvering parameters obtained from standard maneuvering tests such as turning circle and zig-zag. R represents the corresponding values of maneuvering parameters obtained from the maneuvering tests performed using H . Sijk is the sensitivity index for at the ith standard maneuvering parameter for k % change in the jth hydrodynamic derivative. The influence of hydrodynamic derivatives on the standard maneuvering test parameters like tactical diameter, transfer in the case of turning circle and first overshoot angle and time to reach 1st over shoot angle in the case of zig-zag test are considered.
4. Experiment
4.1 Experimental setup
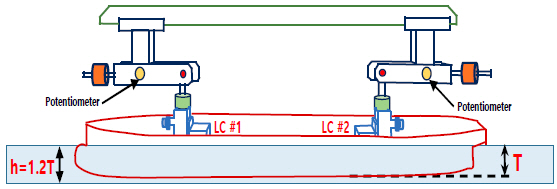
Fig. 4 shows the real experimental setup at h/T = 1.2. In this experiment, the model was attached to the measuring device in the middle of the sub-carriage. Two load cell was used to measure the forces and moments acting on ship hull as shown in Fig. 5.
4.2 Hydrodynamic forces acting on a ship hull
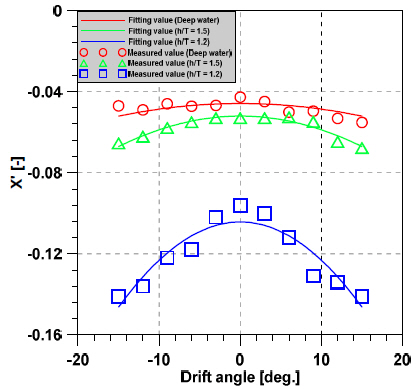
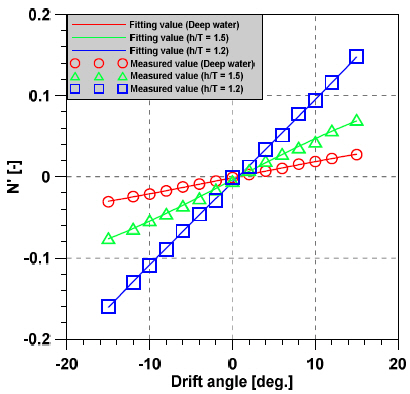
Figs. 6~8 illustrate how the hydrodynamic forces acting on a ship changes as a result of the influence of water depth and drift angle. As the depth becomes shallower, the sway force and yaw moment become larger, particularly in the case of very shallow water (h/T = 1.2). In particular, as the depth of water became shallower and the drift angle increased, the value of yaw moment and sway force also increased.
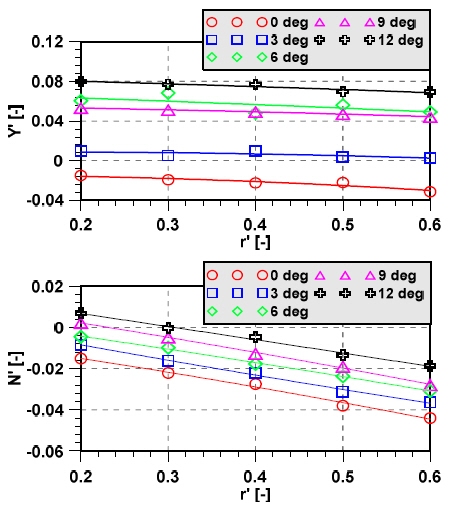
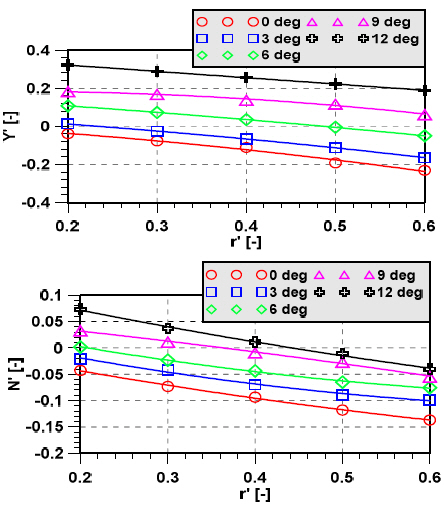
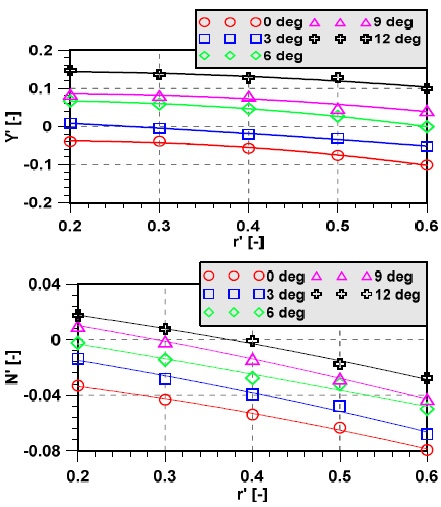
Figs. 9~11 show how the hydrodynamic forces on KVLCC2 changes as a result of various dimensionless angular velocity and drift angle at different water depths. In Figs. 9~11, legends represent the different drift angles such as 0, 3, 6, 9 and 12 degrees. As the depth of water becomes shallower, the hydrodynamic forces on KVLCC2 gradually increases and the angular velocity increases. In contrast, yaw moment significantly increases in very shallow water (h/T = 1.2). The sway force value tends to positive values as the drift angle increase in h/T = 1.5 and h/T = 1.2.
4.3 Hydrodynamic coefficients from model test
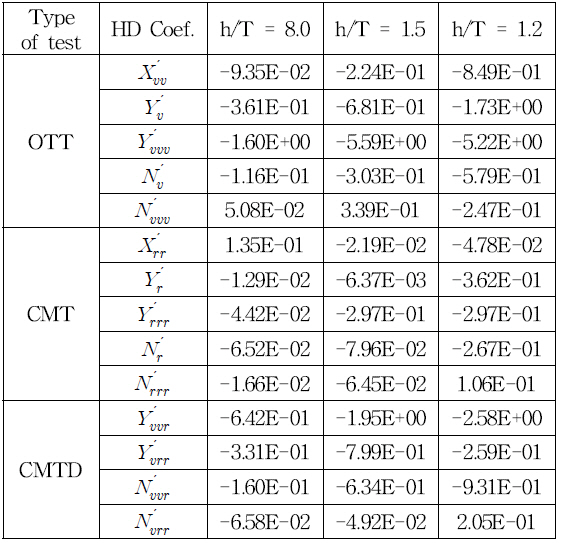
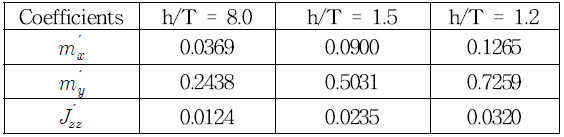
The hydrodynamic coefficients of hull forces at various water depths which are obtained from the model test are listed in Table 3. These hydrodynamic coefficients are applied in the analysis of the sensitivity for all hydrodynamic coefficients on ship maneuvering of KVLLC2 in shallow water. The non-dimensional added mass and added moment of inertia which are estimated using empirical formulas suggested by Li and Wu(1990) are listed in Table 4. When a ship moves through shallow water and confined water, the limited water depth will change the pressure distribution around the ship and the water moves faster under the hull in shallow water based on Bernoulli’s theorem. It means that the velocity under hull bottom increases, and it leads to an increase in hydrodynamic forces of the hull. That is a main reason why the added mass and damping coefficients increase when the ship moves in shallow water.

Non-dimensional added mass and added moment of inertia based Li and Wu’s (1990) empirical formulas
5. Result and Discussion
5.1 Comparison with FRMT
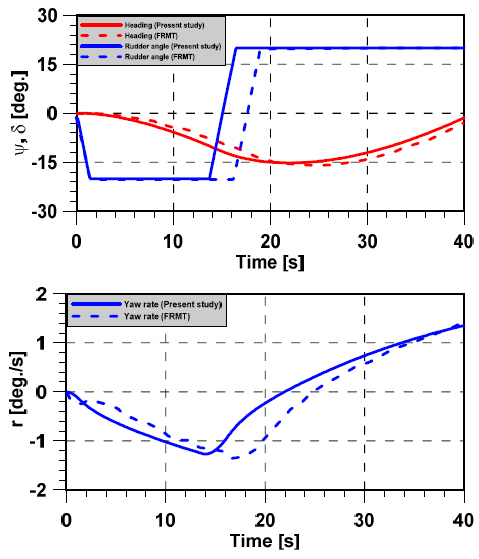
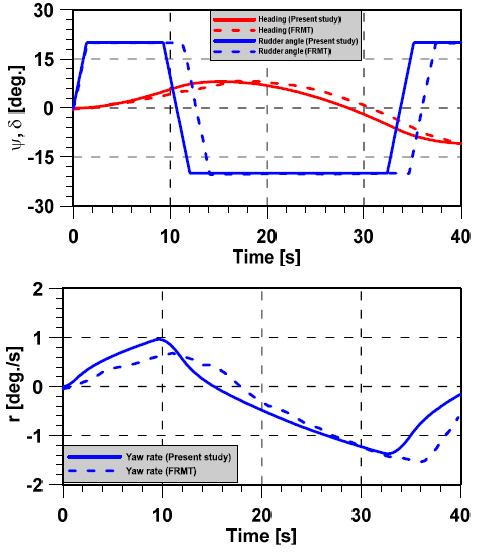
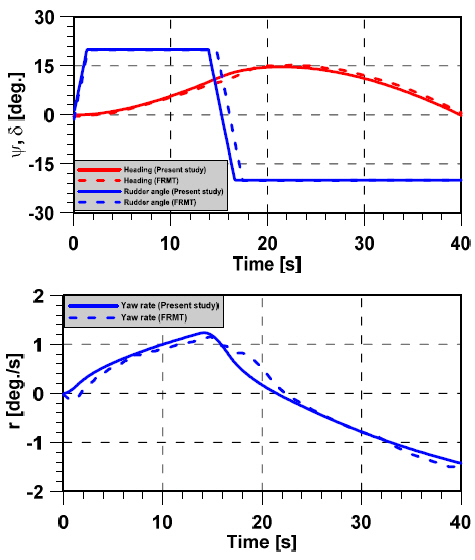
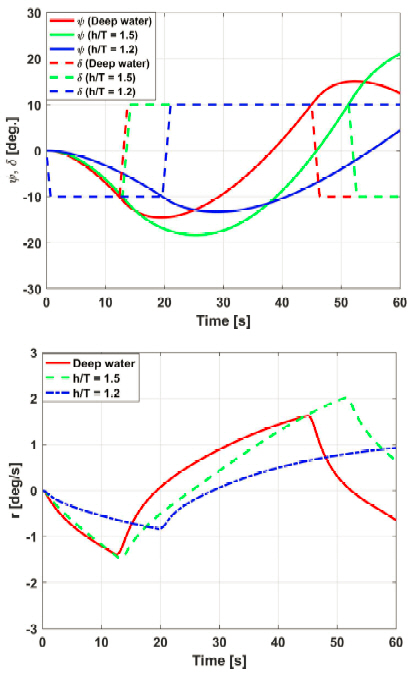
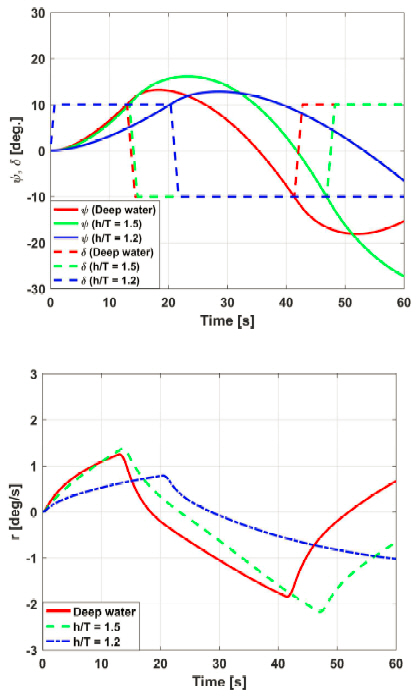
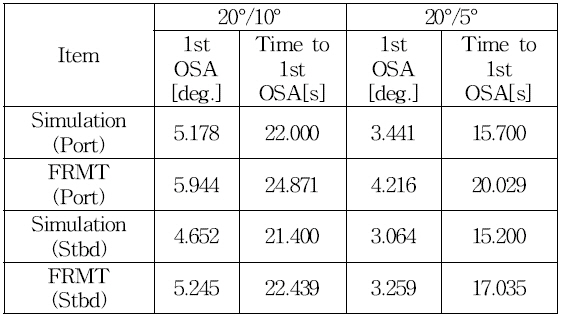
The predicted trajectories of 20o/10o zig-zag and 20o/5o zig-zag are compared with the result of Free Running Model Test(FRMT), which were conducted on the false bottom of KRISO’s towing tank. The result of time histories of heading angle and rudder angle for 20o/10o zig-zag maneuvers are compared with the result of Free Running Model Test(FRMT) by Yeo et al.(2016) as shown in Figs. 12~15. There is a good agreement between Free Running Model Test(FRMT) and simulation obtained by hydrodynamic coefficients from model test conducted in a precise bottom tank in CWNU. As seen in Figs. 12~15, the predicted heading angle and yaw rate of the ship show a similar trend and have the same value as those measured using FRMT by Yeo et al.(2016). The time to 1st Overshoot Angle of FRMT of port and starboard has a little difference, it may be as a result of the starting time of FRMT. The result of 1st Overshoot Angle (OSA) and time to 1st OSA are listed in Table 5.
5.2 Turning test
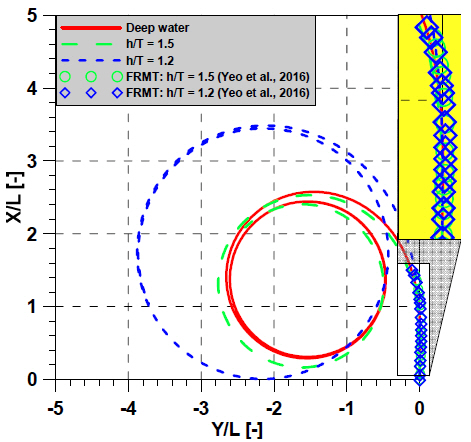
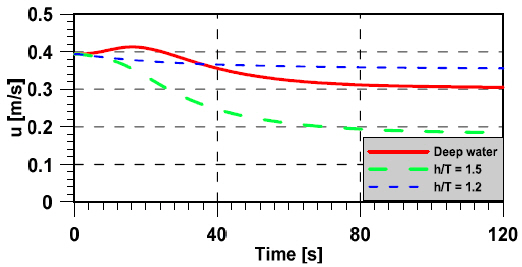
The predicted turning trajectories at various depths of water are compared with result of FRMT which were carried out at in KRISO model basin of KRISO as shown in Figs. 16~19. The result showed that shallow water had a dominant influence on the trajectory of the turning circle, while the advance and tactical diameter dramatically increased when the ship turned in very shallow water (h/T=1.2).
The increased resistance to turning and lateral motion is reflected in the surge velocity and sway velocity of a ship in turning maneuvers. It takes a long time to settle to a constant value in the case of very shallow water as shown in Figs. 16~19. The comparison of advance and tactical diameter at various water depths are listed in Table 6. Advance and tactical diameter in very shallow water increased by 38.46 % and 46.30 %, respectively. Advance and tactical diameter increase with decreasing UKC due to the increase in added mass and damping coefficient of hull forces were as listed in Table 3.
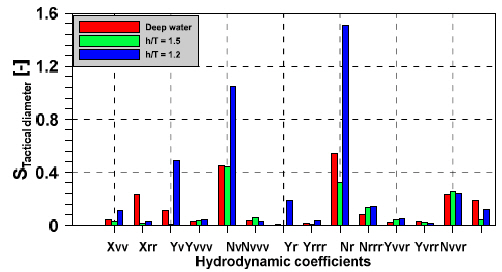
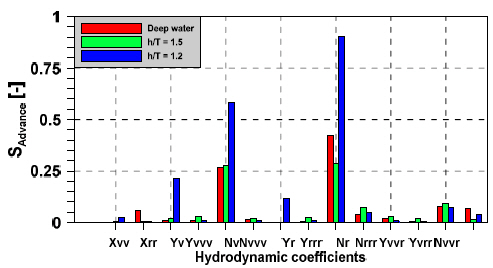
Sensitivity analysis of all hydrodynamic coefficients are done by deviating each hydrodynamic coefficient from the experimental results by increasing 20 %. Figs. 20~21 illustrate the effect of hydrodynamic coefficients on advance and tactical diameter of turning circle. The sensitivity of advance and tactical diameter is highest in very shallow water (h/T=1.2). The hydrodynamic derivatives that mostly affect the advance and tactical diameter are the yaw derivatives,
5.3 Zig-Zag test
The predicted heading angle and yaw rate of 10°/10° zig-zag maneuvers at different water depths are compared to investigate the effect of water depth on 1st Overshoot Angle (OSA) and time to 1st OSA. as shown in Fig. 22~ 23. The result implied that water depth has a dominant influence on 1st OSA ant time to 1st OSA.
The comparison of 1st OSA and time to 1st OSA at various water depths is listed in Table 7. 1st OSA in the 10°/10° zig-zag maneuvers varied as follows: 4.552 degrees in deep water, 8.530 degrees in shallow water, and 3.340 degrees in very shallow water. This result exhibited a similar trend as the sea trial of Esso Osaka in shallow and deep water (Crane, 1979). The time to 1st OSA varied as follows: 19.4s in deep water, 25.4s in shallow water, and 29.0s in very shallow water.
The predicted heading angle and yaw rate of 20°/20° zig-zag maneuvers at different water depths are compared to investigate the effect of water depth on 1st OSA and time to 1st OSA as shown in Figs. 24~25. The result suggested that water depth has a significant influence on 1st OSA and time to 1st OSA.
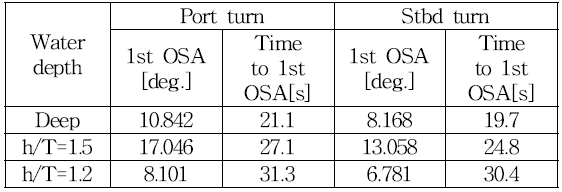
The comparison of 1st OSA and time to 1st OSA at various water depth is listed in Table 8. 1st OSA in the 20°/20° zig-zag maneuvers varied as follows: 10.842 degrees in deep water, 17.046 degrees in shallow water, and 8.101 degrees in very shallow water. These results showed a similar trend to the sea trial of Esso Osaka in shallow and deepwater (Crane, 1979). The time to 1st OSA varied as follows: 21.1s in deep water, 27.1s in shallow water ,and 31.3s in very shallow water.
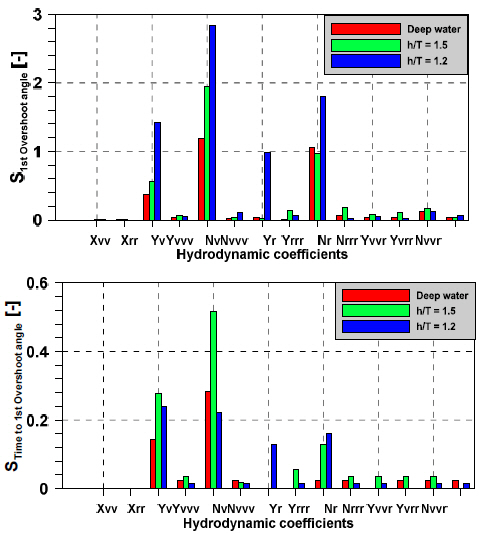
Fig. 26 shows the effect of hydrodynamic coefficients on 1st OSA and time to 1st OSA in 10°/10° zig-zag maneuvers. The hydrodynamic derivatives that commonly affect 1st OSA are the yaw derivatives, N′r , N′υ and sway derivatives, Y′υ and Y′r . Sensitivity of 1st OSA is the highest in very shallow water, hydrodynamic coefficient N′υ and N′r were identified to be sensitive at all water depths, N′υ has highest impact on 1st OSA. In contrast, the hydrodynamic derivatives that commonly affect time to 1st OSA are the yaw derivatives, N′r , N′υ and sway derivatives, Y′υ and Y′r . Sensitivity of time to 1st OSA is highest in shallow water (h/T=1.5), hydrodynamic coefficient N′υ and N′r were identified to be sensitive at all water depths, it has the highest impact on time to 1st OSA.
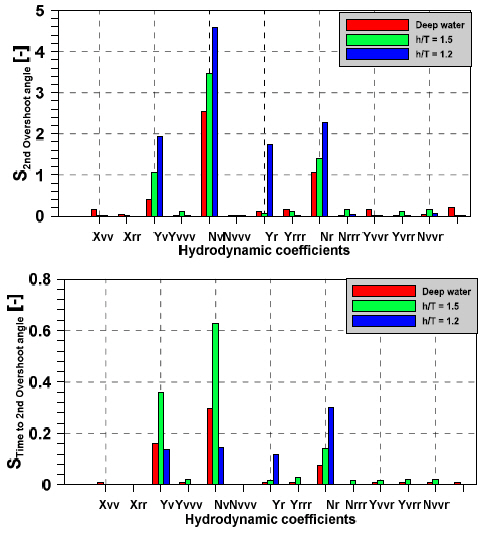
Fig. 27 shows the effect of hydrodynamic coefficients on 2nd OSA and time to 2nd OSA in 10°/10° zig-zag maneuvers. Sensitivity of 2nd OSA is highest in very shallow water, hydrodynamic coefficient N′υ and N′r were identified to be sensitive at all water depths, it has highest impact on 2nd OSA. Conversely, the hydrodynamic derivatives that commonly affect time to 2nd OSA are the yaw derivatives, N′r , N′υ and sway derivatives, Y′υ and Y′r . Sensitivity of time to 2nd OSA is highest in shallow water (h/T = 1.5), hydrodynamic coefficient N′υ and N′r were identified to be sensitive at all water depths, and N′υ has the highest impact on time to 2nd OSA.
In addition, Fig. 28 shows the effect of hydrodynamic coefficients on 1st OSA and time to 1st OSA in 20°/20° zig-zag maneuvers. The hydrodynamic derivatives that commonly affect 1st OSA are the yaw derivatives, N′r , N′υ and sway derivatives, Y′υ and Y′r . Sensitivity of 1st OSA is highest in very shallow water (h/T=1.2), hydrodynamic coefficients N′υ and N′r were identified to be sensitive at all water depths, it has the highest impact on time to 1st OSA. Conversely, the hydrodynamic derivatives that commonly affect time to 1st OSA are the yaw derivatives, N′r , N′υ and sway derivatives, Y′υ and Y′r . Sensitivity of time to 1st OSA is highest in shallow water (h/T=1.5), hydrodynamic coefficient N′υ and N′r were identified to be sensitive at all water depths.
6. Conclusion
In this paper, the model test of KVLCC2 was conducted in Changwon National University’s square tank and the hydrodynamic forces acting on a hull due to the effect of shallow water at low speed was investigated. The concluding remarks are as follows:
First, water depths have a distinct effect on hydrodynamic force on KVLCC2, which significantly affects the ability of a ship to course-keeping and turning abilities at low speed. Particularly, the rate of change is dramatic in very shallow water (h/T=1.2). As the depth become shallower, the value of yaw moment and sway force increase as the depth become shallower and the drift angle increase. Overall, hydrodynamic forces and moments acting on the ship are largest in the case of very shallow water.
Second, hydrodynamic coefficients obtained from model test were used to analyze the sensitivity analysis of all hydrodynamic coefficients on the ship maneuvering of KVLLC2 in shallow water. The simulation of standard maneuvering of KVLLC2 in shallow water was compared with the result of the Free Running Model Test (FRMT) in shallow water from other institutes. There is a good agreement between Free Running Model Test (FRMT) and the simulation obtained through hydrodynamic coefficients from model test which were done in a precise bottom tank in CWNU.
Finally, the standard maneuvering parameters i.e. turning circle and zig-zag maneuvers were conducted at different depths of water and their effects on the standard maneuvering parameters estimated to appreciate the importance of various derivatives in ship maneuvering in shallow water. The hydrodynamic derivatives that mostly affect the advance and tactical diameter are the yaw derivatives,
Acknowledgements
This research is financially supported by Changwon National University in 2019~2020.