|
 |
| J Navig Port Res > Volume 45(1); 2021 > Article |
|
요 약
동유체력 미계수는 수중운동체의 조종성능을 예측하기 위해 정확히 추정되어져야 하며 추정 방법의 일환으로 다양한 모형시험이 수행되어오고 있다. 수중운동체는 횡동요 모멘트 변화에 민감하므로 관련 동유체력 미계수를 추정하는 작업은 정확히 수행되어져야 한다. 본 연구에서는 횡동요 운동과 관련한 동유체력 미계수를 간단하게 추정할 수 있는 순수 횡동요 장비를 새롭게 설계하였다. 횡동요 운동은 간단한 기계적 메커니즘을 통하여 구현하였으며, 메커니즘의 원리와 적용과정 그리고 설계한 장비의 system identification에 대해 기술하였다. 또한 순수 횡동요 시험의 해석방법을 제시하고 설계한 장비에 대해 반복시험을 거쳐 결과의 재현성을 확인하였다.
ABSTRACT
Hydrodynamic coefficients should be accurately estimated to predict the maneuverability of underwater vehicles. Various captive model tests have been performed as part of estimation methods for these coefficients. Estimating hydrodynamic coefficients related to roll motion is important because underwater vehicles are sensitive to changes of roll moment. In this research, a pure roll motion equipment was newly designed to simply estimate hydrodynamic coefficients with respect to roll motion. Roll motion was implemented through a brief mechanical mechanism. The principle of operation, application process, and system identification of the equipment are described. An analysis method of the pure roll test is also suggested. Repeated tests of the newly equipment were carried out to check its reproducibility.
수중운동체와 관련된 연구는 지속적으로 이루어져 왔으나, 기존에는 잠수함 및 어뢰와 관련된 연구개발이 집중적이었다. 하지만 최근 들어 기존 군사용으로 이용되는 잠수함이나 어뢰로서의 목적을 넘어, 해양자원 개발과 해저탐사 및 정찰 등 다양한 분야로 진출함에 따라 수중운동체에 대한 관심은 국방기술 뿐만이 아닌 경제적, 산업적인 요소로서 작용하기 시작했다. 특히, 기존 자원의 고갈로 인해 심해자원과 같은 새로운 자원 확보에 대한 목소리가 대두되며 관련 수요는 자연스레 수중운동체 플랫폼 연구의 확장을 광범위하게 이끌었다. 현재에도 국내외 많은 연구기관에서 다양한 목적아래 수중운동체의 핵심 기술 연구가 수행되어 오고 있다.(Fossen, T. I., 1995;수중운동체 연구에 있어 근본이 되는 조종성능에 대한 관심이 높으며 1960년대를 기점으로 현재에도 관련 분야에 대한 연구가 활발하게 진행되어오고 있다.
Gertler and Hagen(1967)은 수중체에 작용하는 동유체력을 관련한 변수의 테일러 전개를 통하여 다항식 모형으로 제시하였다. Feldman(1979)는 수중체에 작용하는 비선형적인 요소들을 반영하고자 Gertler and Hagen이 제시한 모델에 식을 추가하거나 수정하였다. 이 외 Watt(2007)는 잠수체의 운동면을 국한시키지 않는 방식으로 가해지는 동유체력 모델을 정립하였다. 더불어 Healey and Lienard(1993)은 저속으로 주행하는 대형 AUV의 운동방정식을 제시하였으며 이 외에도 많은 국내외 연구소에서 다양한 수중운동체의 운동방정식에 대한 연구를 수행해오고 있다. 수중운동체의 조종성능을 가장 정확히 확인할 수 있는 방법은 실해역에서 직접 실험하는 것이다. 하지만 결과도출까지 소요되는 시간적, 경제적 비용이 상당하기 때문에 수조모형시험이나 Computational Fluid Dynamics(CFD) 해석 등 다양한 방법을 통하는 것이 일반적이다. 수중운동체의 조종성능 예측을 위해서는 수중운동체의 운동방정식을 적절하게 세우는 것이 중요하며(Ohtsu, K. et al., 1996; Mogens et al., 2000; Lee, S. K. 2010) 다양한 상황에서의 수조모형시험 혹은 CFD를 통해 운동방정식을 구성하는 동유체력 미계수를 도출하는 것에서 시작한다. 수중운동체의 동유체력 미계수를 얻는 구속 모형시험 종류로서 정적시험으로는 대표적으로 저항시험, 정적 영각시험 등이 존재하며, 동적시험으로는 PMM(Planar motion mechanism)시험과 강제선회(Rotating arm)시험을 비롯한 시험들이 존재한다. 해당 구속 모형 시험들은 예인수조 혹은 CPMC(Computerized Planar Motion Carriage)에서 행해지며 각 시험을 통해 도출할 수 있는 동유체력 미계수의 종류가 다르며 시험설비 상의 장단점이 존재한다. 이 외에도 다양한 구속 모형 시험들에 대한 방법이 국내외적으로 꾸준히 제시되며 수행되고 있다. 구속 모형 시험을 통한 국내연구로서는 기본적으로 PMM 시험을 수행하는 연구가 많이 이루어져 왔으며 (Lee and Kwon., 2002, Jung et al., 2014(a); Jung et al., 2014(b); Park et al., 2020;) 해당 결과들은 잠수함의 초기 선형 설계 당시 운동성능을 확인하는 수단으로 사용되었다. 최근에는 CPMC를 이용한 수중운동체의 구속모형시험을 통해 다양한 선형 및 비선형 동유체력 미계수를 도출하는 연구가 활발히 진행돼 오고 있다. (Kim et al., 2009; Jeon et al., 2017) 최근에는 몰수체의 횡동요 운동과 관련한 동유체력 미계수를 추정할 수 있는 원추형 시험장비(Coning Motion test)를 통한 연구 또한 진행되었다.(Park et al., 2015) 보통 상하동요, 종동요, 좌우동요, 선수동요와 관련한 동유체력 계수들을 추정하던 구속모형시험이 주를 이루고 횡동요의 경우 원추형 시험 장비를 제외하고는 보통 별도의 장비없이 PMM장비에 추가적으로 횡동요 운동을 구현하는 메커니즘을 설치한다. 해당 방식의 경우 스트럿에 수중체를 연결시키기 때문에 프로펠러 회전을 할 수 있다는 장점이 있으나 한 방향 회전 시험은 불가능 하다는 한계가 있다.
수중운동체는 횡동요 방향으로의 복원 모멘트, 감쇠모멘트 그리고 관성 모멘트는 작은 값을 갖기 때문에 작용하는 횡동요 모멘트 변화에 굉장히 민감하다. 그러므로 횡동요 운동과 관련한 동유체력 미계수를 정확히 추정하는 작업은 반드시 수행돼야 한다.
본 논문에서는 수중체의 횡동요 운동과 관련한 동유체력 정립에 있어 동유체력 미계수를 도출하기 위해 수중체에 순수 횡동요 운동을 강제하는 장비를 설계하는 과정을 기술하였다. 해당 장비 설계에 있어 정현적 강제운동을 서보모터를 통하여 제어하지 않고 간단한 기계적 메커니즘만을 이용하여 구현하였으며, 관련 메커니즘과 적용 과정에 대해 자세히 기술하였다. 설계한 장비는 2차원 도면을 Auto CAD로 설계하였으며, 설계 적정성을 사전에 고려하여 제작하였다. 추가로 제작된 장비의 재현성을 검증하기 위하여 순수 횡동요 시험을 3회 반복 수행하였으며 결과를 통해 새롭게 제작한 순수 횡동요 장치의 재현성이 우수함을 확인하였다.
구속 모형 시험을 통해 순수 횡동요를 가하는 데에는 다양한 방식이 존재한다. 이 중 서보모터를 이용하여 직접 제어를 통해 정현적 운동을 구현하는 방식이 대부분이다. 하지만 이와 같이 서보모터를 직접 회전축에 연결하여 조화운동을 구현할 시 서보모터의 회전각, 회전속도 등을 실시간으로 피드백 받아 제어를 해야하므로 제어 시스템이 복잡해지고, 무엇보다 구현하려는 각속도의 유지를 위해 서보모터에서 발생되는 토크가 매우 불규칙한 임펄스형태로 발생할 수 있다는 문제점이 존재한다. 본 논문에서 소개할 장비의 경우, 순수 횡동요만을 구현한다는 목적에 기반하여 기존의 서보모터를 이용해 직접적인 제어방식으로 운동을 구현하는 구속 모형 장비와 달리, 경제적이고 상당히 간단한 기계 메커니즘을 이용하여 모형에 순수 횡동요만을 가할 수 있도록 설계하였으며 이로 인해 직접적인 제어방식에서 발생할 수 있는 문제점들을 해결하였다.
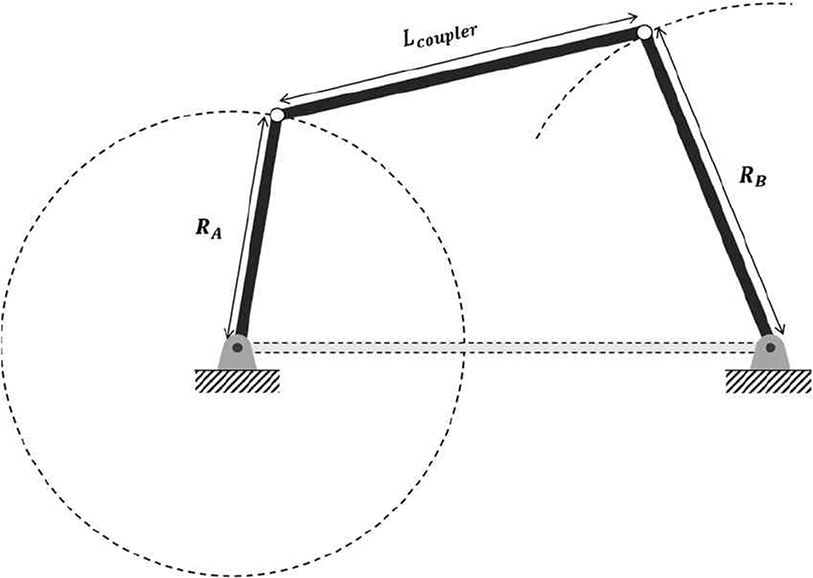
Fig. 1은 4 bar mechanism의 원리를 도시한 것이다. 해당 메커니즘은 4개의 Link를 통해 구현한 기계적 메커니즘으로 운동의 방향을 전환하거나 다른 기계적 이점을 얻기 위해 사용된다. 해당 구동 방식은 Link를 사용하여 운동 시 마찰력을 최소화하고 높은 구동 신뢰성을 확보할 수 있는 이점을 가진다. 뿐만 아니라 직관적인 구조로 인하여 설계 및 이해에 있어 용이하고 이는 수학적 해석을 단순화 할 수 있다는 장점이 있다. 필요에 따라 보다 더 큰 하중을 수용할 수 있어 기계 장치의 구동 원리로 널리 사용되고 있다. 다양한 방식의 4 bar mechanism 중에서 본 장비를 개발함에 있어 사용된 메커니즘은 Grashof mechanism(Crank rocker mechanism)으로 식(2.1) 기준을 따른다.(Natesan, 1994)
이 때, Lmax는 가장 긴 Link의 길이, Lmin는 가장 짧은 Link의 길이, La과 Lb은 각각 나머지 두 Link의 길이를 나타낸다. Crank rocker mechanism에서 길이가 가장 짧은 Link가 구동을 담당하는 구동 Link의 역할을 한다. 길이가 가장 짧은 Link가 회전운동을 하면 맞은편에 위치한 Link는 구동 Link의 회전 운동과 같은 주기를 갖는 조화 운동을 한다.
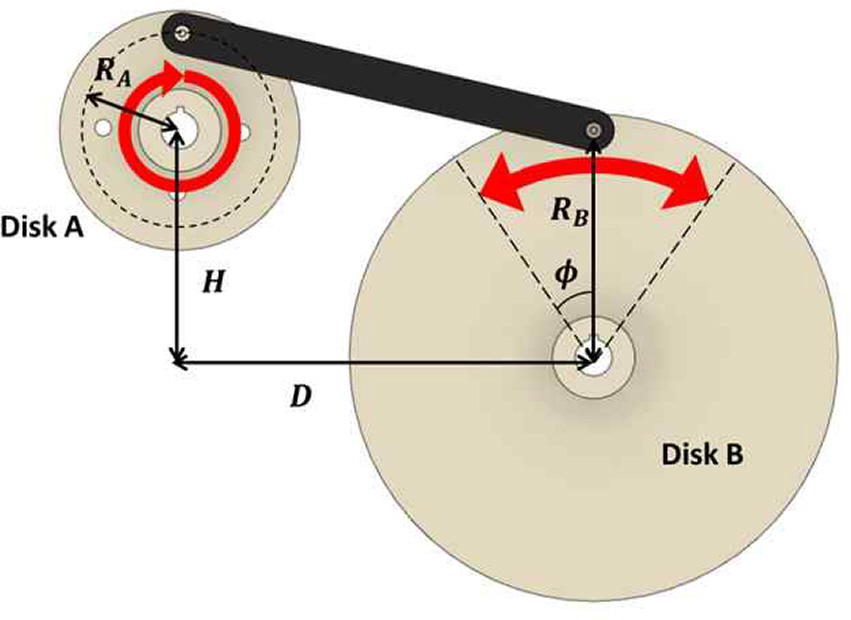
Fig. 2는 실제 본 장비 설계에 있어 4 bar mechanism을 적용한 모습으로 모터와 연결된 Disk A를 한 방향으로 회전시키고, Link를 통해 연결된 Disk B를 조화 운동시켜 일정 주기의 횡동요 운동을 구현하였다. RB는 횡동요를 구현하는 Disk B의 반지름이며 RA는 한 방향으로 회전하는 Disk A의 반지름이다. L은 연결부 링크의 길이를 나타내며 D는 각 Disk 중심 간 수평거리이며 H는 각 Disk간 수직 거리를 나타낸다. θ는 지속적으로 한 방향으로 회전하는 구동부의 각도, α는 연결부 링크가 지면과 이루는 각도 그리고 ϕ는 횡동요 각도를 의미한다.
수치 계산은 Disk A 위의 한 점을 중심으로 하여 Coupler Link의 길이와 같은 크기의 반지름을 갖는 원과 Disk B와의 교점의 좌표를 각 Time step마다 구하여 조화운동의 자취를 나타내었으며 이를 통해 계획된 Stroke 조건을 구현할 수 있는지 확인하였다. 입력에 해당하는 구동부 회전 각 θ와 출력에 해당하는 횡동요 각 ϕ와의 관계는 다음과 같이 기술할 수 있으며 해당 관계식은 Freudenstein’s equation으로 알려져 있다. (Freudenstein, 1955)
양 변을 제곱하여 더한 후 α를 소거하여 ϕ에 대해 나타낸 식(2.4)로 정리할 수 있으며, θ로 이루어진 계수 k1(θ), k2(θ) 그리고 k3(θ)는 식(2.5)에 나타내었다.
최종적으로 구동부의 한 방향 회전각 θ에 따른 출력단 횡요 각 ϕ의 관계식은 식(2.6)과 같이 도출할 수 있다.
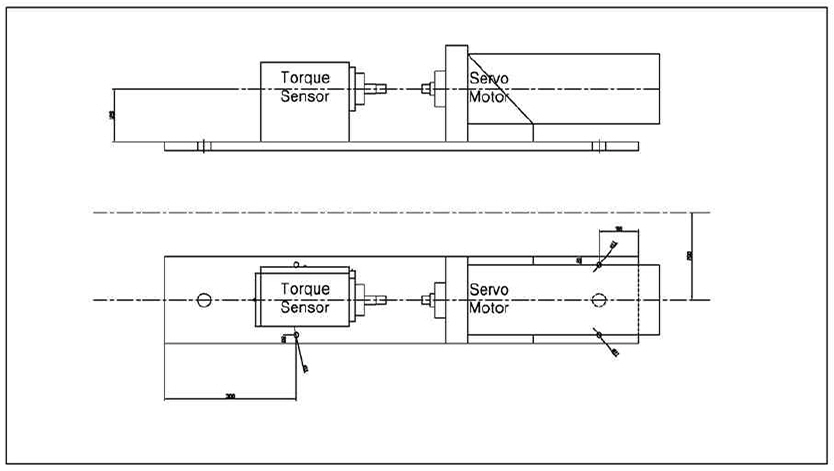
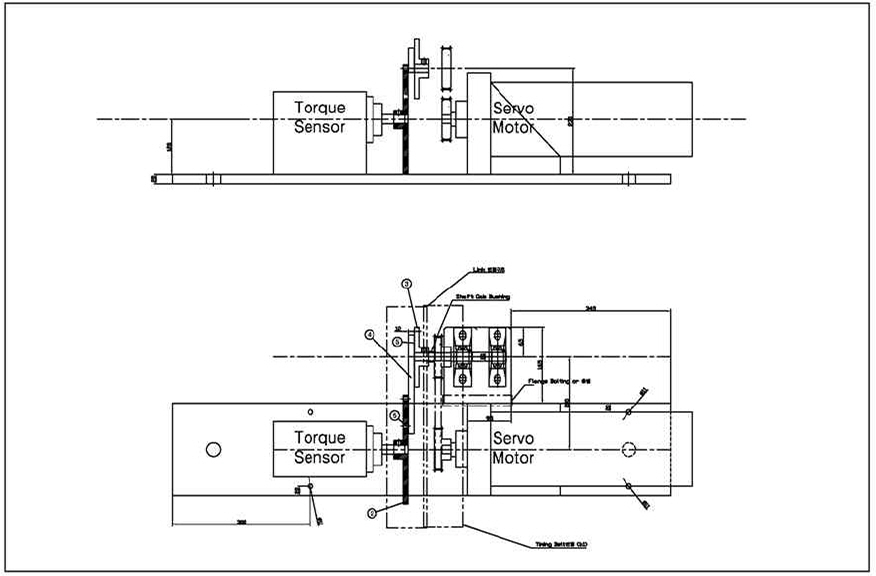
Fig. 4는 앞서 기술한 4 bar mechanism을 적용하기 전 순수 횡동요 시험장비를 구성하는 기본 장비의 위치 및 컨셉을 나타낸 2차원 평면도이다. 한 방향으로 축을 회전시키기 위해 감속기와 결합한 서보모터가 장비 뒷쪽에 위치하며 토크 센서가 앞쪽에 위치한다. 토크 센서를 4 bar mechanism 전방에 설치함으로써 모델에 작용하는 유체력을 곧바로 측정할 수 있다. 기계적인 장비에서 발생할 수 있는 요소들은 system identification을 통해서 고려하였다.
Fig. 5는 해당 평면도와 대응하는 스냅샷이다. 토크 센서와 서보모터의 빈 공간에 앞서 기술한 4 bar mechanism을 구현하는 장비가 위치하게 된다.
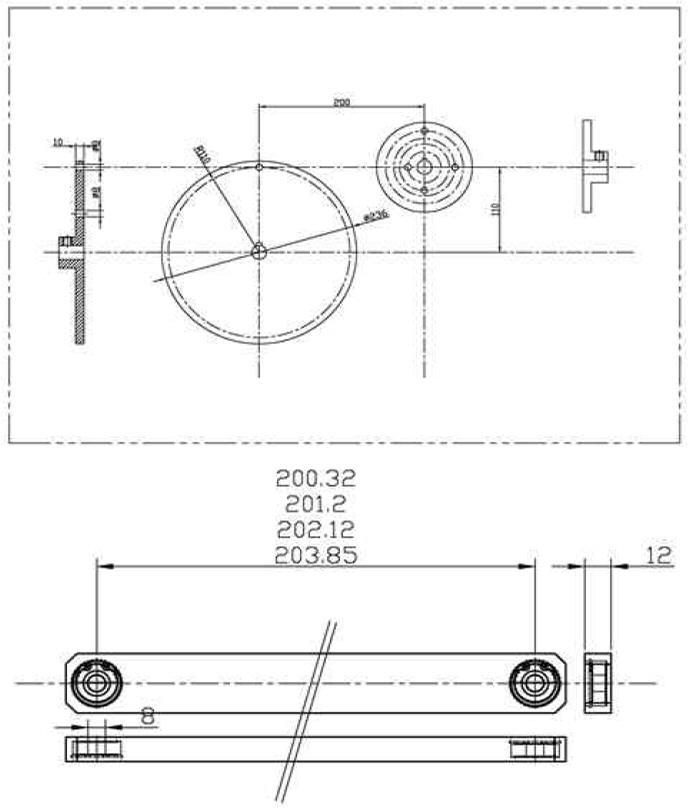
Fig. 6은 결정한 Table. 1과 대응되는 값의 Disk와 Link의 2차원 설계 도면을 나타낸 것이다. Fig. 7은 Disk 간의 위치를 앞서 결정한 D와 H에 위치시킬 수 있도록 연결부를 만든 다음, 4 bar mechanism을 구현할 수 있도록 토크 센서와 서보모터 사이에 위치시킨 것이며 Fig. 8은 실제 설계를 완료한 모습이다. 서보모터 쪽 Disk A와 직경이 같은 구동 디스크 부분과 Disk A와의 연결은 Timing belt를 이용하였다.
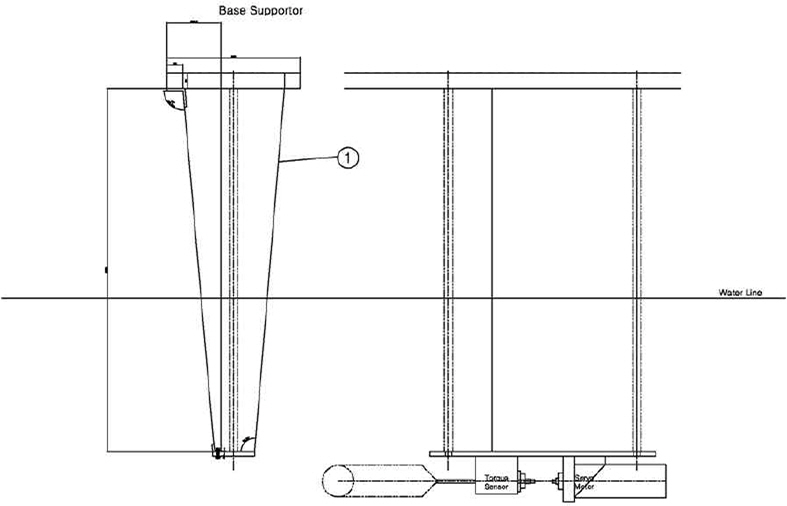
구속 모형 시험의 경우 자유 표면으로 부터의 영향을 벗어나고자 심도를 맞추어 시험을 진행해야 한다. 횡동요 운동 시 발생하는 진동을 최소화하기 위해 base supporter를 제작하여 연결하였다. Fig. 9에는 base supporter의 2차원 설계 도면과 도면 내 적용한 모습을 나타낸 것이며, Fig. 10은 실제 실험에서 base supporter(적색 점선 표기)를 장비 앞쪽에 2개, 뒷쪽에 2개 총 4개를 설치하여 장비를 고정한 모습을 나타낸 것 이다. 이를 통해 예인과 횡동요를 동시에 해야 하는 본 실험의 경우에도 장비의 진동 없이 안정적이게 실험을 진행하였다. Fig. 11은 계획한 형태로 장비 셋업을 모두 마친 스냅샷이며 서보모터와 토크센서 그리고 4 bar mechanism의 위치를 나타내었다.
앞서 기술한 기계적 메커니즘으로 설계한 순수 횡동요 장비의 구현이 실제 정현 운동의 수학적 모델과 얼마나 일치하는 가를 검증하는 작업을 수행하였으며 그 결과를 Fig. 12에 도시하였다. Fig. 12의 적색 실선은 진폭 약 10°의 정현 운동을 수학적으로 도시한 것이며 녹색 실선은 제작한 장비를 통해 구현되는 실제 횡동요 각을, 청색 실선은 식(2.6)에 의해 도출되는 횡동요 각을 나타낸다. 녹색 실선과 청색 실선이 잘 일치하므로 이를 통해 설계 및 가공이 정확히 이루어졌음을 확인할 수 있다. (a)에는 횡동요 각 변위의 시계열 비교 정보를 나타내었으며, (b),(c)에는 횡동요 각속도, 각가속도를 계산하여 함께 도시하였다. (b),(c)에서의 녹색 실선 결과는 (a)에서 얻은 각 변위를 중앙차분법을 적용하여 구하였다. Fig. 12에서 확인할 수 있듯, 4 bar mechanism을 활용한 횡동요 구현이 정현운동과 근사함을 확인할 수 있다.
순수 횡동요 시험(Pure roll test)은 수중 운동체를 일정 속도로 예인하는 동시에 특정 각도 범위로 횡동요만을 강제하여 수중운동체의 운동방정식 중 횡동요 성분과 관련한 미계수를 추정하는 시험이다. 해당 시험을 통하여 횡동요 부가관성모멘트인 K p ˙ ' K p '
순수 횡동요 시험은 예인수조에서 수중운동체의 다른 운동은 구속시킨 채, 오로지 모델을 예인하는 동시에 횡동요 각을 정현적(Sinusoidal motion)으로 부가하여 실시할 수 있다.
수중운동체는 횡동요 성분을 제외한 다른 모든 성분들이 구속되어 있으므로 v,q,w,r등의 성분들을 0으로 고정할 수 있다. Fig. 13에서 보여지 듯, ϕo는 횡동요 진폭을 나타내며 T는 횡동요 주기를 나타낸다.
식(3.1), 식(3.2)와 같이 순수 횡동요 시험에 맞게 순수한 횡동요 성분을 제외한 성분들과 횡동요 각, 각속도, 각가속도를 모델링 할 수 있다. 최대한 간단하게 동유체력 미계수를 추정하기 위한 방법으로는 식(3.1)와 식(3.2)을 횡동요 동유체력 모델(Healey., 1993) 인 식(3.3)에 대입 후 정리하였다. 본 구속 모형 시험 장비는 순수 횡동요를 구현하므로, 횡동요와 관련하지 않은 다른 교차항과 추진기 및 타력에 관련한 항들을 제외하고 유체정역학 성분 또한 본 수중운동체 모형의 무게중심과 부력중심의 y축, z축 성분을 각각 동일하게 맞추어 설계하였기 때문에 소거하였다. 따라서 식(3.3)은 식(3.4), 식(3.5)로 간단화 할 수 있다. 본 장비의 경우 모형에 sting을 삽입하여 운동을 강제하기 때문에 프로펠러로 인한 영향은 배제하였으며 타로 인한 영향을 나타내는 유체력 미계수 또한 생략하였다. 식(3.4)와 식(3.5)는 차원화한 결과이며 이는 SNAME(1950)에 따라 무차원화하였다.
KE는 수중운동체가 횡동요 할 때 외부에서 가해지는 모멘트이므로 본 장비의 토크미터를 통해서 측정되어지는 모멘트이다. 선형화 식(3.5)에서 KE에 대해 푸리에 해석을 적용하면 부가한 횡동요 진폭과 동위상(In-phase)을 갖는 성분과 반위상(Out-phase)을 갖는 성분으로 식(3.6)과 같이 나눌 수 있다. 이 때 물리적 의미를 살펴보면 각변위 ϕ와 동위상 성분은 횡동요 가속도에 관련하므로 관성항에 해당하고, 각변위와 90°의 위상 차이가 나는 반위상 성분은 횡동요 속도와 관련하므로 감쇠항에 해당함을 알 수 있다.
식(3.6)을 식(3.4), 식(3.5)에 대입하여 식 전체를 무차원화 한 결과는 식(3.7)과 동일하며, 부가한 각변위 ϕ와 동위상 및 반위상 성분끼리 비교한 결과는 각각 식(3.8), 식(3.9)와 같다.
수중운동체 시험의 경우 기계장비를 통해 횡동요를 구현하게 되고. 이에 따라 발생하게 되는 횡동요 모멘트에는 순수 동유체력(KE) 외에 기계적 장비에 의해 발생하는 토크 또한 측정 결과에 포함이 되어있다. 본 논문에서는 해당 항을 Kmechanical라 표기하였으며 이를 식으로 표현하면 식(3.11)과 식(3.12)와 같다.
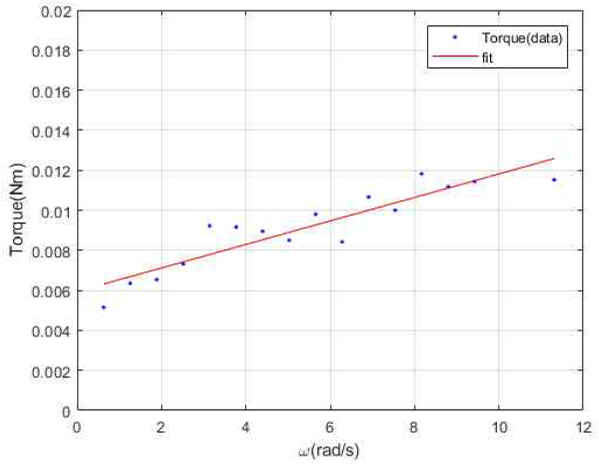
따라서 측정한 횡동요 모멘트(Kmeasure)에서 기계적 장비에 의해 발생하는 Kmechanical를 제외해야만 수중운동체에 작용하는 순수 동유체력을 얻을 수 있다. Kmechanical에는 스팅부분의 조화운동으로 인한 관성력과 기계적 장비에 의한 감쇠력이 포함되어 있다. 이에 관한 운동방정식은 식(3.13)과 같이 표현할 수 있으며, Ixx, shaft는 모형을 제외한 채 토크센서로부터 전방에 위치하는 플랜지와 스팅의 질량관성모멘트를 의미하고 cmech는 기계 장비로 인해 발생하는 감쇠계수를 의미한다. Ixx, shaft는 사전에 계산할 수 있으며, 감쇠모델인 cmech를 추정해야만 하는데, 이는 모형을 부착하지 않은 채 다양한 각속도에서의 한 방향 회전 시험을 통해 도출할 수 있다. Fig. 16에는 본 시험에서 cmech 도출을 위해 수행한 한 방향 시험 결과를 나타내었으며, 선형 최소자승법을 통하여 회귀하였다. Fig. 16의 y절편은 Coulomb force τcoulomb에 해당하며, 해당 결과 또한 기계 장비의 영향으로 고려해야 한다.
운동방정식을 기계 장비에 의한 영향을 포함시킨 운동방정식으로 다시 표현하면 식(3.14)와 같으며, 사전에 계산할 수 있는 Ixx, shaft와 추정한 cmech를 통해 조화운동에서 기계 장비에 의해 발생하는 요소를 제거하여 순수 동유체력을 획득할 수 있다.
Fig. 17에는 본 실험에 적용한 Kmechanical의 결과를 도시하였다. 실험을 진행하여 측정한 Kmeasure (하늘색)와 이를 푸리에 해석한 결과(청색), 기계 장비에 의해 발생하는 Kmechanical (녹색)을 (a)에 나타내었으며 (b)에는 측정결과 Kmeasure에서 Kmechanical를 뺀 후 푸리에 해석을 적용한 결과를(적색) 추가하여 도시하였다. 해당 적색 실선 결과가 곧 순수 동유체력(KE)이 된다.
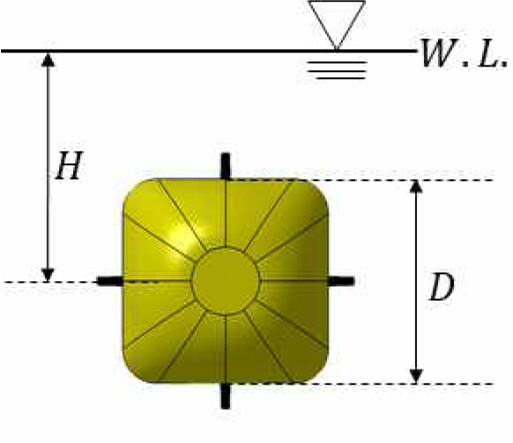
본 논문에서는 기계적 메커니즘을 활용한 순수 횡동요 시험 장비를 이용하여 검증 시험을 진행하였다. 시험 수행은 부산대학교 선박예인수조동의 길이 100m 폭 8m 깊이 3.5m의 제원을 가진 예인수조(PNMB)에서 진행되었다. Fig. 18은 부산대학교 예인수조의 스냅샷이다. Fig. 19(a)는 실험 셋업을 모두 마친 스냅샷이며 Fig. 19(b)는 자유표면의 영향을 배제하기 위해 심도 5에 맞추어 수중체를 잠수시킨 후 시험을 수행하는 모습이다. Fig. 20에는 심도의 의미를 도식적으로 나타내었다. 심도는 수면과 수중운동체 중심까지의 높이(H)와 수중운동체의 정면 직경(D)에 대한 비로써 정의한다.
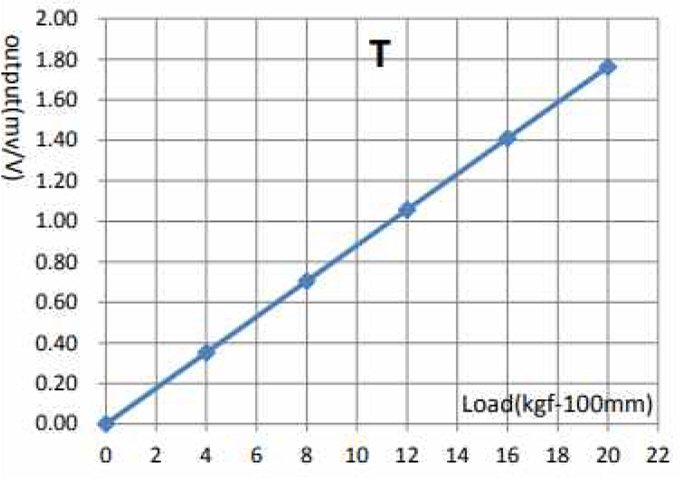
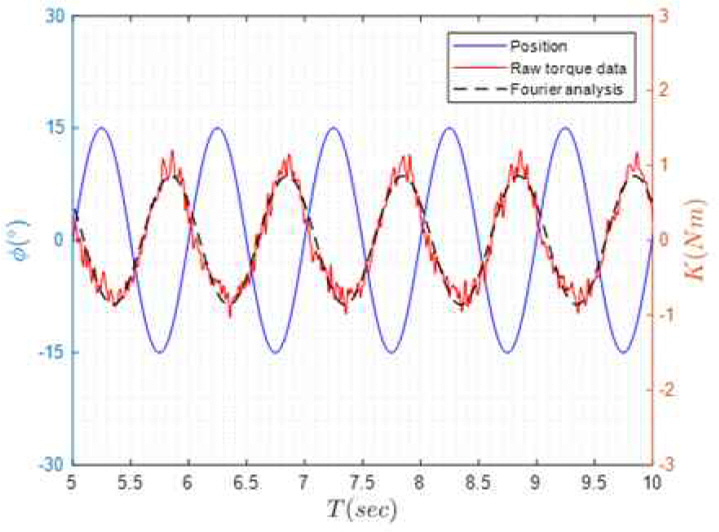
제작된 순수 횡동요 장치의 성능을 확인하기 위한 검증시험을 수행하였다. 검증 시험은 정현적 운동에 대해 예인속도 1.0 m/s, 횡동요 각 진폭 15°, 횡동요 주기 1초의 시험 조건에서 수행되었다. 실험 오차를 확인하기 위해 반복 3회 실험을 통해 횡동요 모멘트 및 횡동요 각변위를 측정하였다. Fig. 21은 검증 시험의 계측 결과를 도시한 것이다. 청색 실선은 횡동요 각 변위를 의미하며 엔코더를 통해 계측한 각변위 시계열 또한 진폭 15°가 잘 구현됨을 알 수 있다. 적색 실선은 실제 실험을 통해 측정한 횡동요 모멘트이고 흑색 실선은 해당 결과를 푸리에 해석한 것이다.
본 논문에서는 순수 횡동요만을 구현하는 장비를 단순한 기계 매커니즘인 4 bar mechanism을 활용하여 제작하고 횡동요 실험을 수행하여 장비의 설계가 목적에 부합하였음을 보였다. 더불어 기계 장비로 인해 발생하는 성분들에 대한 system identification을 진행하는 과정과 순수 횡동요 시험의 해석 방법에 대해서도 기술하였다. 제작된 장비의 재현성을 검증하기 위하여 순수 횡동요 시험을 3회 반복 수행하였으며 도출한 결과를 통해 해당 장비를 통한 실험결과가 반복성을 가짐을 확인하였다. 개발된 순수 횡동요 구속 모형 장비를 활용하여 수중체의 횡동요 운동과 관련한 동유체력 미계수를 보다 쉽게 도출할 수 있게 되었다. 그러나 본 장비의 경우 스팅 타입의 연결 방식을 채택했기 때문에 추진기로 인한 후류가 수중체의 조종운동에 미치는 영향을 포함한 동유체력 미계수를 추정하기에는 한계가 있다. 앞으로의 연구에 있어 스팅에 추진기를 달아 후류를 모사할 수 있는 방안을 추가적으로 고안한다면, 해당 장비를 이용하여 좀 더 정확한 동유체력 미계수를 추정할 수 있을 거라 사료된다.
Fig. 12.
Verification of sinusoidal motion (a) roll angle (b) angular velocity (c) angular acceleration
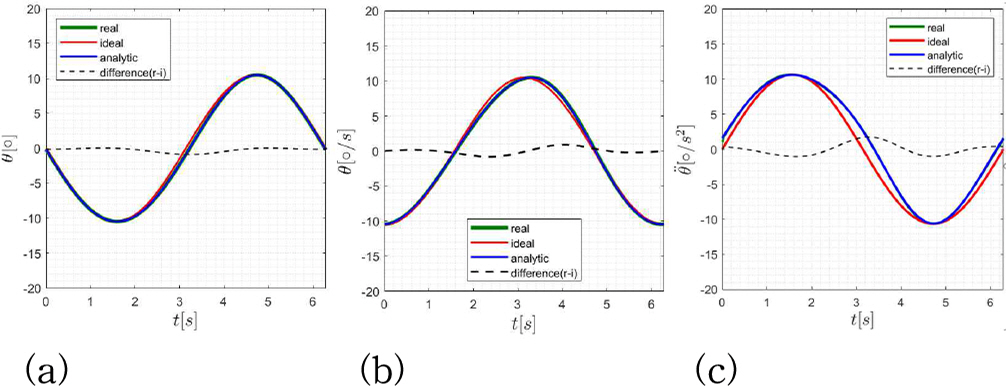
Table 1.
Parameter values of 4 bar mechanism
| D [mm] | H [mm] | RA [mm] | RB[mm] | ϕo [°] |
|---|---|---|---|---|
| 200 | 110 | 20 | 110 | 10 |
| 200 | 110 | 30 | 110 | 15 |
| 200 | 110 | 37 | 110 | 20 |
References
[1] Bae, JY and Shon, KH(2008), ““A Study on Manoeuvering Motion Characteristics of Manta-type Unmanned Undersea Vehicle””, Journal of the Society of Naval Architects of Korea, Vol. 46, No. 2, pp. 114-26.

[4] Fossen, TI(1975), “Guidance and Control of Ocean Vehicle”. JOHN WILEY & SONS.
[5] Foujino, M(1975), ““The Effect of Frequency Dependence of the Stability Derivatives on Maneuvering Motion””, ISP, Vol. 22.

[6] Freudenstein, F(1955), ““ Approximate synthesis of four-bar linkages””, ASME, Vol. 77, pp. 853-861.
[7] Gertler, M and Hagen, GR1967), “Standard Equations of Motion for Submarine Simulation”, NSRDC-Report SR 009 01, 01 Task 0102..

[8] Healey, AJ and Lienard, D(1993), ““Multivariable Sliding-Mode Control for Autonomous Underwater Vehicles””, IEEE Journal of Ocean Engineering, Vol. 18, No. 3, pp. 327-339.
[9] Jung, JW, Jeong, JH, Kim, IG and Lee, SK(2014a), ““Estimation of Hydrodynamic Derivatives of Submarine Model by Using VPMM Test””, Journal of Navigation and Port Research, Vol. 39, No. 3, pp. 173-178.

[10] Jung, JW, Jeong, JH, Kim, IG and Lee, SK(2014b), ““Experimental Study on Hydrodynamic Coefficients of Autonomous Underwater Glider Using Vertical Planar Motion Mechanism Test””, Journal of Ocean Engineering and Technology, Vol. 28, No. 2, pp. 119-125.

[11] Jeon, MJ and et al(2017), ““Study on Maneuvering Characteristics of Submerged Body by changing its Design Parameters””, Journal of Ocean Engineering and Technology, Vol. 31, No. 2, pp. 155-163.

[12] Kim, YG and et al(2009), ““Prediction of Maneuverability of KCS by CPMC Captive Model Test””, Journal of the Society of Naval Architects of Korea, Vol. 46, No. 6, pp. 553-561.

[13] Lee, TI and Kwon, SH(2002), ““A Study on Practical PMM Test Technique for Ship Maneuverability Using System Identification Method””, Journal of Ocean Engineering and Technology, Vol. 16, No. 6, pp. 25-31.
[14] Natesan, Arun K1994. “Kinematic analysis and synthesis of Four-bar mechanisms for straight line coupler curves”, Dissertation. Rochester Institute of Technology.
[15] Ohtsu, K, Shoji, K and Okazaki, T(1996), ““MINIMUM - TIME MANEUVERING OF A SHIP, WITH WIND DISTURBANCES”, Control Eng. Practice”, Vol. 4, No. 3, pp. 385-392.

[16] Purcell, M and et al(2000), “New capabilities of the REMUS autonomous underwater vehicle”, Proceedings MTS/IEEE Oceans 2000, Providence. Rhode Island.

[17] Park, JY and et al(2015), ““Study on Coning Motion Test for Submerged Body””, Journal of Ocean Engineering and Technology, Vol. 29, No. 6, pp. 436-444.

[18] Park, JY and et al(2020), ““Study on the Estimatino of Autonomous Underwater Vehicle’s Maneuverability Using Vertical Planar Motion Mechanism Test in Self-Propelled Condition””, Journal of the Society of Naval Architects of Korea, Vol. 57, No. 5, pp. 287-296.

[19] SNAME(1950), ““Nomenclature for Treating the Motion of a Submerged Body Through a Fluid”. The Society of Naval Architects and Marine Engineerings”, Technical and Research Bulletin, No. 1-5, pp. 1-15.
[20] Watt, GD(2007), ““Modelling and Simulating Unsteady Six Degrees-of-freedom Submarine Rising Maneuvers””, DRDC Atlantic TR, pp. 2007-008.
- TOOLS
-
METRICS

-
- 0 Crossref
- 0 Scopus
- 2,262 View
- 36 Download
- Related articles
-
Development of Safety Index for Evaluation of Ship Navigation2014 June;38(3)
Development of the Rudder Roll Control System of a Vessel in Irregular Waves2005 December;29(10)
Development of Analysis Module for Marine Traffic Information Using PC Camera2005 June;29(4)
Development of a GUI Program for the Position Prediction of Distressed Vessel2002 December;26(5)













 PDF Links
PDF Links PubReader
PubReader ePub Link
ePub Link Full text via DOI
Full text via DOI Download Citation
Download Citation Print
Print