Analysis on Hydrodynamic Force Acting on a Catamaran at Low Speed Using RANS Numerical Method
Article information
Abstract
This paper discusses the hydrodynamic characteristics of a catamaran at low speed. In this study, the Delft 372 catamaran model was selected as the target hull to analyze the hydrodynamic characteristics by using the RANS (Reynold-Averaged Navier-Stokes) numerical method. First, the turbulence study and mesh independent study were conducted to select the appropriate method for numerical calculation. The numerical method for the CFD (Computational Fluid Dynamic) calculation was verified by comparing the hydrodynamic force with that obtained experimentally at high speed condition and it rendered a good agreement. Second, the virtual captive model test for a catamaran at low speed was conducted using the verified method. The drift test with drift angle 0-180 degrees was performed and the resulting hydrodynamic forces were compared with the trends of other ship types. Also, the pure rotating test and yaw rotating test proposed by Takashina, (1986) were conducted. The Fourier coefficients obtained from the measured hydrodynamic force were compared with those of other ship types. Conversely, pure sway test and pure yaw test also were simulated to obtain added mass coefficients. By analyzing these results, the hydrodynamic coefficients of the catamaran at low speed were estimated. Finally, the maneuvering simulation in low speed conditions was performed by using the estimated hydrodynamic coefficients.
1. Introduction
Nowadays, catamaran is widely used for variety of purposes due to their excellent performance in terms of safety, resistance performance, transverse stability, and large deck area. The catamaran not only operates at high speed, but it also operates at low speed in special cases such as near harbor. A large number of theoretical and numerical studies as well as experimental investigations have recently been conducted with a focus on the hydrodynamic force acting on the catamaran. For example, Zlatev et al.(2009) performed an experiment involving a high-speed catamaran at Bulgarian Ship Hydrodynamic Center (BSHC) to investigate the maneuvering characteristics at various water depth ratios and different Froude numbers. The results showed that the hydrodynamic force increases with decreasing water depth and increasing Froude number. Milanov et al.(2012) conducted an experiment on a Delft 372 catamaran with the water-jet in both deep and shallow waters. The hydrodynamic coefficients were estimated to predict the maneuverability, and then the mathematical model for the water-jet of Delft 372 catamaran was established. Other studies have also investigated the seakeeping performance (Castiglione et al., 2011), resistance performance, and interaction between demi-hulls (Broglia et al., 2011) for Delft 372 catamaran at high speed. However, the low speed movement of the catamaran near the harbor has yet to be studied.
The ship operates at low speed in such a situation to move slowly and avoid the obstacle. Takashina (1986) proposed the pure rotating test and the yaw rotating test to calculate hydrodynamic coefficients for tugboat at low speed and large drift angle. Fourier series was applied to estimate hydrodynamic coefficients, and a mathematical model is established for ship at low speed condition. In a different study, Umeda et al.(1989) investigated cross flow force and lateral force through a circular motion test of the trawler at low speed and large drift angle. A mathematical model was developed for validation for both a longitudinal symmetric ship and a non-symmetric ship. In addition, Oh et al.(2012) presented a number of models for ship maneuvering at low speed proposed by other researchers. A comparison among the models for various types of ship is implemented to help accurately predict the hydrodynamic force of any given ship in low speed.
Regarding the use of CFD-based simulation to estimate hydrodynamic characteristics, Hajivand et al.(2015) have performed a virtual captive model test for DTMB 5512 using RANS (Reynolds-Averaged Navier-Stokes) numerical method based on STAR-CCM+ to estimate the hydrodynamic characteristics. OpenFOAM software has also been used to predict hydrodynamic characteristics for KCS by Islam et al.(2018). In addition, Liu et al.(2018) conducted a virtual captive model test for KCS (KRISO Container Ship) by using unsteady RANS to predict linear and nonlinear hydrodynamic coefficients in the 3rd-order Abkowiz model. The uncertainty analysis for GCI (Grid Convergence Index) and time step is conducted for dynamic testing, and the standard turning and zigzag maneuvers are predicted by using the estimated hydrodynamic coefficients. The conditions used in these studies included a conventional ship and a small or moderate drift angle.
This paper focuses on estimating the hydrodynamic force acting on Delft 372 catamaran operating at low speed by using RANS-based solver in Ansys FLUENT 17.2. A verification is performed for RANS-based method with the turbulence study and mesh independence study to select the most appropriate method. A virtual captive model test is simulated to predict hydrodynamic force at low speed. Especially, large drift angle is performed in the static drift test, pure rotating test, and yaw rotating test at low speed. Fourier approximation is applied to estimate hydrodynamic coefficients by analyzing the calculated hydrodynamic force. The trajectory of the catamaran at low speed is predicted using estimated hydrodynamic coefficient.
2. Theory Background
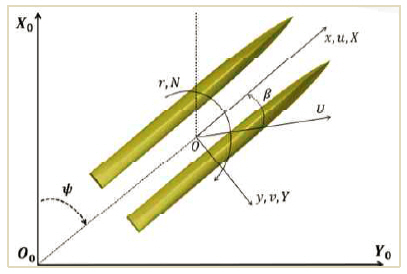
2.1 Coordinate system
Two coordinate systems are used to define the kinematic and hydrodynamic forces acting on the Delft 372 catamaran. Fig. 1 shows the earth-fixed coordinate system Ox0y0 that is set to be fixed with origin and the body-fixed coordinate system Oxy that is fixed with the ship hull. Both the coordinate systems follow the right-hand rule, which means that the vertical axes are pointing downward and the lateral axes are pointing to the right-hand side. The origin of body-fixed coordinate system is located at the midship and its x-axis is directed to ship bow. The motion equation for a surface ship in a horizontal plane is as follows,
where m is the ship mass, u, υ and r are the surge velocity, sway velocity, and yaw rate, respectively. In addition,
2.2 Governing equation
In this study, the flow around the ship is assumed to be incompressible. The continuity equation and Navier-Stokes equation are chosen as governing equations:
where ui and uj are the average velocity components;
2.3 Dimensionless quantity
The obtained force and moment from simulation are non-dimensionalized by length (L), draft (T), and speed. The non-dimensionless force, moment, and motion are given as follows,
2.4 CFD-Based modeling
2.4.1 Numerical modeling
The rectangular domain covering the catamaran is generated to simulate the virtual captive model test. The computational domain is selected to be sufficiently large to avoid backflow and side flow at a high drift angle. In the static test, the dimension of the rectangular is 7L in length, 4L in width, and 2.5L in height. The rectangular is also covered for the inner domain. In the dynamic test, the dimensions are 6L, 4L, and 2.5L for the length, width, and height of the rectangular, respectively. The inner domain is covered a cylinder with a radius of 2.5 m and a height of 1 m to avoid mesh failure at sharp corners. In addition, a physical condition is applied to the boundaries domain. The inlet boundary condition upstream is taken as a pressure-inlet with an open channel; the outlet condition downstream is taken as a pressure-outlet with an open channel. A no-slip wall is set for the hull face and symmetry is assigned for the top face, bottom face, and side faces. The Volume of Fluid is applied to model the two-phase volume of the fluid technique. The fluid domain is discretized into a tetrahedral unstructured mesh in the inner domain of the static test and the whole domain of dynamic test. Furthermore, a hexahedron structured with multi-block is generated in the outer domain of the static test in order to reduce the number of elements. Because the wall function is applied to improve the accuracy of the flow resolution, prism layer mesh is used near the hull surface to resolve the boundary layer flow. The y+ value of 30 is estimated for Reynolds number of 9.7E+5. The mesh generation for the static test and the dynamic test is shown in Fig. 2.
According to Practical Guidelines for ship CFD Application (ITTC, 2011), a two-equation turbulence model is used to enable an accurate prediction of the ship dynamic. The turbulence models of k-ε Realizable and k-ω SST (Shear Stress Transport) are employed in the calculation. In addition, the SIMPLE (Semi-implicit Method for Pressure Link Equations) algorithm is applied to obtain the pressure and velocity field. The quantities at the cell faces are calculated from the cell centered values using the second order upwind method.
2.4.2 Numerical analysis
Before proceeding with the computation, it is necessary to first perform a verification study. Thus, the turbulence study and mesh independence study are conducted to select the most appropriate method for this study. Experimental results obtained from the BSHC (Bulgarian Ship Hydrodynamic Center) are used for verification in the present study.
In the turbulence study, two turbulence models of k-ε Realizable and k-ω SST are evaluated initially. A drift test case of 6 degrees is carried out at the Froude number of 0.3 for two turbulence model to obtain the hydrodynamic force.
For the mesh independence study, three different grid size are used and the corresponding forces are evaluated in a drift test with a drift angle of 6 degrees at Froude number 0.3. The grid refinement is achieved by applying a refinement factor
where
2.5 Captive model test
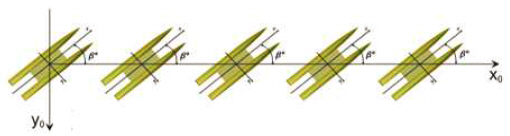
2.5.1 Static drift test
The ship is towed at a constant speed with a constant drift angle ranging from zero to 180 degrees. Fig. 3 shows a schematic of this motion.
Fourier approximation is used in deriving the hydrodynamic coefficients. The following expression using Fourier series is expressed as follows,
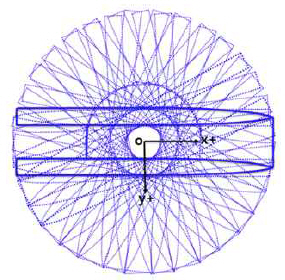
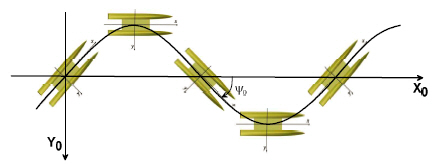
2.5.2 Pure rotating test
The test is conducted with a ship speed of zero while rotating around a vertical axis through the center of gravity of the ship with a constant yaw rate, as shown in Fig. 4. The hydrodynamic force in the pure rotating test is given in Eq. (9) as:
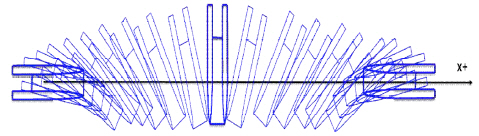
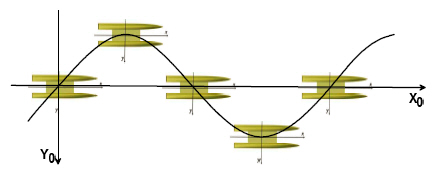
2.5.3 Yaw rotating test
As shown in Fig. 5, the ship is simulated to rotate around the vertical axis through the center of gravity at a constant speed and a constant yaw rate. The motion given to the ship during the yaw rotating test with a large drift angle can be described as follows,
The hydrodynamic force for the drift angle measured between zero degrees and 360 degrees is described as the sine and cosine functions. Thus, the hydrodynamic force can be expressed in terms of Fourier approximation with respect to the drift angle in Eq. (11). On the other hand, the variations of these coefficients are supposed as shown in Eq. (12).
By substituting Eq. (12) into Eq. (11), X’, Y’ and N’ can be expressed as shown in Eqs. (13)-(15), respectively.
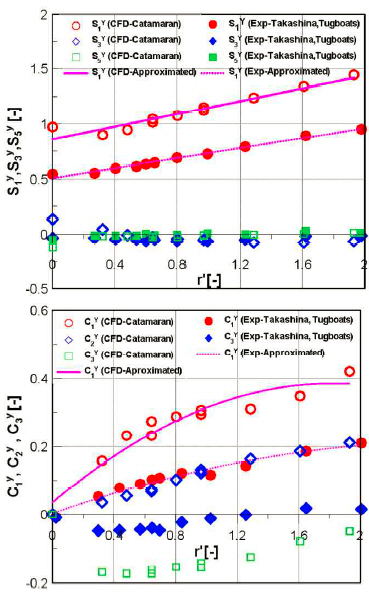
On the other hand, the terms of the Fourier coefficients can be transformed into conventional expressions with hydrodynamic coefficients according to the relationship between β and u, and v based on trigonometry. According to the mathematical model proposed by Takashina (1986), the hydrodynamic equations for X’, Y’, and N’ are respectively expressed as follows,
Finally, the hydrodynamic coefficients for X’, Y’, and N’ can be respectively obtained from the following relationships shown in Eqs. (19)∼(21).
It should be noted that
2.5.4 Harmonic test
The ship is simulated to oscillate in a sinusoidal motion at a constant speed and a constant frequency. The pure sway test and the pure yaw test are achieved in this study. The main reason these tests are performed is to estimate the added mass coefficients with v oscillating harmonically in the pure sway test and the coefficients relative to the yaw rate with harmonic oscillating yaw motion in the pure yaw test. The motions of the pure sway test and the pure yaw test is described in Eqs. (22) and (23), respectively. Figs. 6~7 show the definitions of the pure sway test and the pure yaw test, respectively.
The mathematical models for the harmonic test (Hajivand et. al., 2015 and Liu et. al., 2018) are shown in Eqs. (24) and (25) for pure sway test and pure yaw test, respectively.
Fourier approximation for the harmonic test is adopted to derive the hydrodynamic coefficients. The harmonic forms of the pure sway test and the pure yaw test are achieved by substituting the motion into the mathematical model as presented in Eqs. (26) and (27) for pure sway and pure yaw, respectively.
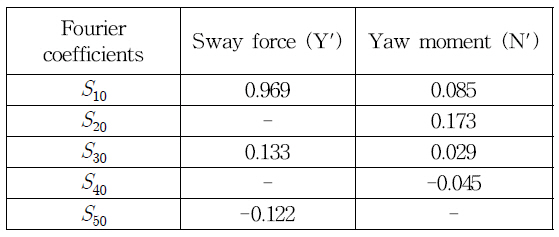
The Fourier sine and cosine coefficients in these expressions are given in Table 1. The functions of the N component are not listed in the table since they are the same as those of the Y component, and it can be obtained by replacing "Y" with "N".
3. Results
3.1 Case study
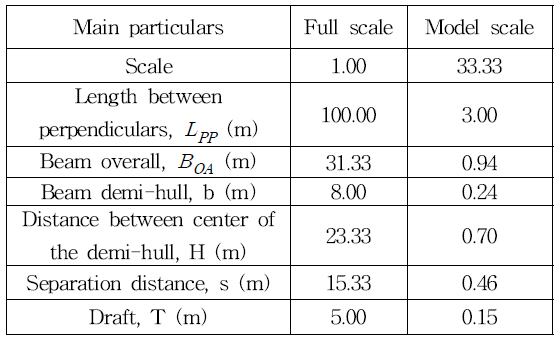
The target ship in this study is the Delft 372 catamaran model that originally used in TU-Delft by Vant Veer (1988). Main parameters of the catamaran are listed in Table 2. Fig. 16 shows the 3D model of Delft 372 catamaran.
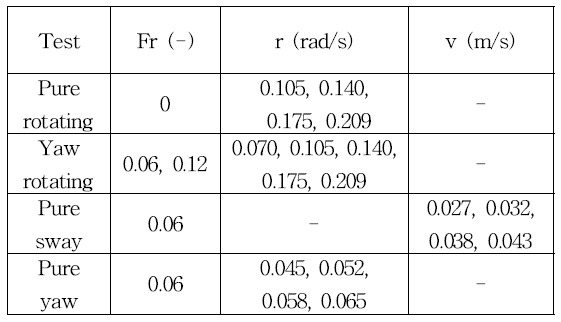
The computational conditions are depicted in Table 3 for static test and Table 4 for dynamic test.
3.2 CFD verification
3.2.1 Turbulence study
Fig. 9 shows the comparison of the turbulence study results. It can be seen that both of the turbulence models predict the hydrodynamic force of the catamaran with good accuracy. However, the results of the k-ω SST turbulence model are slightly better than those of the other two.
3.2.2 Mesh independence study
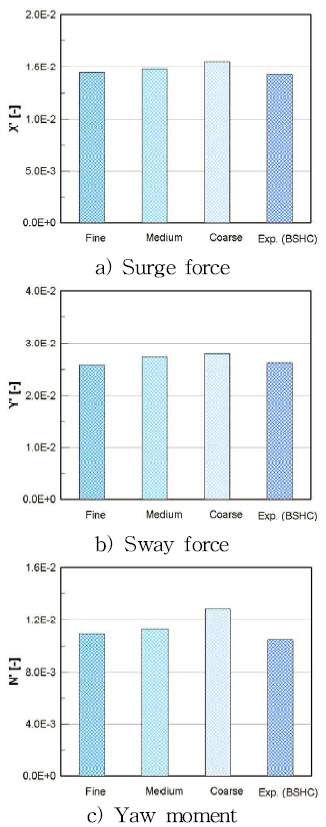
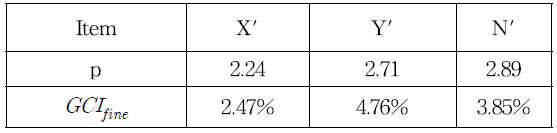
The three densities of the fine grid, the medium grid, and the coarse grid are counted to be approximately 6.77M, 4.90M, and 3.55M, respectively. The mesh independence study is performed with the k-ω SST turbulence model. Table 5 shows the solution of the mesh convergence study. In addition, the computation results obtained from the different mesh sizes are shown in Fig. 10. It indicates that the error of the solution is reduced as the generated grid becomes finer.
3.2.3 Verification
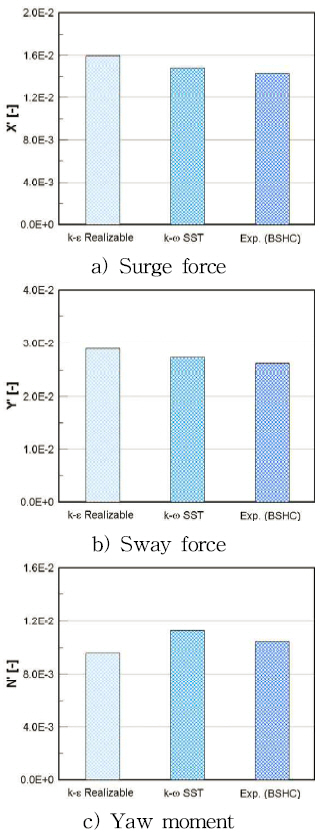
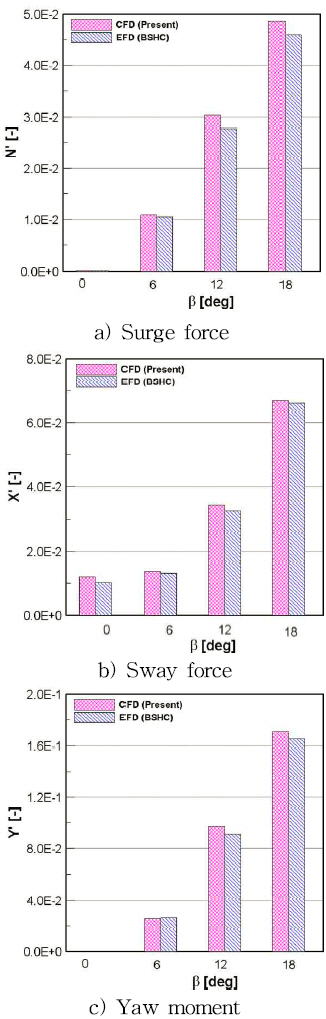
The verification is simulated for a fine grid with the k-ω SST turbulence model at a Froude number of 0.3 in the case of the drift test. In Fig. 11, the calculated hydrodynamic force is compared with the experimental results from BSHC. It can be seen that the hydrodynamic force of computation results are consistent with the experimental results. Therefore, fine grid and k-ω SST are simulated in further study.
3.3 Results of virtual captive model test
3.3.1 Static drift test
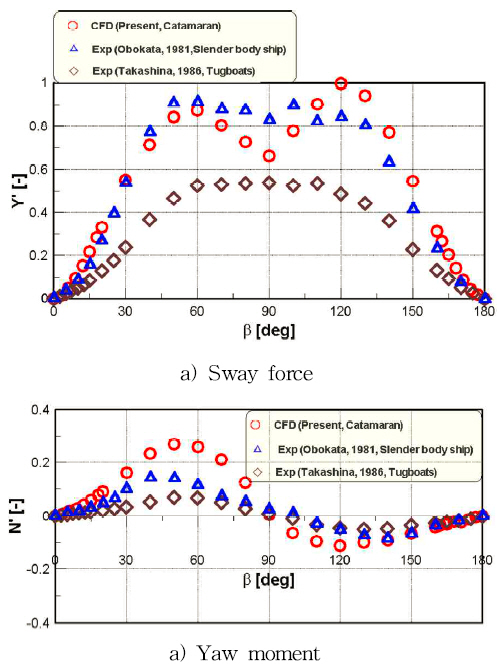
The hydrodynamic forces of the static drift test for drift angles ranging from zero to 180 degrees at low speed are shown in Fig. 12. The comparison with other ship types shows that the trend of the hydrodynamic force in the present study is consistent with the trends of the experimental results of the other ship types. However, the difference among results due to the different ship types is observed, especially tugboats. Furthermore, slender shape of a catamaran and slender body ship gives a similar results.
By approximating the measured data, the Fourier coefficients are obtained by using Eq. (8) and presented in Table 6.
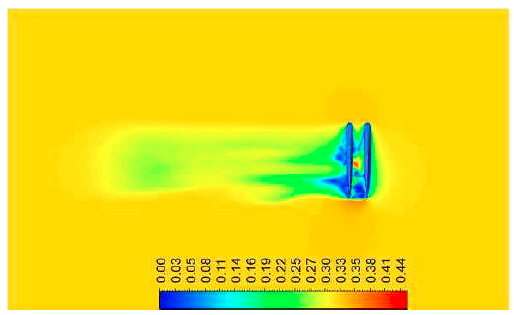
Furthermore, the below figure shows the velocity contour of static drift test at 90 degrees. It can be seen that the velocity between two side faces where symmetry condition is set. It is nearly same value with inlet velocity despite of low speed condition. Since velocity changes occur around the ship, applying symmetry conditions seems appropriate.
3.3.2 Pure rotating test
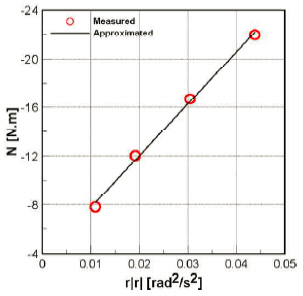
Fig. 14 shows the yaw moment acting on the catamaran against the yaw rate squared r|r|. The hydrodynamic coefficient N’r|r| can be obtained based on the ratio of yaw moment to yaw rate squared.
3.3.3 Yaw rotating test
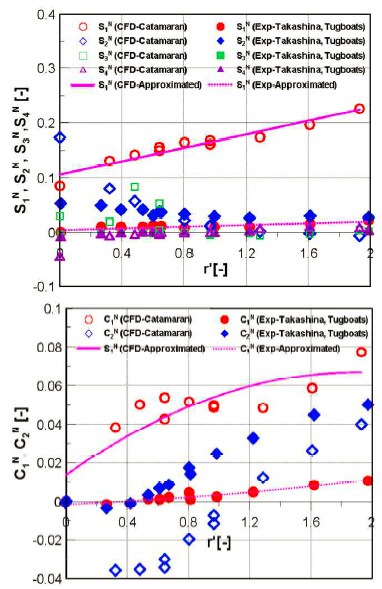
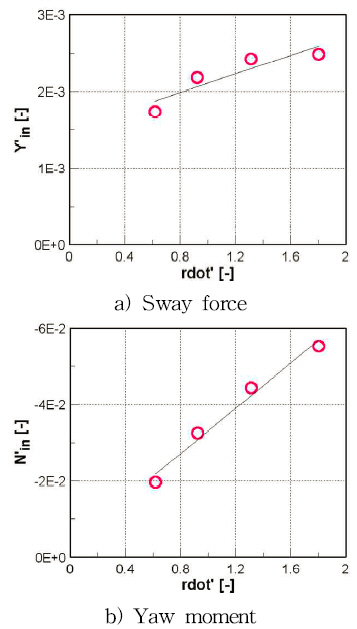
The Fourier coefficients obtained from yaw rotating test are plotted against the non-dimensional yaw rates in Figs. 15~17 for X’, Y’, and N’, respectively. In addition, the trends of the Fourier coefficients of catamaran are compared with those of the Fourier coefficients of tugboats obtained by Takashina(1986). It can be observed that Fourier coefficients of the tugboats are smaller than the catamaran results due to the smaller values of hydrodynamic forces of the tugboats as shown in Fig. 12. Nevertheless, the similar trends between tugboats and catamaran can illustrate that the obtained coefficients of catamaran are appropriate results.
3.3.4 Harmonic test
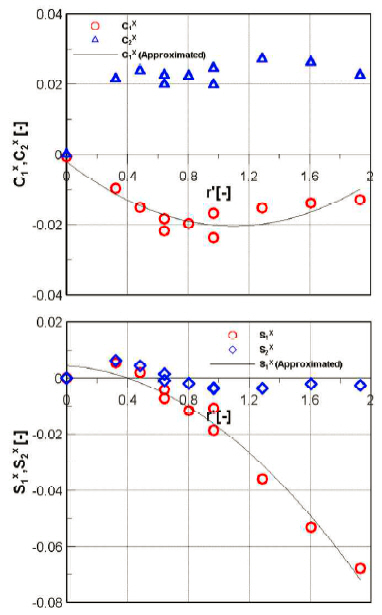
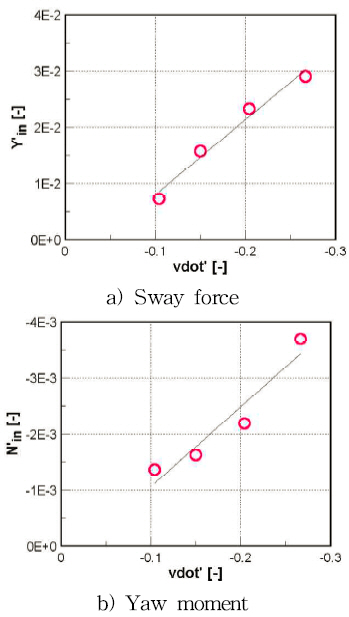
The Fourier coefficients obtained from the harmonic test for in-phase components are drawn versus lateral acceleration in Fig. 18 for the pure sway test and versus yaw rate in Fig. 19 for the pure yaw test. By fitting the in-phase components, the added mass coefficients can be estimated.
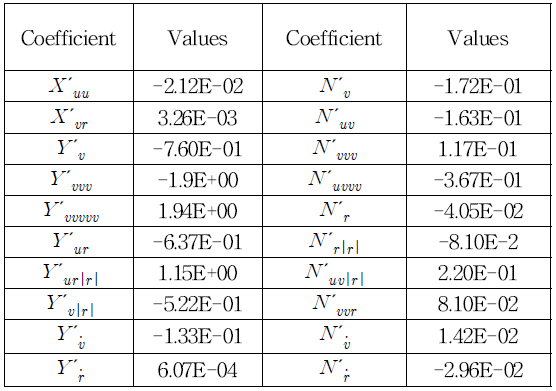
Finally, the hydrodynamic coefficients of a Delft 372 catamaran operating at low speed are estimated using the virtual captive model test and the results are presented in Table 7.
3.3.5 Maneuvering simulation
The water-jet propulsion is used as propulsor device and steering device. Thus, the right-hand side of Eq. (1) is expressed as
subscript H and WJ indicate hull and water-jet, respectively.
A experiment for Delft 372 catamaran with water-jet propulsion was performed by Milanov, et al., (2012) in order to obtained mathematical model and hydrodynamic coefficients of water-jet as shown in Table 8.

Hydrodynamic coefficients of water-jet (Milanov, et al., 2012)
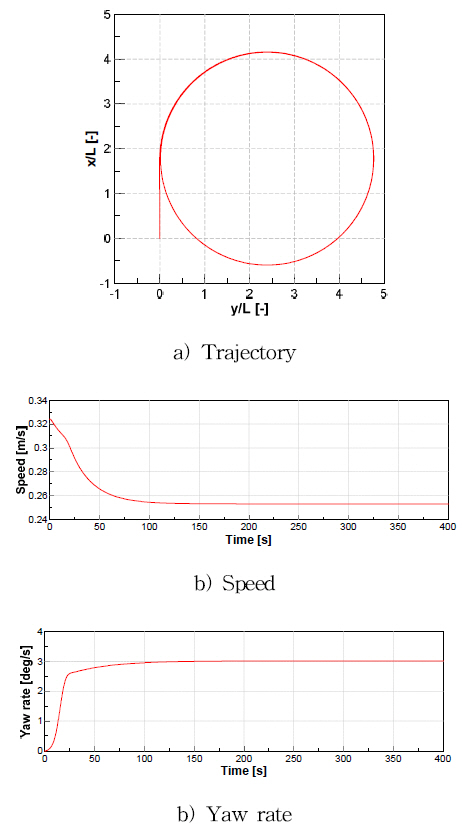
Fig. 20 shows the simulation result of turning circle maneuvers at low speed when the water-jet impeller RPM is kept to be constant and water-jet nozzle deflection is 35 degrees. The trajectory is described for the turning path. The speed and yaw rate are changing throughout turning circle simulation.
4. Conclusion
In this study, the virtual captive model test had been implemented using the CFD-based method. Ansys FLUENT version 17.2 was used to simulate the fluid flow through the Delft 372 catamaran. The hydrodynamic force acting on the catamaran at low speed and high drift angle is also estimated.
The results verified that the RANS-based method provided an accurate prediction of the catamaran. The k-ω SST turbulence model and fine mesh were consistent with the experiment results in the case of a drift test at high speed.
CFD simulations were performed for the static drift test, the pure rotating test, the yaw rotating test, and the harmonic test. In particularly, the coupling coefficients for a catamaran at low speed were estimated by performing the pure rotating test and the yaw rotating test. The Fourier approximation provides an accurate prediction of the hydrodynamic coefficients. On the other hand, the obtained hydrodynamic force could be approximated well by the linear reaction with sway velocity, but the added mass coefficients were not fitted very well to the force and moment in the harmonic test. In total, 20 maneuvering coefficients were estimated.
The estimated hydrodynamic coefficients was used to evaluate the catamaran's turning ability at low speed.
Acknowledgements
This work was supported by a grant-in-aid of HANWHA SYSTEMS.