부산 북항 통항 선박간의 시간간격 최적 확률분포에 관한 연구
A Study on the Optimal Probability Distribution for the Time Interval Between Ships on the Traffic Route of the Busan North Port
Article information
Abstract
항로는 선박의 통항이 빈번하고 특히, 항로의 입구부는 선박의 출입이 잦아 사고의 위험이 높은 지역이지만, 항로 단면에서의 통항 분포에만 초점을 맞춘 연구가 다수였으며, 항로 통항 선박간의 시간분포에 대한 연구는 부족하였다. 이에 본 연구에서는 대상항로에서의 통항 선박간의 시간 최적분포를 분석하기 위해서 1주일간의 선박의 통항현황을 조사하였다. 통항현황을 바탕으로 항로 입구부에 1개의 Gate line을 선정하고, Gate line을 통과하는 선박을 입출항, 교통량으로 구분하여 분석하였다. 대상항로의 해상교통 분석 자료를 바탕으로 입출항과 교통 량으로 구분하여 항로 통항 선박간의 시간 최적 확률분포를 분석하였다. 최적 확률분포를 분석하기 위하여 경계분포, 비경계분포, 비음수분포, 고급분포로 구분하여 총 31개의 확률분포를 적용하였으며, 최적 확률분포 상위 3개를 분석하기 위하여 KS 검정을 사용하였다. 분석 결과 대상 항로에서 통항 선박간의 최적 시간 확률분포는 Wakeby 분포로 분석되었으며, 도로교통 등의 선행연구에서 사용한 비음수 분포와 다르게 고 급분포가 대부분을 차지하는 것으로 분석되었다. 따라서 향후 항로 통항 선박간의 시간 분포를 적용함에 있어 다른 교통 분야의 선행연구에서 사용한 대표적인 확률분포를 적용하는 것은 적합하지 않는 것으로 판단된다. 또한 실제 교통조사 시 통항 선박간의 거리와 최적 확률분포로 추정한 거리가 비교적 유사함을 확인하였다. 다만 본 연구는 대표적인 1개의 항로를 분석한 만큼 향후 다양한 항로에서의 통항 선박간의 시간 간격 및 교통용량 산정 등의 후속연구가 필요한 것으로 판단된다.
Trans Abstract
Traffic routes typically have heavy traffic. Especially, the entrance of the route has a high risk of accidents occurring because of ships entering and exiting the port. However, almost of studies have focused on the distribution of traffic on the route. Thus, studies on the distribution between ships for passing through the route are insufficient. The purpose of this study was to analysis the traffic in the Busan north port No.1 route for one week. Based on present traffic conditions, one gate line was settled on the route with an analysis of traffic conditions. Based on the analysis data, each optimal time probability distribution between ships was divided into inbound/outbound and traffic volume. An analysis of the optimal probability distribution, was applied to 31 probability distributions divided into bounded, unbounded, non-negative, and advanced probability distribution. The KS test was applied for identifying three major optimal time probability distributions. According to the KS test results, the Wakeby distribution is the best optimal time probability distribution on the designated route. Although the optimal time probability distribution for other transportation studies such as on vehicles on highways is a non-negative probability distribution, this distribution is an advanced probability distribution. Thus, the application of major probability distribution for using other transportation studies is not applicable to this study Additionally, the distance between ships in actual traffic surveys and the distance estimated by the optimal probability distribution were compared. As a result of the comparison, those distances were fairly similar. However, this study was conducted in only one major port. Thus, it is necessary to investigate the time between ships and calculate a traffic volume on varying routes in future studies.
1. 서 론
항로는 선박이 통항하는 통로로서 선박의 통항이 빈번한 곳 이다. 특히 항로의 입구부는 다른 장소보다 선박의 출입이 꾸 준히 일어나는 곳이므로 해양사고의 발생확률이 보다 높다. 따라서 항로에서의 선박 통항 흐름과 교통용량 수준을 측정하 는 것이 필수적이며, 일찍이 많은 연구들이 수행되어왔다.
선행연구에서는 항로 폭을 기준으로 항로 단면에서의 선박의 최적 통항 확률분포를 분석하거나 이를 기반으로 항로에서의 통 항 안전성을 분석하는 연구가 주를 이루었다. 예를 들어 Kim and Song(2014)는 AIS(Automatic Identification System, 이하 AIS) 데이터를 이용하여 부산, 울산, 마산항의 진·출입 항로 단면 에서의 통항 선박 최적 확률분포를 구하였고, Kwon(2015)은 인 천대교와 목포대교의 주 교각 사이를 통항하는 선박의 확률분포 의 정규성을 검증하였다. 특히, 항로 단면에서의 선박의 최적 통 항 확률분포는 Yang et al.(2004)와 같은 다수의 연구 및 해상교 통안전진단에서 선박의 통항 안전성 평가를 위해 널리 사용되어 왔다.
하지만 근래에 들어 항로 단면에서의 연구를 벗어나 선박의 통항 간격에 대한 연구도 수행되었다. Lee et al.(2015)과 Shin(2018)은 인천항 도선점 부근의 선박 간섭확률을 분석하 기 위하여 푸아송 분포를 이용하여 단위 시간당 대상 구간을 통과할 확률을 구하고 이를 바탕으로 교행확률을 분석하였다.
다만, 앞서 설명한 선행연구에서는 항로 단면에서의 통항분 포에만 초점을 맞춘 연구가 다수였으며, 단위 시간 당 대상 구 간 통과 확률을 구하는 정도였으며, 선박 통항 흐름과 교통용 량의 수준을 측정하기 위한 연구는 부족하다는 한계가 있었다.
이에 본 연구에서는 항로 통항 선박간의 시간 최적 분포를 분석하기 위하여 선박의 교통현황을 조사하고, 교통량을 기준 으로 구분하였으며, 항로 통항 선박간의 시간 최적 확률 분포 를 구하였다.
2. 최적 확률분포의 선정
2.1 확률분포 모형의 선정
선행연구에서 항로에서의 선박 항행패턴을 분석하기 위하 여 가장 많이 사용하는 방법으로 항로상의 최적 확률분포의 형태를 파악하는 방법이 널리 사용되었다. 확률분포는 확률변 수의 분포를 함수로 나타낸 것으로 연속확률변수 x에 대하여 식(1)이 성립된다.
여기서 f(x)는 연속확률변수 x의 확률분포라고 한다.
본 연구에서는 가장 많이 사용하는 단일 확률분포를 이용하 였고, 크게 경계분포(Bounded distribution), 비경계 분포 (Unbounded distribution), 비음수분포(Non negative distribution)과 고급분포(Advanced distribution) 등으로 구분 하였다.
2.1.1 경계분포(Bounded distribution)
연속확률분포의 구간이 [a, b]로 한정되는 함수로서 본 연구 에서는 베타분포(Beta distribution), 존슨에스비분포(Johnson SB distribution), 균일분포(Uniform distribution), 퍼트분포(Pert distribution), 검출력함수 분포(Power Function distribution)를 사용하였다.
본 연구에서 사용한 경계분포 중 베타분포의 확률밀도함수 는 식(2)와 같고, 확률분포의 모형은 Fig.1과 같다.
여기서 α1과 α2는 연속 형태 매개변수로서, 모두 0보다 크고, a와 b는 연속 경계 매개변수로서 a < b이다.
2.1.2 비경계분포(Unbounded distribution)
연속확률분포의 구간이 [-∞,∞]인 함수로서 본 연구에서는 코쉬분포(Cauchy distribution), 오차분포(Error distribution), 검벨최소분포(Gumbell Min. distribution), 존스에스유분포 (Johnson SU distribution), 라플라스분포(Laplace distribution), 로지스틱분포(Logistic distribution), 정상분포(Normal distribution) 를 사용하였다.
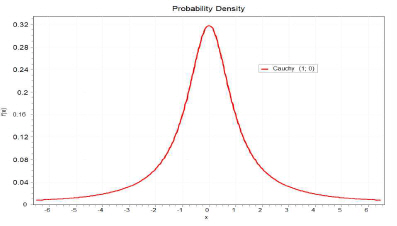
본 연구에서 사용한 비경계분포 중 코쉬분포의 확률밀도함 수는 식(3)과 같고, 확률분포의 모형은 Fig.2와 같다.
여기서 σ는 연속 척도 매개변수로 0보다 큰 값이며, μ는 연 속 위치 매개변수이다.
2.1.3 비음수분포(Non negative distribution)
대부분의 비음수분포는 식(4)와 같이 정의할 수 있다.
여기서 γ 는 연속 위치 매개변수이다.
비음수분포는 매개변수 γ를 고정값 0으로 설정하면 단순화 가 가능하고, 이렇게 단순화한 분포를 이용하여 많은 부분에 사용하고 있다. 하지만 경우에 따라서 매개변수를 0이 아닌 값 으로 사용하면 더 유효한 모델을 개발할 수 있다. 따라서 비음 수분포는 모든 매개변수를 활용하는 형태와 단순화된 형태로 나눌 수 있다.
본 연구에서는 매개변수를 모두 활용하는 형태로 분석하였으 며, 버분포(Burr distribution), 다금분포(Dagum distribution), 얼 랑분포(Erlang distribution), 피로수명분포(Fatigue life distribution), 프레셰분포(Frechet distribution), 감마분포(Gamma distribution), 일반화감마분포(Generalized gamma distribution), 역가우시안분포 (Inverse gaussian distribution), 로그감마분포(Log-gamma distribution), 로그로지스틱분포(Log-logistic distribution), 로그정규분포(Log -normal distribution), 와이블분포(Weibull distribution) 피어슨 -Ⅴ분포(Pearson-5 distribution), 피어슨-Ⅵ분포(Pearson-6 distribution) 를사용하였다.
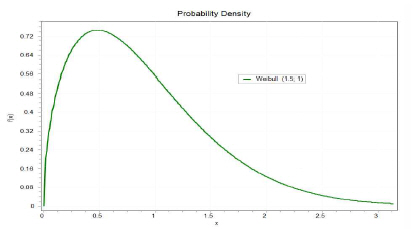
본 연구에서 사용한 비음수분포 중 와이블분포의 확률밀도 함수는 식(5)와 같고, 확률분포의 모형은 Fig.3과 같다.
여기서 α는 연속 형태 매개변수, β는 연속 척도 매개변수로 모두 0보다 크고, γ는 연속 위치 매개변수이다.
2.1.4 고급분포(Advanced distribution)
연속분포 분류 정의 범주에 속하지 않은 분포가 있을 수 있 으며, 이러한 분포가 더 유효한 모델일 수 있다. 이러한 분포 를 고급분포라고 하며 본 연구에서는 일반화극치분포 (Generalized Extreme Value Distribution),일반화로지스틱분포 (Generalized Logistic Distribution), 일반화파레토분포(Generalized Pareto Distribution), 로그피어슨-Ⅲ분포(Log-pearson 3 Distribution), 웨이크비분포(Wakeby Distribution)를 사용하였다.
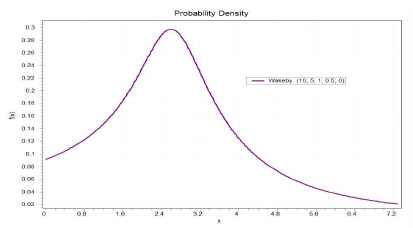
본 연구에서 사용한 고급분포 중 웨이크비분포의 확률밀도 함수는 식(6)과 같고, 확률분포의 모형은 Fig.4와 같다.
여기서 α , β, γ, δ, ζ는 연속 매개변수이다.
2.2 최적 분포의 선정
선정된 확률분포 모형 중 어느 분포가 항로에서의 선박 시 간 분포를 가장 잘 나타내는지를 결정하기 위하여 확률분포의 적합성 검증(Goodness of Fit)을 통하여 최적 분포를 선정하 였다. 적합성 검정에는 일반적으로 카이제곱, 콜로고르프 스미 노프(Kolmogorov Smirnov, 이하 KS), 앤더슨 달링 검정이 있 지만 본 연구에서는 KS 검정을 통해 최적 분포를 선정하였다.
KS 검정은 가정한 확률분포의 누적분포함수와 표본 데이터 의 경험적 누적분포함수를 비교하여 검정하는 것으로 모든 변 수의 범위에 있어 경험적 누적분포함수와 가정한 확률분포함 수사이의 절댓값 차이가 가장 큰 것을 찾는 방법으로 식(7)과 같다.
여기서, Dn은 KS 값을, Fn은 경험적 누적분포함수를, F은 가정한 확률분포의 누적분포함수를 의미한다.
Dn이 유의수준 α로 가정한 KS 임계치보다 크면 유의수준 α에서 기각된다.
KS 검정은 카이제곱 검정과 달리 원래의 빈도수를 그대로 사용할 수 있으며, Dn의 값이 작을수록 가정한 확률분포가 데 이터에 잘 적합하다는 것을 의미한다.
3. 항로 통항 선박간의 시간 최적 분포 분석
3.1 대상 항로의 선정 및 통항 자료 수집
항로를 통항하는 선박간의 시간을 분석하기 위해서는 먼저 해상교통조사를 시행하여야 한다. Yoo et al.(2015)는 해상교 통조사를 시행할 경우 요일 변화지수를 고려하여 최소 1주일 실시하면 최대 표준오차를 21.6% 이내로 산출할 수 있다고 하 였다.
이에 본 연구에서는 오륙도 방파제부터 부산항대교에 이르 는 부산항 북항 제1항로를 대상항로로 선정하였으며, Fig 5와 같이 출·입항하기 위해 교통이 밀집되는 대상항로의 입구부분 인 조도 방파제와 오륙도 방파제 사이의 구역에 목표선을 설 정하였다.
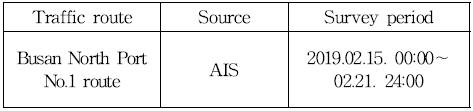
Table 1과 같이 대상항로의 교통조사는 요일 변화지수를 고려하기 위해 2019년 2월 15일 00시부터 2월 21일 24시까지 연속된 1주일동안 시행하였으며, AIS를 이용하여 현장 수집하 였다.
3.2 대상항로 통항 현황 분석
대상항로의 목표선에서의 통항 선박간의 시간 분포를 분석 하기 위하여 1주일간의 교통조사 자료를 분석하였다.
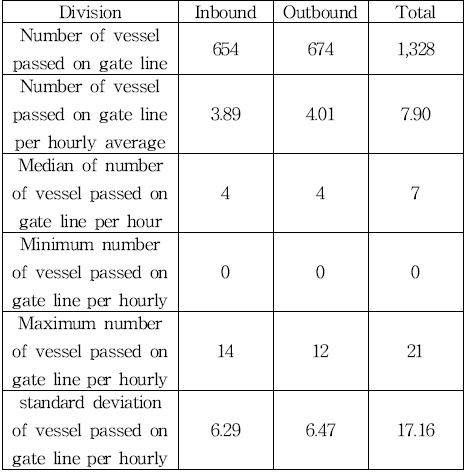
Table 2와 같이 교통조사 기간 동안 입항한 선박은 654척 (시간당 평균 3.89척), 출항한 선박은 674척(시간당 평균 4.01 척), 총 1,328척(시간당 평균 7.90척)의 선박이 목표선을 통과 하였다. 교통조사 기간 동안 한 척도 목표선을 통과하지 않은 시간대가 존재하였으며, 입항은 최대 14척, 출항은 최대 12척, 총 최대 21척의 선박이 목표선을 통과하였다.
Fig. 6과 표준편차의 통계치에서 보는 바와 같이 입항과 출 항 선박 수의 변화의 폭이 큰 차이 없이 유사함을 알 수 있다.
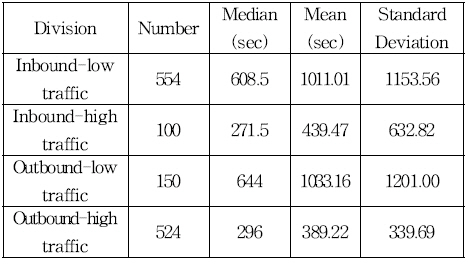
Jeong(2016)은 자전거교통류의 차두시간 분포모형을 적용 하기 위해 교통량에 따라 구분하였다. 이는 교통량이 적으면 평균과 표준편차가 커지게 되고, 교통량이 많아지면 평균과 표준편차가 작아지는 특성을 구분하여 설명하기 위함이다. 따 라서 본 연구에서도 대상항로에서의 해상교통류를 낮은 교통 량과 높은 교통량으로 구분하였다. 교통량의 기준은 Jeong(2016)의 연구에서와 같이 총 통항선박의 중간 값인 7척, 평균값이 7.9척임을 감안하여, 시간당 7척 이하를 낮은 교통량 으로 하고 8척 이상을 높은 교통량으로 구분하여 분석하였다.
Table 3과 같이 입항시 낮은 교통량은 554척, 높은 교통량 은 100척이었으며, 출항시 낮은 교통량은 534척, 높은 교통량 은 150척이었다. 4개의 통계치가 모두 중앙값이 평균값보다 작게 나타났다. 일반적으로 관측치가 균일하게 분포되어 있는 경우 중앙값과 평균값이 유사하게 나타나지만, 중앙값이 평균 값보다 작게 나타난 것은 데이터의 분포가 좌측에 치우쳐 있 음을 의미한다.
3.3 최적분포 분석 결과
선행연구에서는 항로 단면에서의 선박의 최적 통항 확률분 포에 대한 연구가 대부분이었다. 따라서 대표적인 확률분포 모형을 적용하기 어려워 경계분포, 비경계분포, 비음수분포, 고급분포로 구분된 총 31개의 확률분포를 모두 적용하였다.
최적분포를 구하기 위한 적합성 검증은 KS 검정을 사용하 였으며, 유의수준은 0.01와 0.05로 하였다.
최적분포를 구하기 위해서 Mathwave사의 EasyFit Progressional Version 5.6을 사용하였으며, 적합성 검증 결과 에 따른 최적분포 상위 3개의 분포를 구하였다.
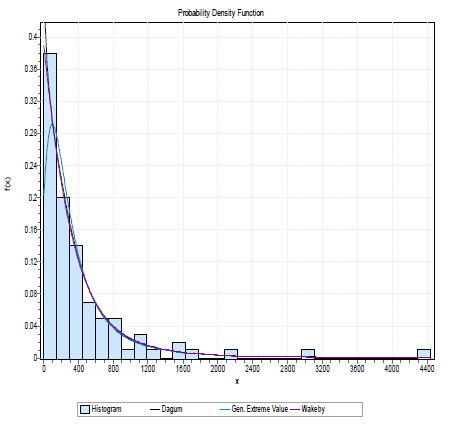
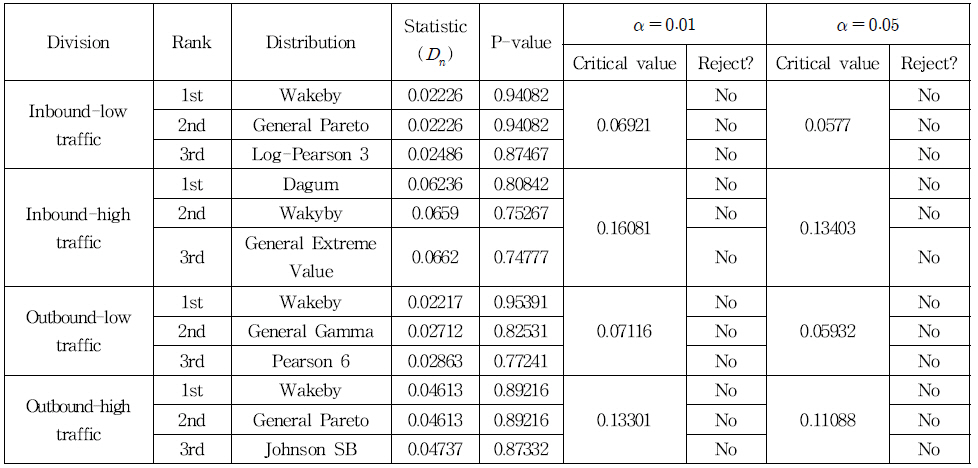
Table 4는 31개의 확률분포 중 입출항 구분, 교통량의 구분 에 따른 최적분포 상위 3개의 적합성 검증 결과이고, Fig. 7은 입항시 높은 교통량에 대한 적합성 검증에 따른 상위 3개의 적합성 검증 결과 그래프이다.
부산 북항 제1항로에서 입항시 높은 교통량에서는 Dagum 확률분포가 최적 확률분포로 분석되었으며 다른 경우에서는 모두 Wakeby 확률분포가 최적 확률분포로 분석되었다. 최적 분포 상위 3개의 확률분포 모두 유의수준 0.01과 0.05에서 모 두 유의한 것으로 분석되었다.
상위 3개의 분포는 Wakeby, General pareto, Log-pearson 3, General extreme value와 같이 고급분포가 다수를 차지하 였고, Dagum, General Gamma, Pearson 6와 같이 비음수 함 수가 그 다음 많았으며, Johnson SB와 같이 경계분포도 있었 지만, 비경계분포는 없는 것으로 분석되었다.
이는 도로교통에서 차두시간 분포를 결정하기 위하여 Zhang et al.(2007)과 Moon and Kim(2014) 등이 비음수 함수인 Gamma, Erlang, Log-normal 분포를 사용하여 적합성을 검증 한 것과 그 결과가 다른 것으로 분석되었다.
따라서 향후 항로 통항 선박간의 시간분포를 적용함에 있어 서 도로교통 등의 선행연구에서 사용한 대표적인 확률분포를 그대로 적용하는 것은 적합하지 않는 것으로 판단된다.
3.4 최적 확률분포를 이용한 통항 선박간 거리 추정 결과
부산항 북항 제1항로에서의 선박간의 통항 시간분포에 따 라 통항 선박간의 거리를 추정할 수 있다.
우선 교통조사 자료를 바탕으로 목표선을 통과한 선박간 의 거리는 식(8)에 의해 구하였다.
여기서 t1은 연속하여 통항하는 선박 중 앞선 선박이 목표 선을 통과한 시각, t2는 연속하여 통항하는 선박 중 뒤따르는 선박이 목표선을 통과한 시각, V2는 뒤따르는 선박의 속력이 며, 단 t1에서 t2까지 V2의 변화는 없다고 가정하였다.
이렇게 구해진 D 값의 중간값을 구하였다.
최적 확률분포로 선정된 Wakeby를 이용하여 중간값, 즉 확률 50%에 해당하는 통항 선박간의 시간 간격을 구하고, 여 기에 부산항 북항 제1항로의 제한 속력인 10knots를 적용하 여 통항 선박간의 거리 간격을 추정하였다.
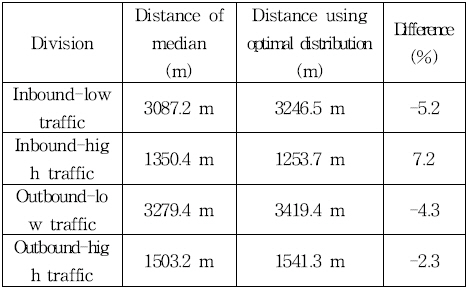
Table 5는 교통조사 자료시 관측한 목표선을 통과한 선박 간의 거리 간격의 중간값과 최적 확률분포를 이용한 통항 선 박간의 거리 간격의 추정값에 대한 비교 결과이다.
Table 5에서 보는 바와 같이 최적 확률분포를 이용한 값이 실제 교통조사 자료의 값과 비교하면 그 차이가 약–5.2∼ 7.2% 이내였다.
4. 결 론
항로는 선박의 통항이 빈번하고 특히, 항로의 입구부는 선 박의 출입이 잦아 해양사고의 위험이 높은 곳이다. 이에 오래 전부터 선박의 통항흐름과 교통용량 측정 등에 대한 관심이 많은 구역이었다.
선행 연구는 주로 항로 폭을 기준으로 단면에서의 통항 확률 분포에만 초점을 맞춘 연구가 다수였으며, 항로를 통항하는 선 박의 통항 시간간격에 대한 연구는 부족하다는 한계가 있었다.
이에 본 연구에서는 우리나라의 대표적인 항로인 부산 북 항 제1항로를 대상항로를 선정하여 항로 통항 선박의 시간 최적 확률분포에 대하여 연구하였다.
우선 대상항로의 1주일간의 교통현황 조사를 시행하였으며, 그 자료를 바탕으로 항로 입구부에 1개의 Gate line을 설정하 였다. 해상교통 분석 자료를 바탕으로 입출항과 교통량을 구분 하여 항로 통항 선박간의 시간 최적 확률분포를 분석하였다.
우선 선박간의 시간 최적 통항 확률분포를 분석하기 위하 여 단일 확률분포를 경계분포, 비경계분포, 비음수분포, 고급 분포로 구분하여 총 31개 확률분포를 적용하였으며, 최적 확 률분포 상위 3개를 분석하기 위하여 KS 검정을 사용하였다.
대상항로에서의 통항 선박간의 최적 시간 확률분포는 Wakeby 분포로 분석되었으며, 도로교통 등의 선행연구에서 사용한 비음수 분포와는 다르게 고급분포가 대부분을 차지하 는 것으로 분석되었다. 따라서 향후 항로 통항 선박간의 시간 분포를 적용함에 있어서는 다른 교통 분야의 선행연구에서 사용한 대표적인 확률분포를 적용하는 것은 적합하지 않은 것으로 판단된다.
이렇게 구하여진 최적 확률분포를 이용하여 통항 선박간 의 거리를 추정한 값과 실제 교통조사 시 구한 통항 선박간 의 거리간격을 비교한 결과 약–5.2∼7.2%내외의 오차로 비 교적 유의미한 결과로 해석할 수 있었다.
이 연구의 성과는 다음과 같이 정리할 수 있다.
첫째, 선행 연구에서는 항로 폭을 기준으로 항로 단면에서 의 선박의 통항 움직임 확률분포를 이용하여 분석하였다면, 본 연구에서는 항로 통항 선박간의 시간 간격을 확률분포로 분석하였고, 다른 교통 분야의 선행 연구 등에서 적용한 대표 적인 확률분포가 통항 선박간의 최적 시간 확률분포로 사용 하기에는 적합하지 않다는 것을 알 수 있었다.
둘째, 항로 통항 선박간의 시간간격에 대한 확률분포를 입 출항, 선박의 교통량으로 구분하여 분석하였으며, 향후 항로 에서 통항 선박의 교통용량 산정 및 안전 이격거리 평가 등 항로에서의 교통 혼잡과 안전성 측면에서 유용하게 활용될 것으로 판단된다.
다만 본 연구는 부산 북항 제1항로를 대상으로 한정된 연 구인만큼 향후 보다 다양한 환경에서의 항로 통항 선박간의 시간간격 및 교통용량 산정 등의 후속 연구가 필요할 것으로 판단된다.